Introduction

As part of our experimentation with methods for entity resolution tasks (see our publication "Meta-blocking with KLSH"), we perform an exploration of the usefulness of a feed forward network's learned representations of record features for tabular data which serve as inputs for an entity resolution clustering algorithm.

The code project is an experimental prototype for research and does not address full error handling or production standards, and it's rather a setup for quick prototyping.

In this experiment we create imaginary data that contains piano model records and we try to separate these by model according to its features.

We use a supervised siamese-like feed-forward neural network with a dual loss criterion which aims at setting entities' features apart in the representation space based on these features' embedding similarity.

We compare the clustering results of these representations to ground truth using a hierarchical clustering algorithm.

We conclude the selected rotation-invariant architecture performs well on representation reconstruction tasks but semantic representations of the entities' features results are volatile and thus inconclusive. A rethink of the network architecture can help to stand to par with machine learning methods for tabular data.

The code for this repo is available in the Github repo.

Visit here this project's github code repo DeepWiki Page structured AI-generated documentation of the code repo.

Methodology

Our approach aims at generating embeddings of record features with a neural network which will serve as inputs to a hierarchical clustering algorithm to clusters records.

We choose a siamese-like feed-forward neural network. It aims at setting entities apart in the representation space and based on the similarity of each record's feature embeddings. We calculate similarity by manipulating distance to reflect similarity.

sim_anchor_pos = torch.clamp(1 - dist_anchor_pos / margin, min=0, max=1)

We take a supervised training approach using a dual loss criterion: MSE loss on numeric and cross-entropy on category reconstructed feature values; TripletMarginLoss/ContrastiveLoss criterion on learned representation ecludean distances, albeit implicitly this helps us gauge a measure for similarity "This is used for measuring a relative similarity between samples.".

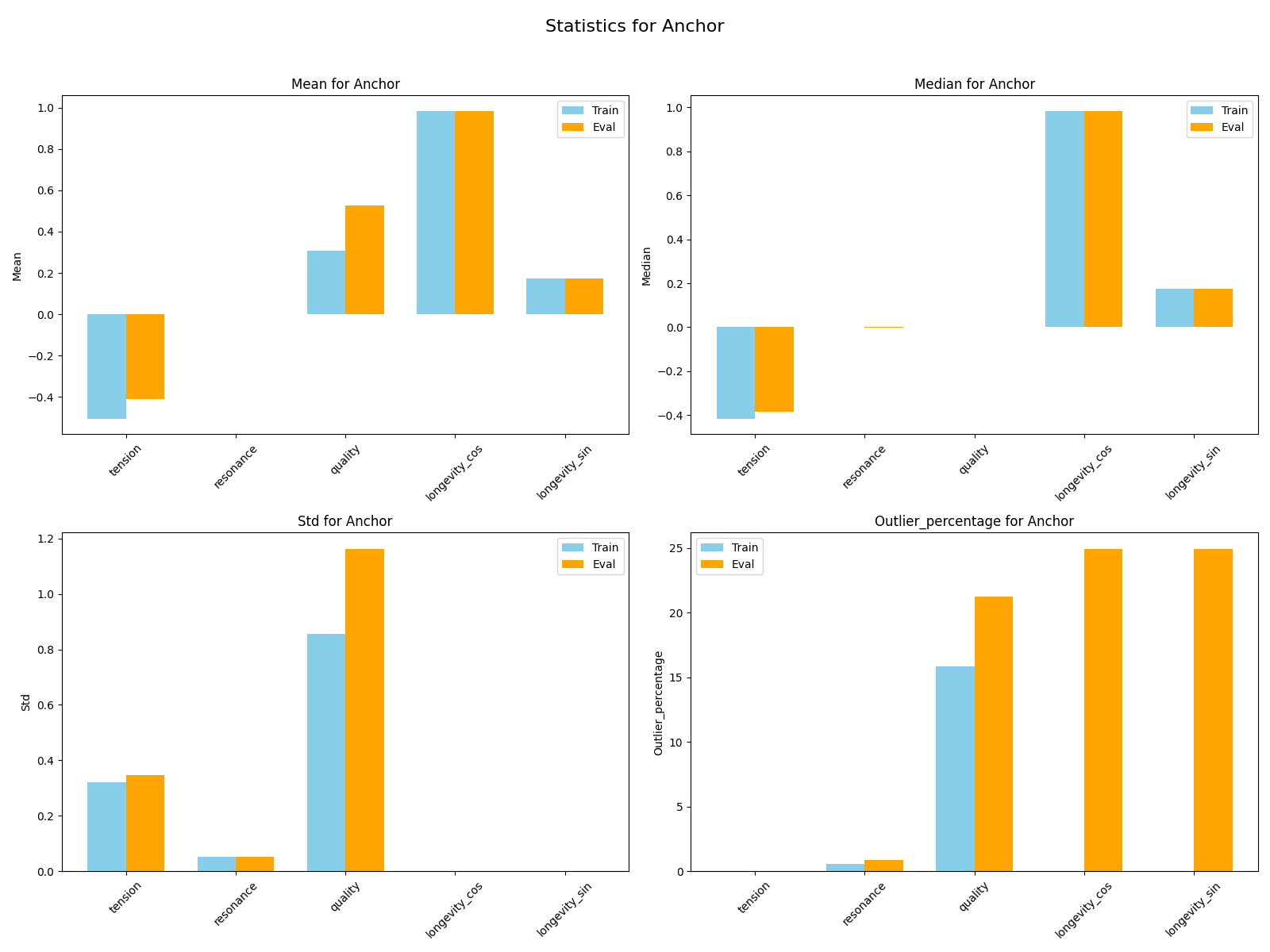
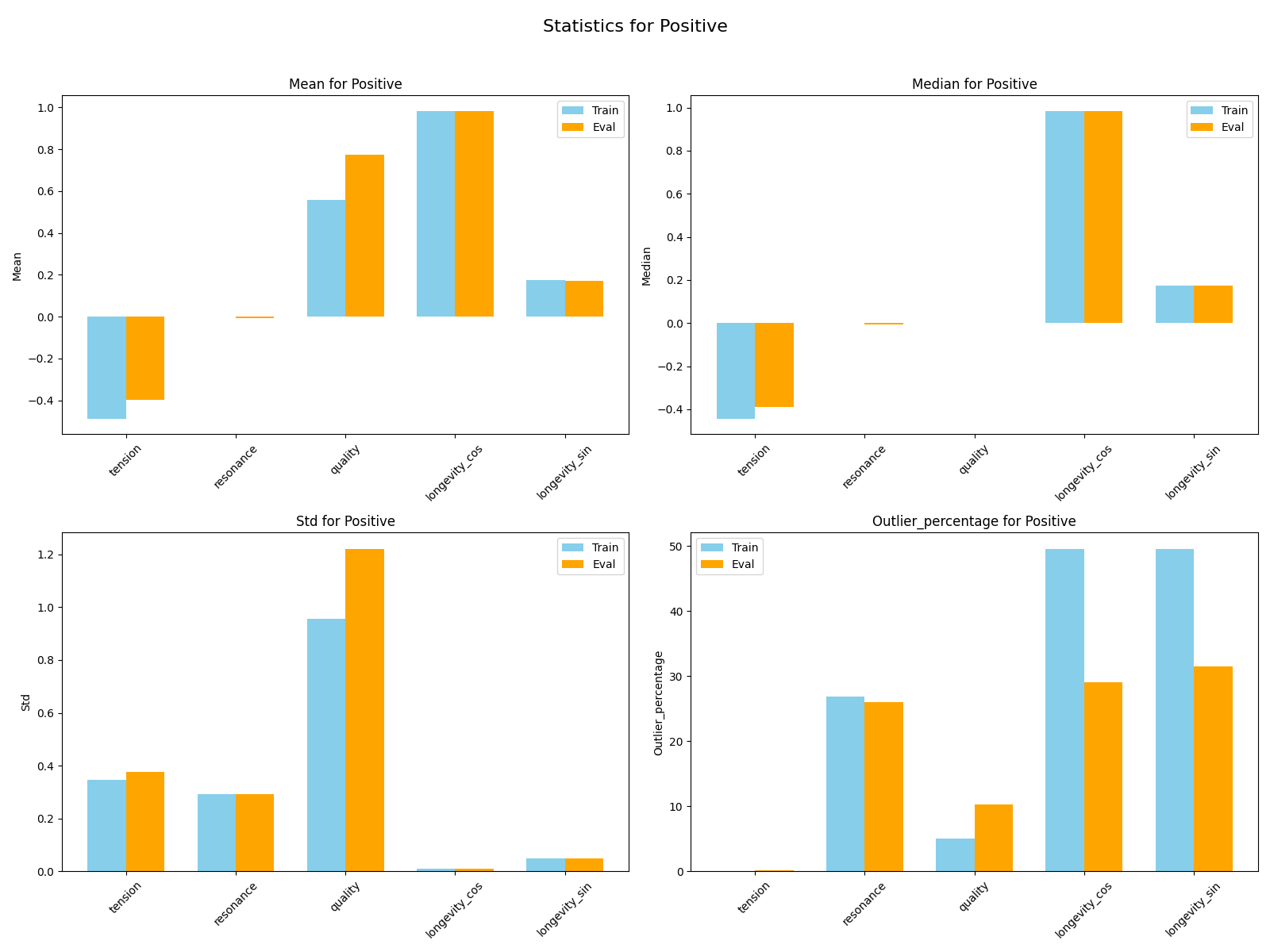
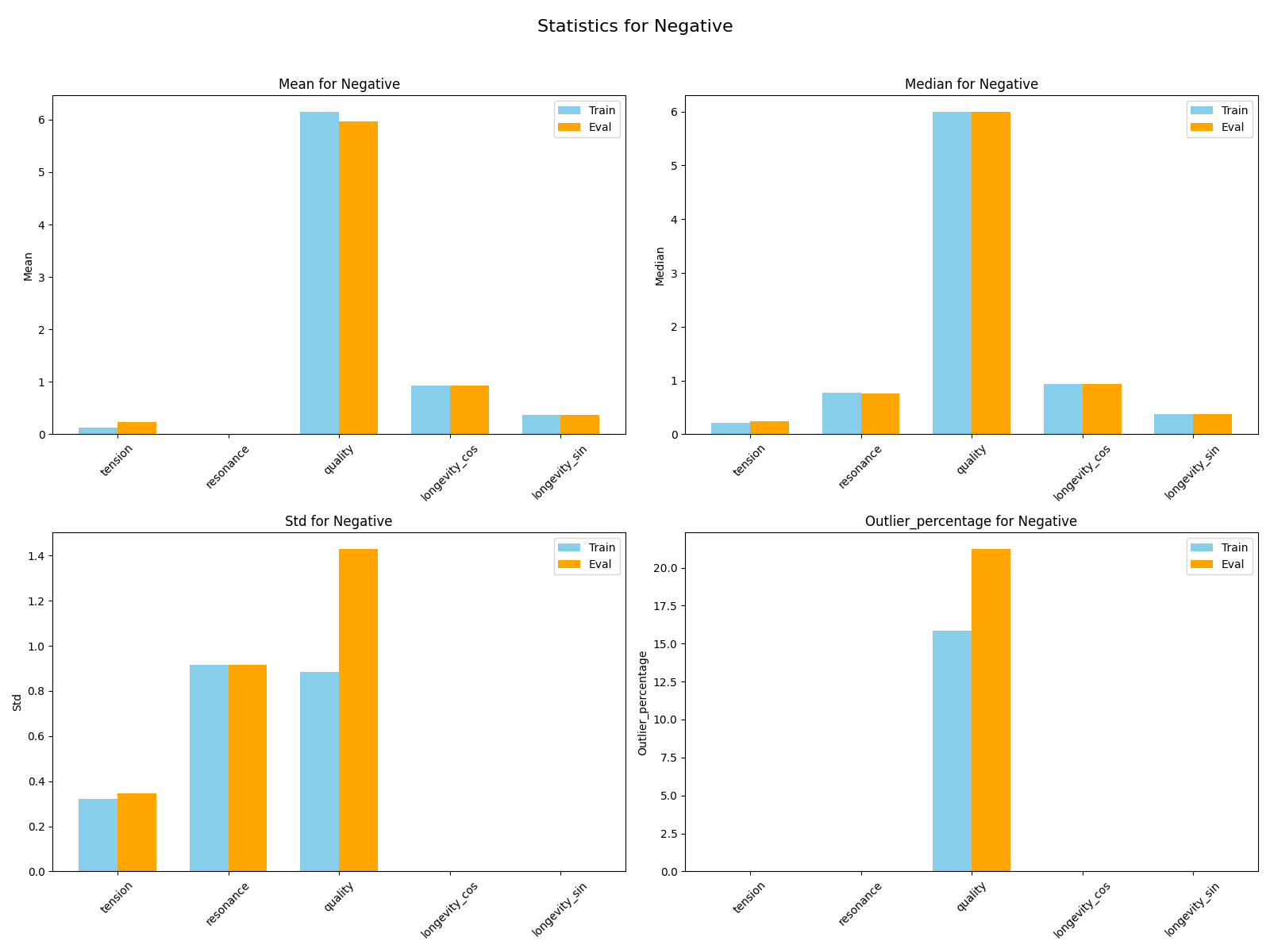
Our training and evaluation datasets contain multiple sets, referred as triplets, with three records each: an anchor or a base record; a record somewhat similar to the anchor referred as a positive, and a third dissimilar to the first two and referred as a negative. Each record is a piano model. It's therefore worth noting that an epoch trains the model and generates embeddings for each triplet record separately but with the same model and shared parameters.

We compute how far these records are represented in the embedding space and a loss is calculated by the TripletMarginLoss/ContrastiveLoss criterion which changes model gradients to get those similar closer or push apart those different subject to a margin threshold.

Based on our results and existing literature, we further refine the training approach by selecting harder records based on their distance.

We add an auxiliary reconstruction head for each feature in the network to keep track that the information for each feature in the representation space if preserved.

Finally, the resulting encoder learned representations from the model become an input to a hierarchical clustering algorithm and we compare these results to ground truth. Thus we will often refer herein to the neural network as an encoder in that it generates embedding inputs where hopefully semantically similar records are placed together in the representation space, and those different far apart.

Training and Evaluation Datasets

Both training and evaluation datasets are imaginary datasets that were created using a spreadsheet with rules to establish record dissimilarity. The training dataset counts with over 13,000 triplets or over 40,000 piano records. The evaluation dataset counts with over 2400 triplets or over 7000 records.

Feature Engineering:

Size:

• Training: 13500 triplets
• Evaluation: 2300 triplets

Features:

• Quality - Categorical: 0-9
• Resonance - Continuous
• Tension - Continuous
• Longevity - Date

Transformations:

• Category: We use the category value
• NumericContinuous: Min-Max Normalization for each feature range (-1,1) with added noise from a gaussian distribution of mean=0 std=0.05.
• Time: Date is projected to quarter circle and converts the normalized time fraction into cosine and sine values

Data rules used to generate positive and negative triplet samples:

• Positive Entity Rules: Max units away from Anchor

• Quality: 2
• Tension: 4
• Resonance: 6
• Longevity Days: 5
• Longevity Months: 2
• Longevity Years: 5

• Negative Entity Rules: Units away from Anchor

• Quality: More than 3
• Tension: More than 4
• Resonance: More than 5.3
• Longevity Days: Up to 28 days
• Longevity Months: Between 3 and 4
• Longevity Years: Betwen 6 and 10

Test dataset

Our test dataset contains 10 records which are two piano models and we aim to separate these records by model.

We use the data rules mentioned above to generate a positive and a negative record from an anchor to which we add small variations. This produces two groups of 5 records each for ground truth, one reflecting positive records and another for negative records. We expect the clustering algorithm to results in two clusters.

Enhanced Test dataset

We generate this dataset by changing one feature in record 0 of the Test dataset and add these rows (10-13) to the test dataset. Record 14 is a variation of the second piano model (quality feature is changed) in the test dataset.

Training and Evaluation Datasets distributions

Original Training and Evaluation Data Distributions:

Transformed Training Data Distributions:

Transformed Evaluation Data Distributions:

Transformed Comparison of Training and Evaluation Data Distributions:

Encoder

Siamese-like feed-forward neural network.

Loss Criterion

We apply the sum of two loss criterions to train the model.

a) Record Distance Loss:

• TripletMarginLoss using Pytorch implementation on ecludean distances based on FaceNet: A Unified Embedding for Face Recognition and Clustering where anchor-positive should be closer than anchor-negative by at least margin.

or,

• Contrastive Loss based on the Dimensionality Reduction by Learning an Invariant Mapping paper using Ecludean distances for anchor-positive and anchor-negative records and a margin.

distances = torch.norm(embedding1 - embedding2, p=2, dim=1)
loss = 0.5 * ((1-label) * distances**2 + label * torch.clamp(self.margin - distances, min=0)**2)

We experiment with the two above to observe resulting differences because Contrastive loss encourages anchor and positive samples distance to be zero while TripletMarginLoss allows for some intra-class variance for as long as a margin exists between samples of different clusters.

b) Feature Reconstruction Task:
An auxiliary loss task by reconstructing feature values from the embedding space and implemented as a regression objective: We apply a cross entropy loss on categorical features and MSE loss on numerical features.

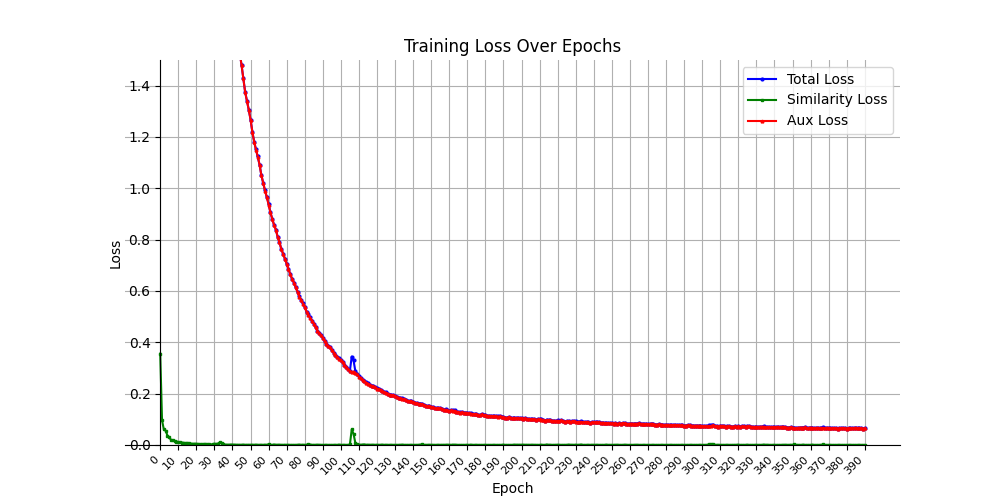
This combined loss guides the model to limit the drift of feature values in the representation space away from its actual values due to the triplets' records distance constraint. The benefits of balancing both objectives can be inferred from existing literature. We note that we observe triplet loss reaches a near zero value in the early stages of training and it's the auxiliary task that then drives embeddings for the remainder of the training epochs. Thus we also tested early stopping once the triplet loss reached ~zero.

Model Summary and Layer Architecture

The encoder's layer architecture for learned representations follows an arrow shape starting with small dimension inputs → widening middle layers → compact output. We initially expand the low-level layer dimensions, maintain the size for the high-level dimension across all features, a combined layer of the concatenated high-level layers which we expand to finally produce a more compact 128-dimensional hidden state of all input features.

This architecture counts over 200k model parameters.

Batch size

We run training and evaluation with 128 size and the dataloader shuffle enabled and disabled.

Scheduler and Optimizer

We train the model with CyclicLRWithRestarts Scheduler and thank Maksym Pyrozhok for the published open-source implementation. Its cyclic nature for learning rates and its flexible policy helped us experiment quite quickly with different architectures to exit local minima.

We combine this scheduler with the popular optim.AdamW. We follow the suggestion from existing literature that supports that AdamW weight decay can generalize better in that it is decoupled from gradient updates and hence it escapes Adam's approach where the weight decay is implicitly tied to the learning rate so changing our learning rate affects how strongly weight decay penalizes the model's weights.

Normalization

We normalize model output embeddings before loss metric calculations to maintain the stability of the model. This removes vector magnitude as a factor so distances are purely angular and the model does not minimize loss simply by increasing the norm of vectors but encode information on vector direction.

Regularization

We apply dropout = 0.3 on the early layers.
To avoid overfitting we further apply weight decay on all layers with values between 0.00001 to 0.000005, except for the combined layer 0.01 which we observe memorizes the training data.

Activation Functions

Pytorch's ReLU implementation except for LeakyReLu implementation in the tension feature reconstruction task layer to aid exploding gradients.

Similarity

We calculate the similarities by transforming the ecludean distance as in inversely scaling this distance relative to the triplet loss margin, which we then normalize to ∈[0, 1].

sim_anchor_pos = torch.clamp(1 - dist_anchor_pos / margin, min=0, max=1)

So that,

• When distance = 0: similarity = 1 (identical embeddings)
• When distance = margin: similarity = 0 (completely dissimilar)
• When distance > margin: similarity = 0 (we clamp)

Experiments

Experiment 1: Contrastive Loss

Encoder Layer Architecture Without Layer Normalization

We train the model applying ContrastiveLoss criterion using

• Ecludean distance
• margin = 2
• combined sum loss of both the Contrastive Loss and Auxiliary loss
• cyclicLRWithRestarts_restart_period = 5
• Most layers LR = 0.001
• Dataloader shuffle disabled

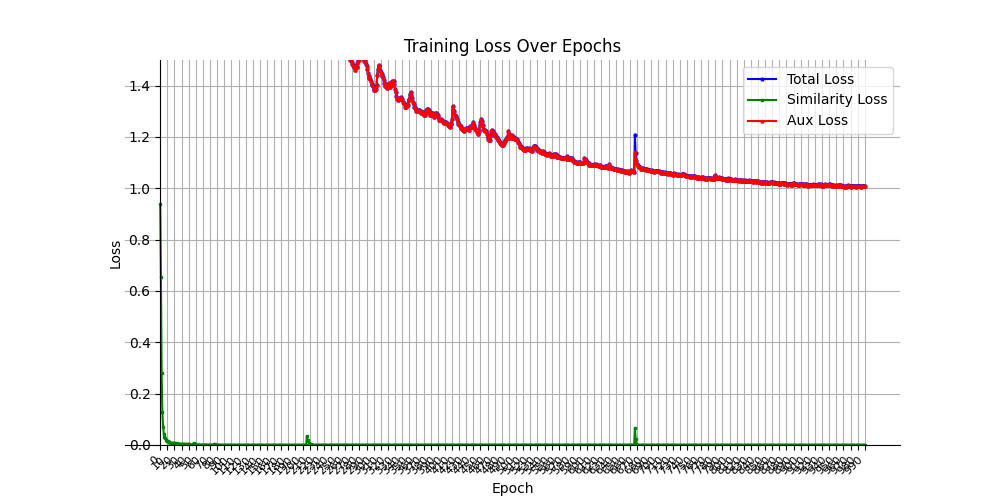
Training loss converges relatively quickly. We help the model extend triplet record distance loss training to separate records by setting Margin=2.

Anchor-positive separation from anchor-negative results:
To generate this pyplot histogram we parametrize density=True (density=1), 50 bins and equal bin width (1/50=0.02), thus max sum of heights=50.

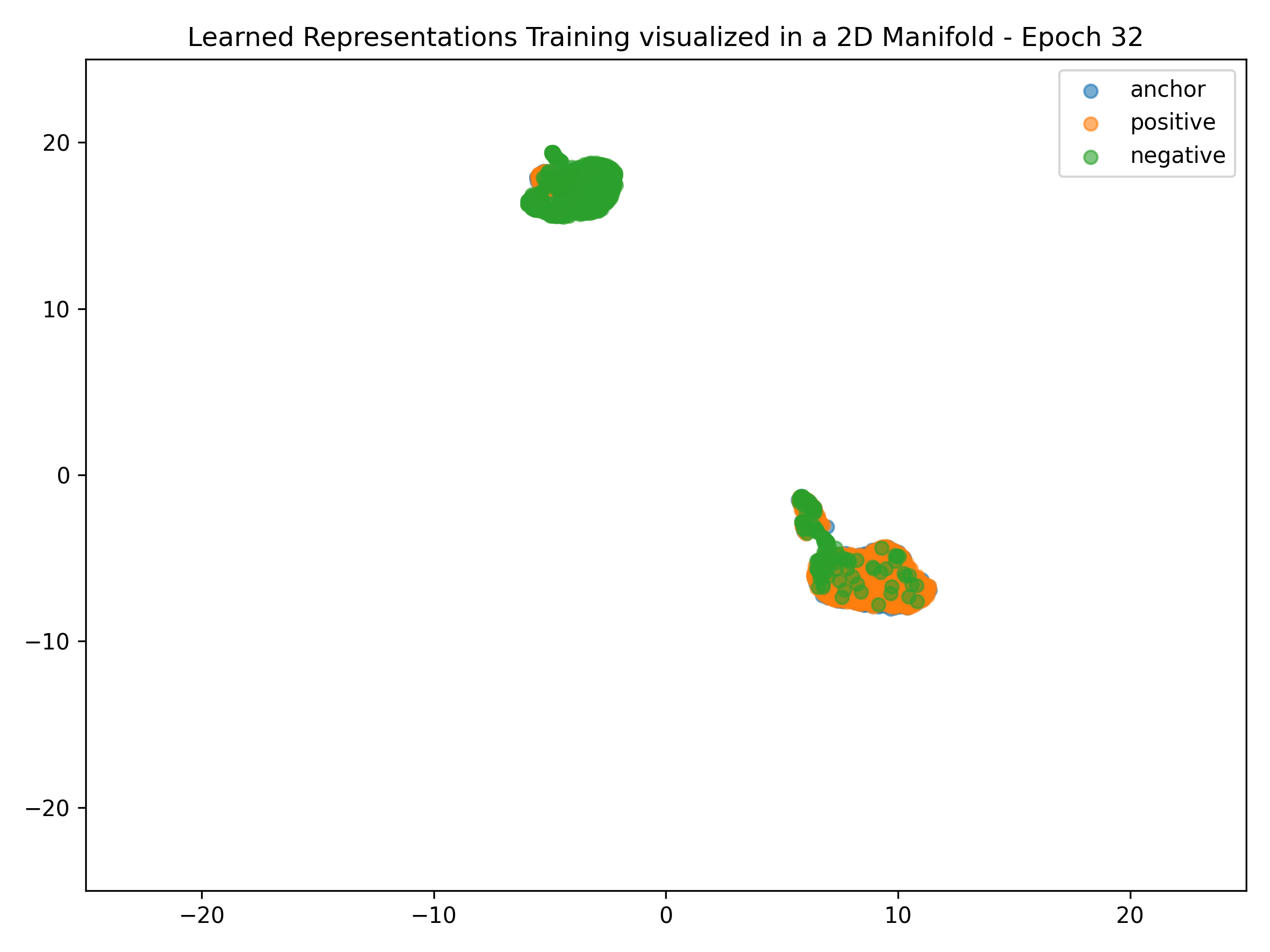
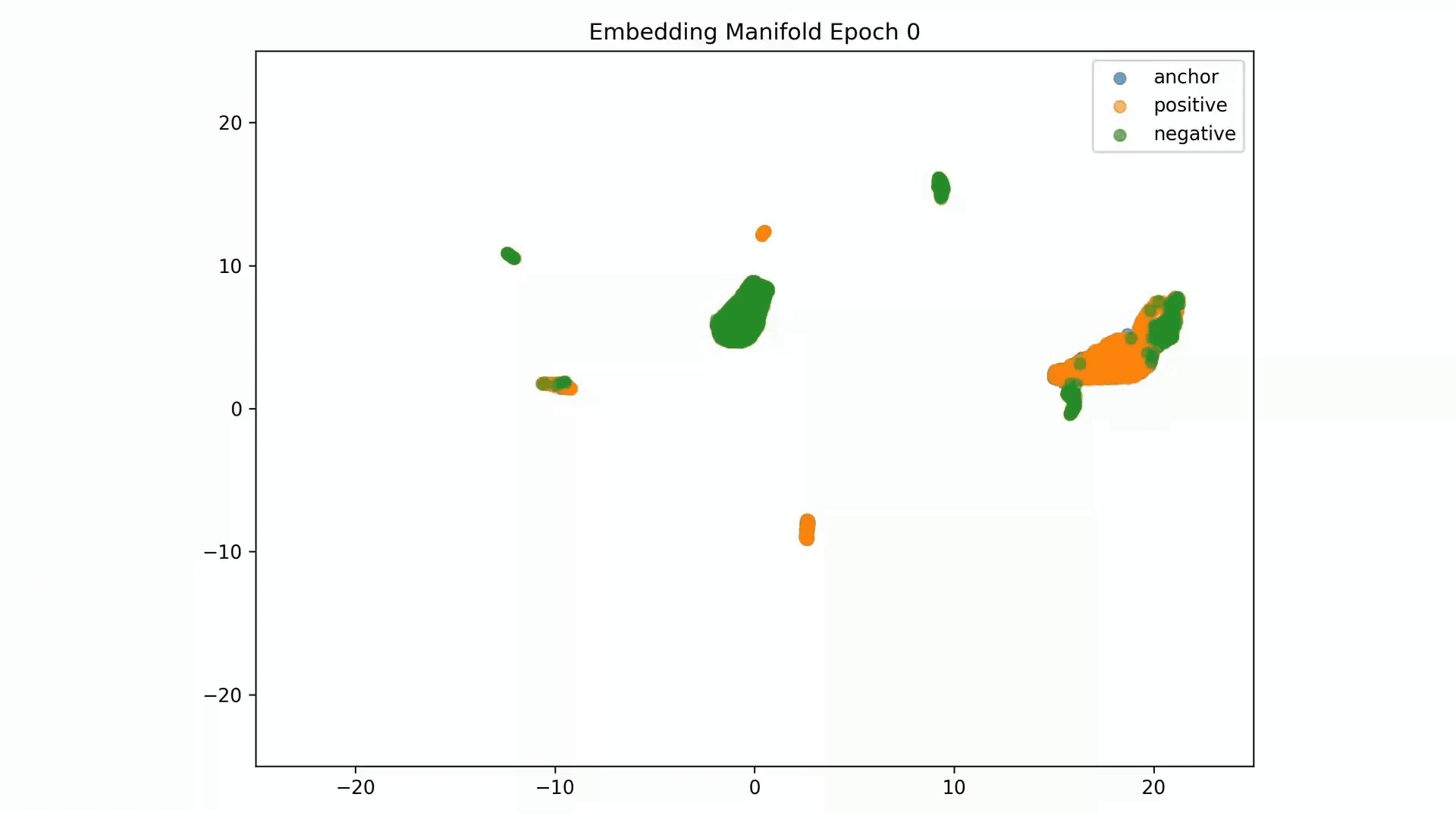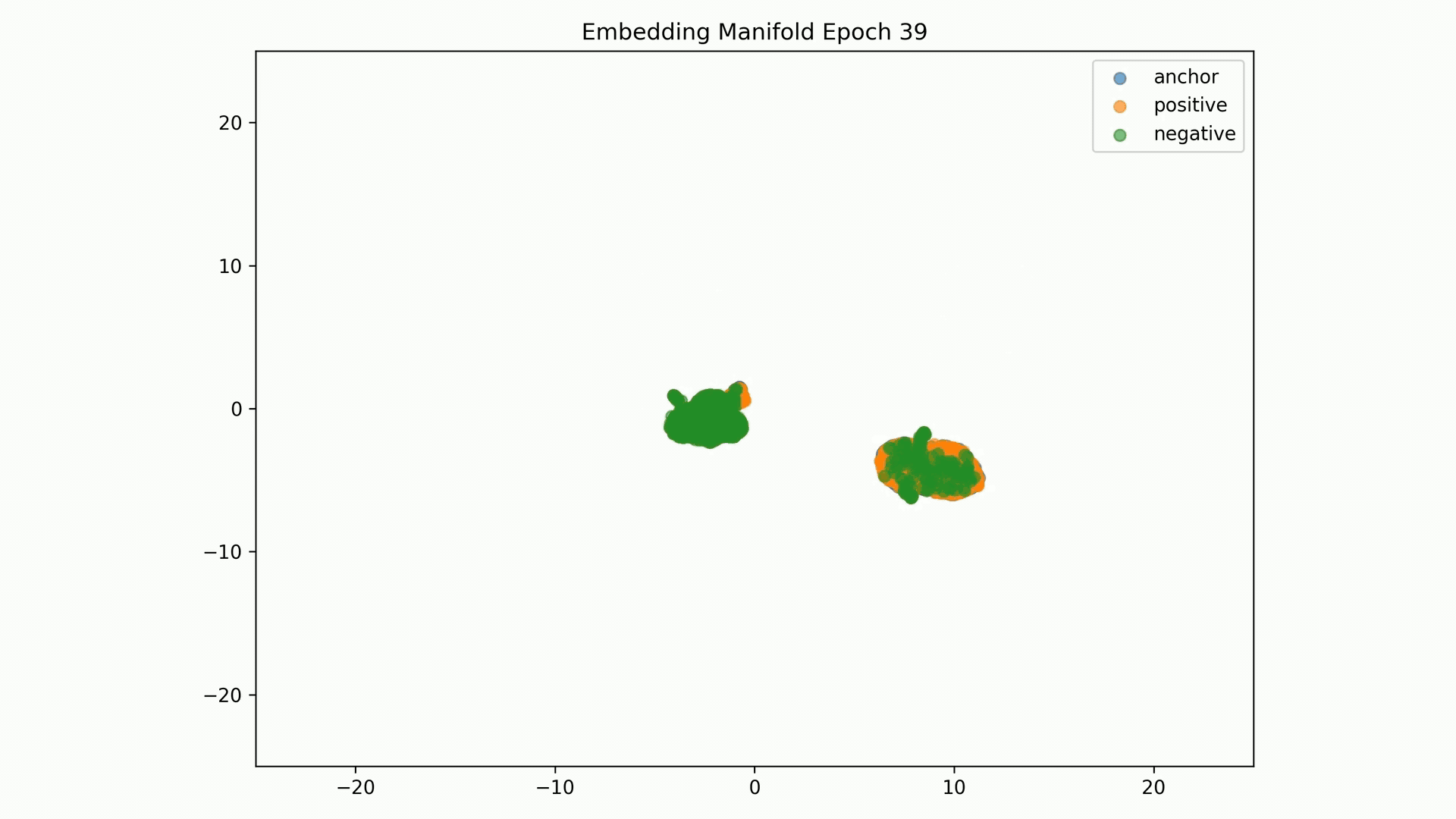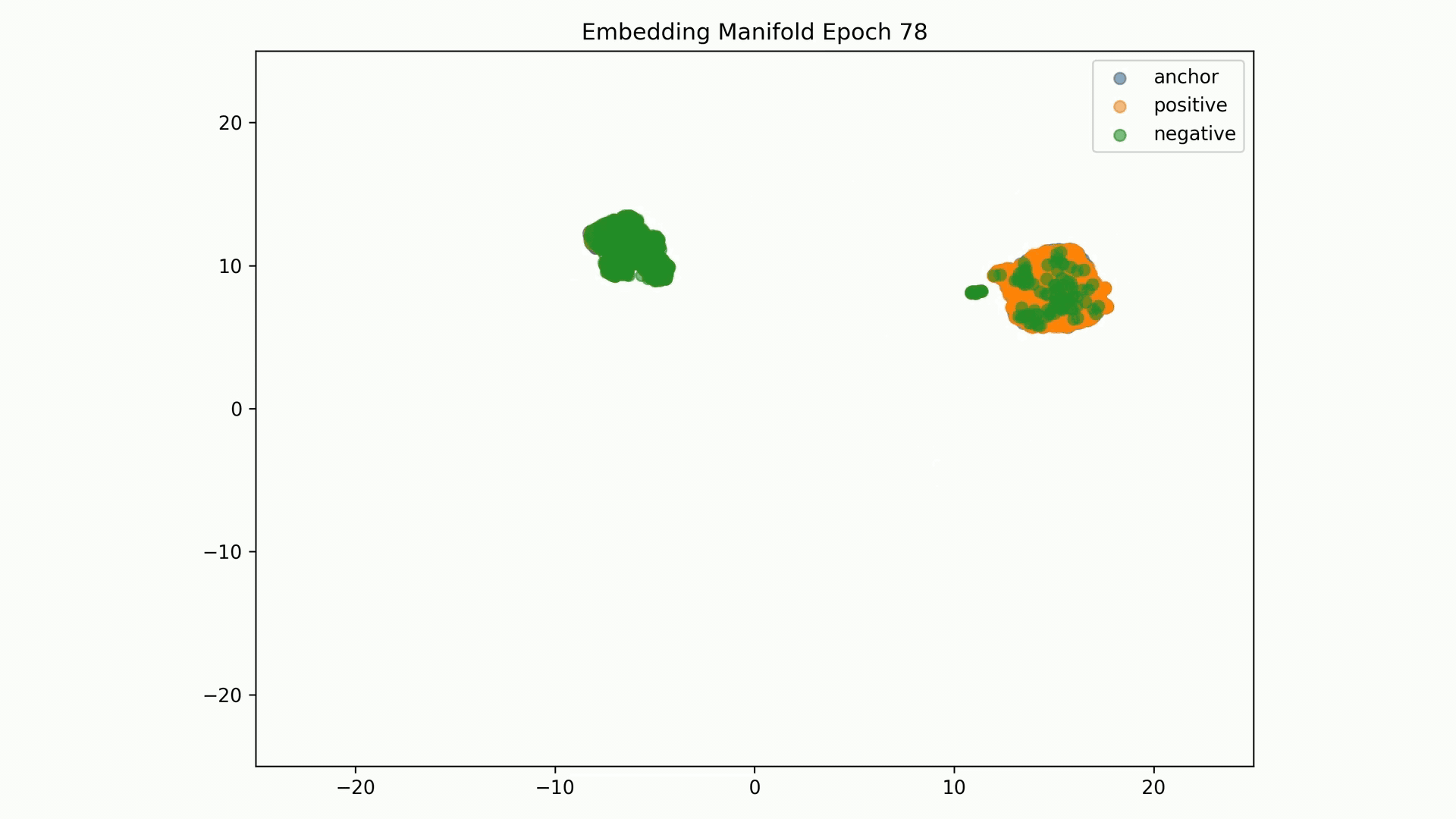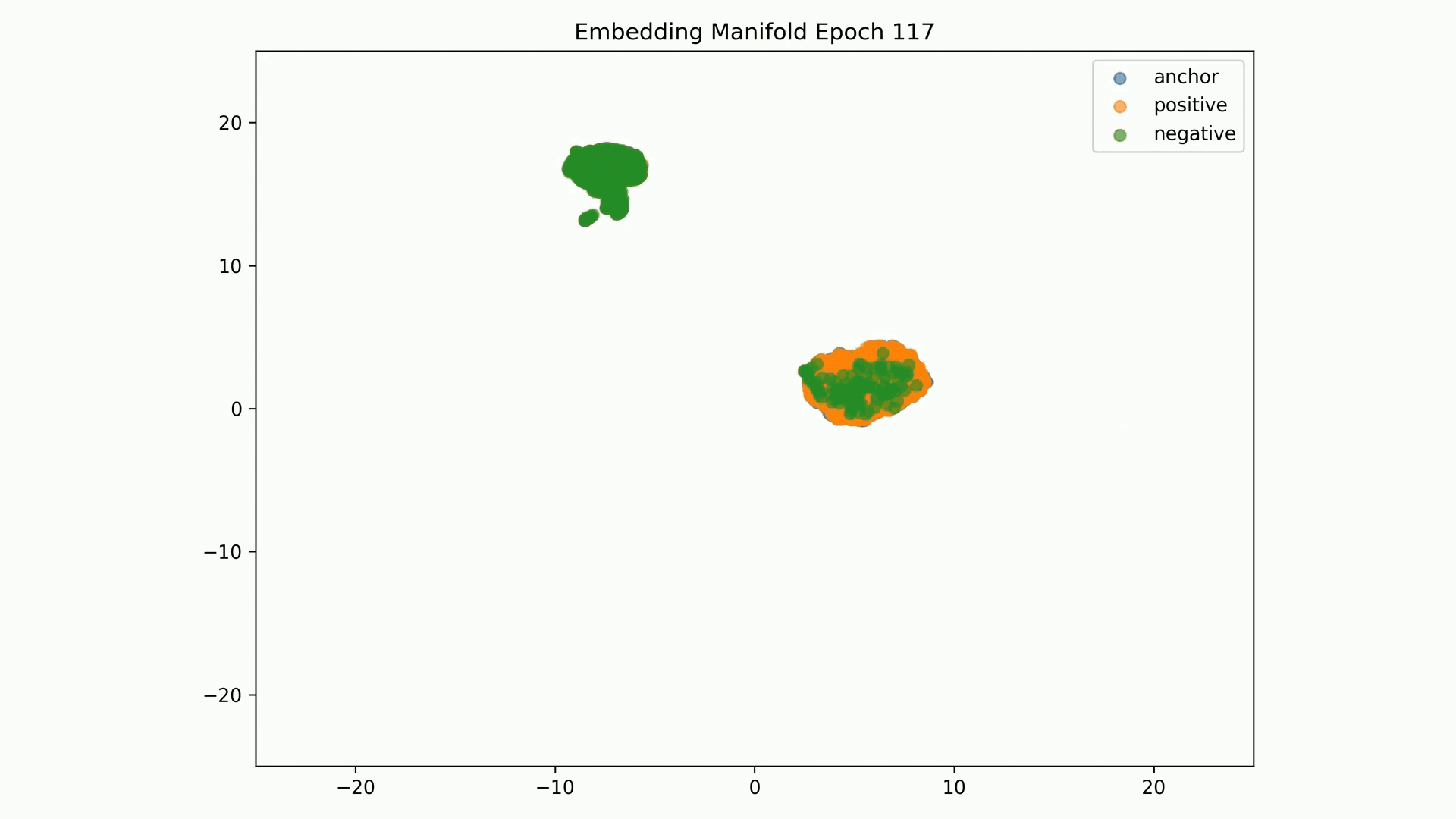
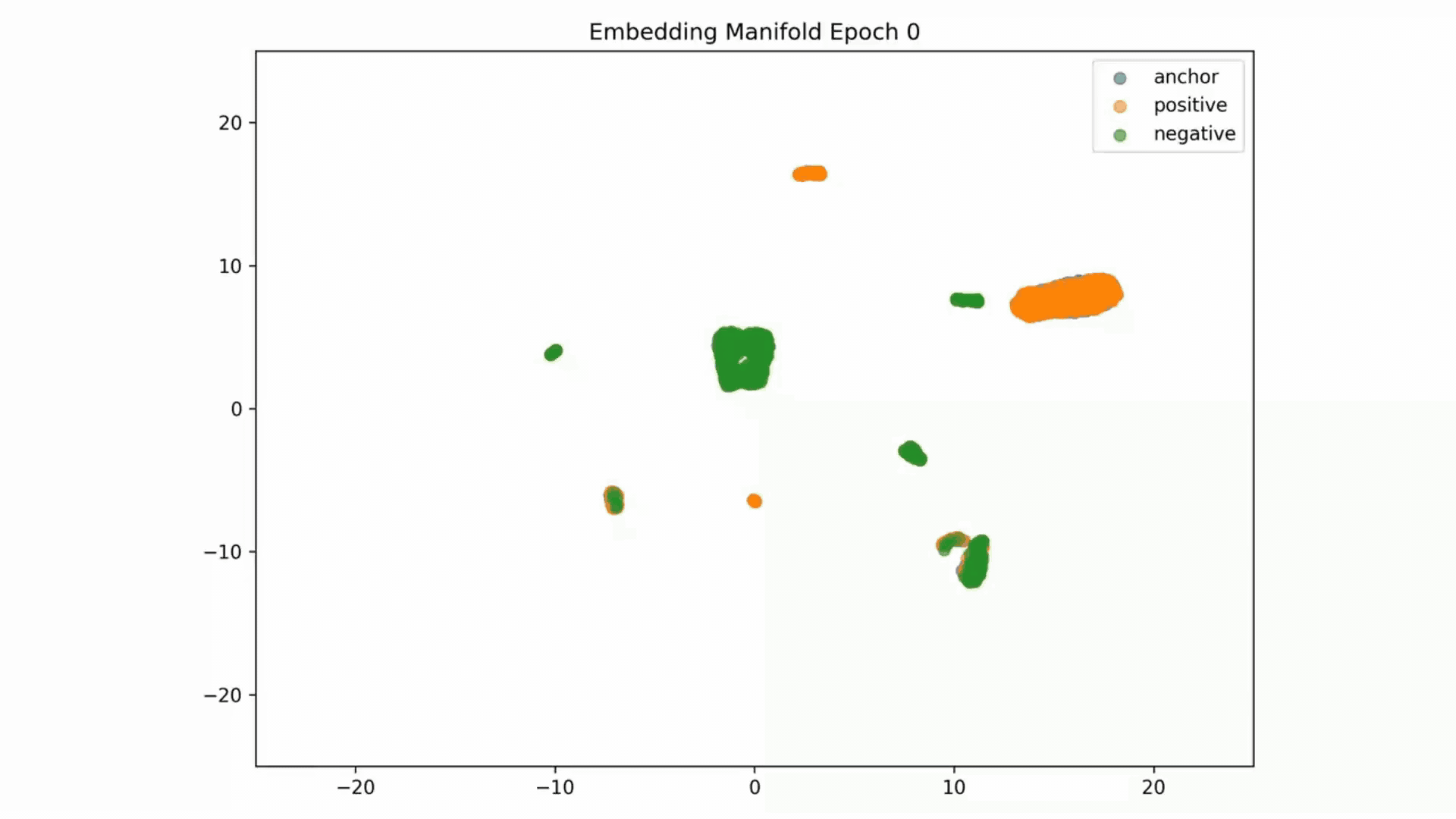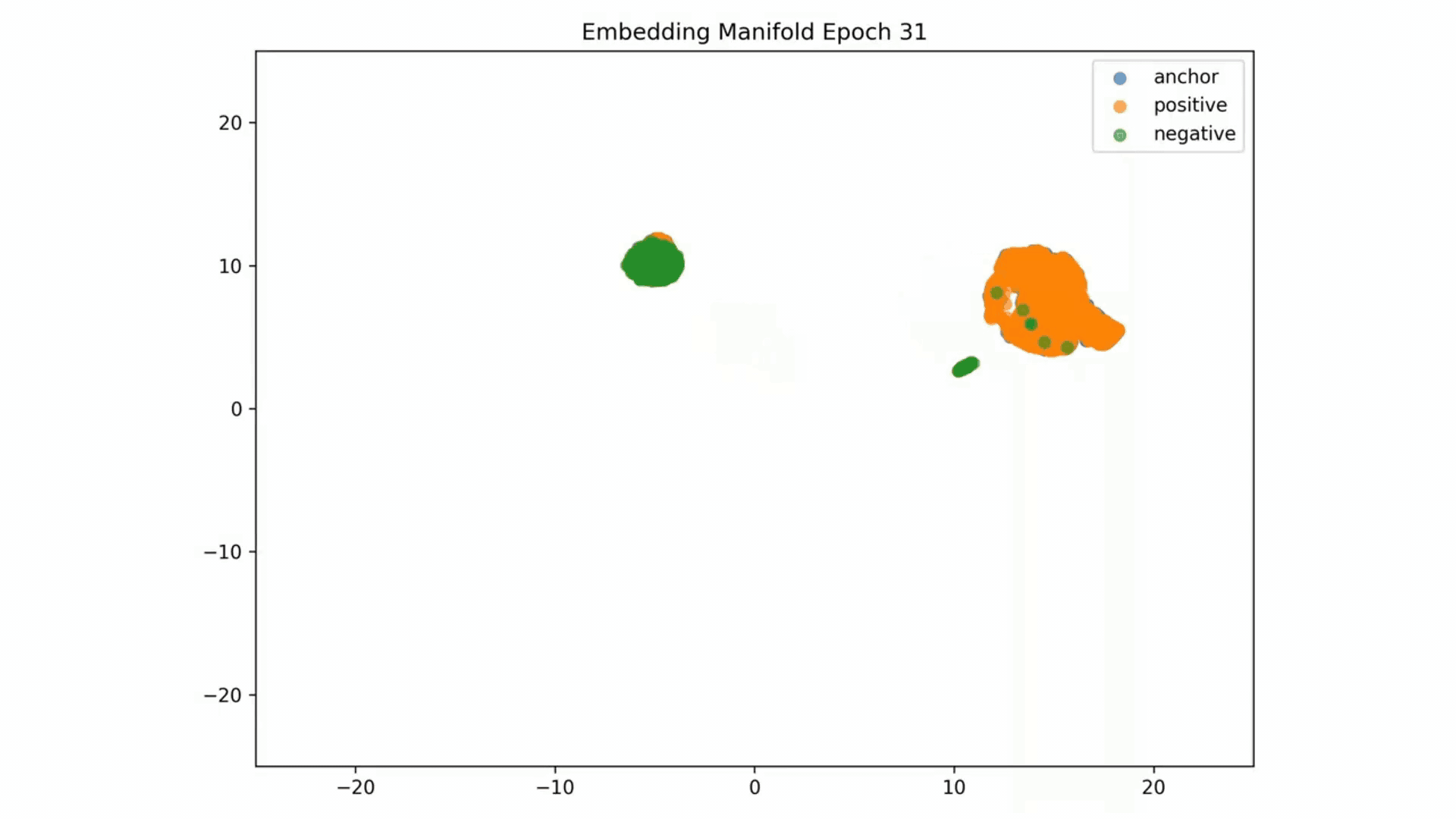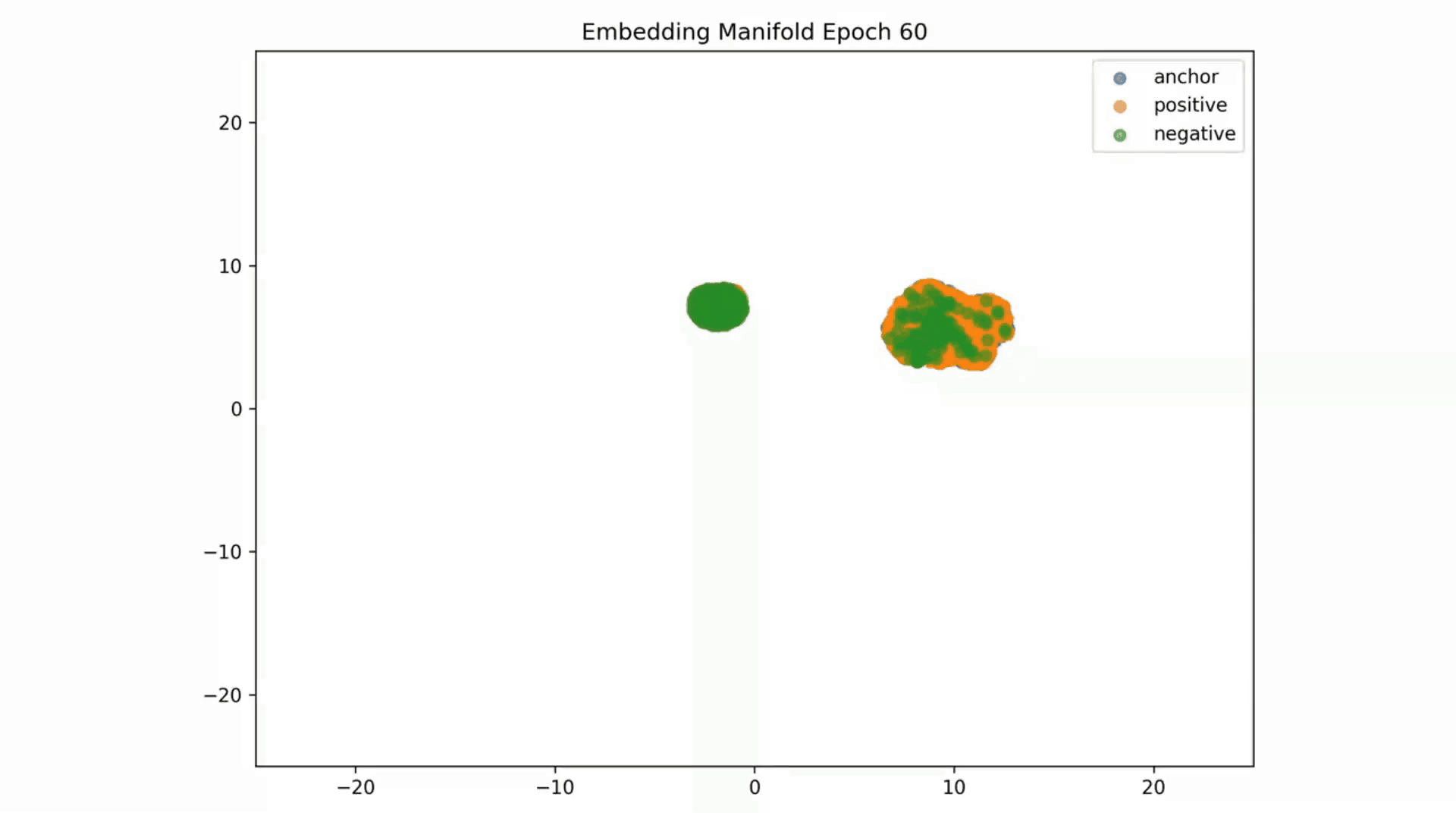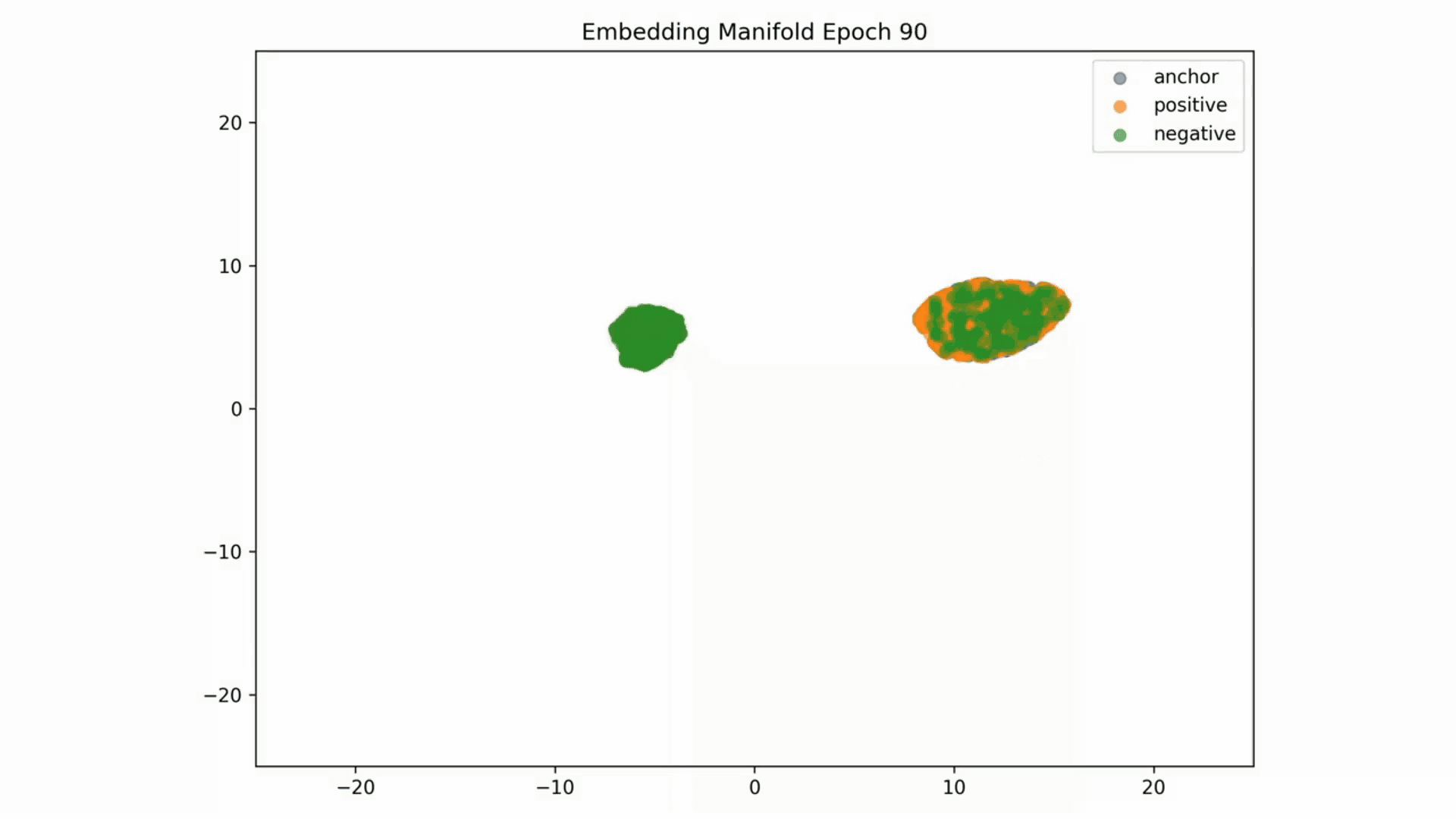
Embedding Representations Training Evolution visualized in a 2D Manifold: You can see the full training evolution here

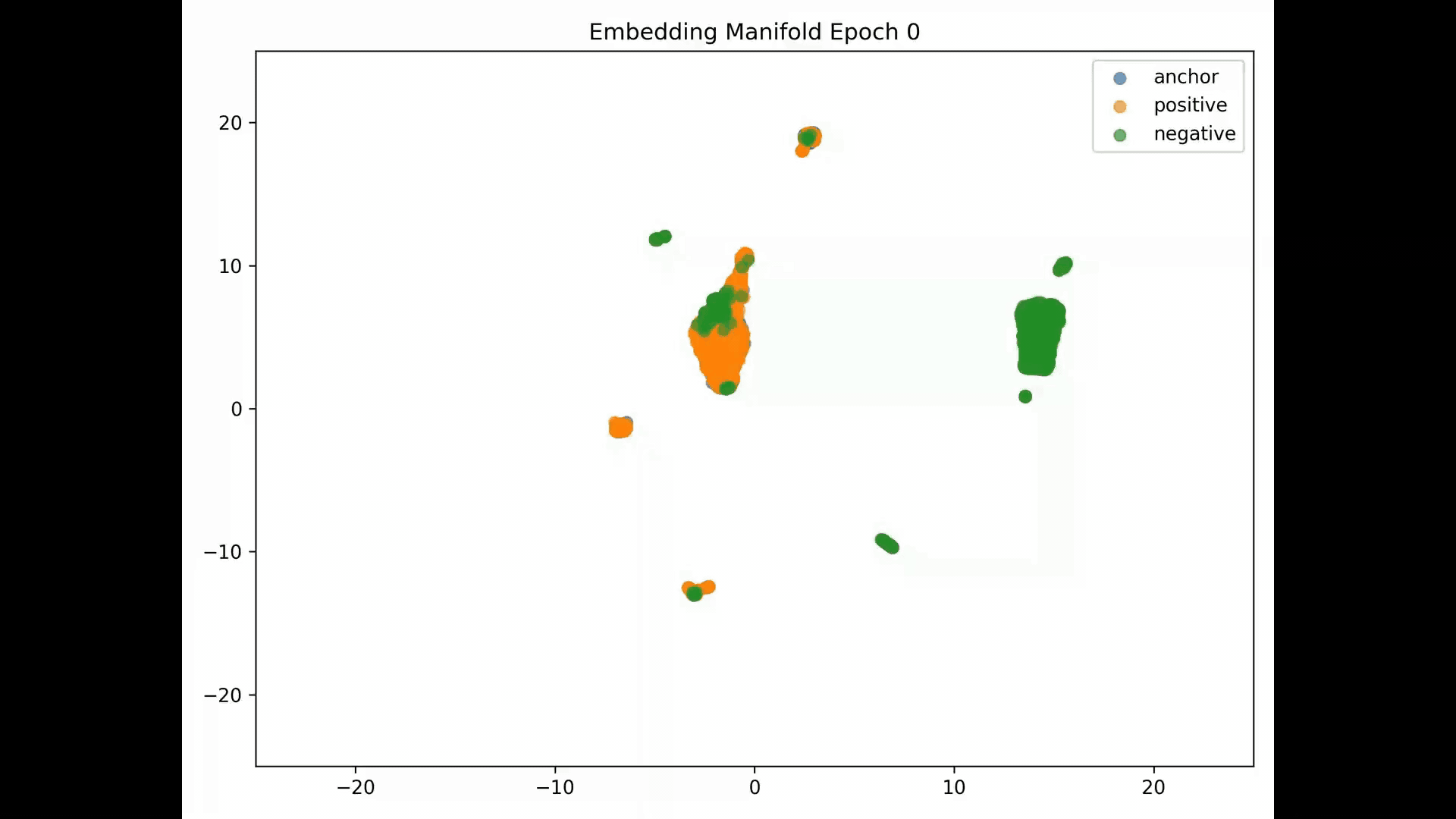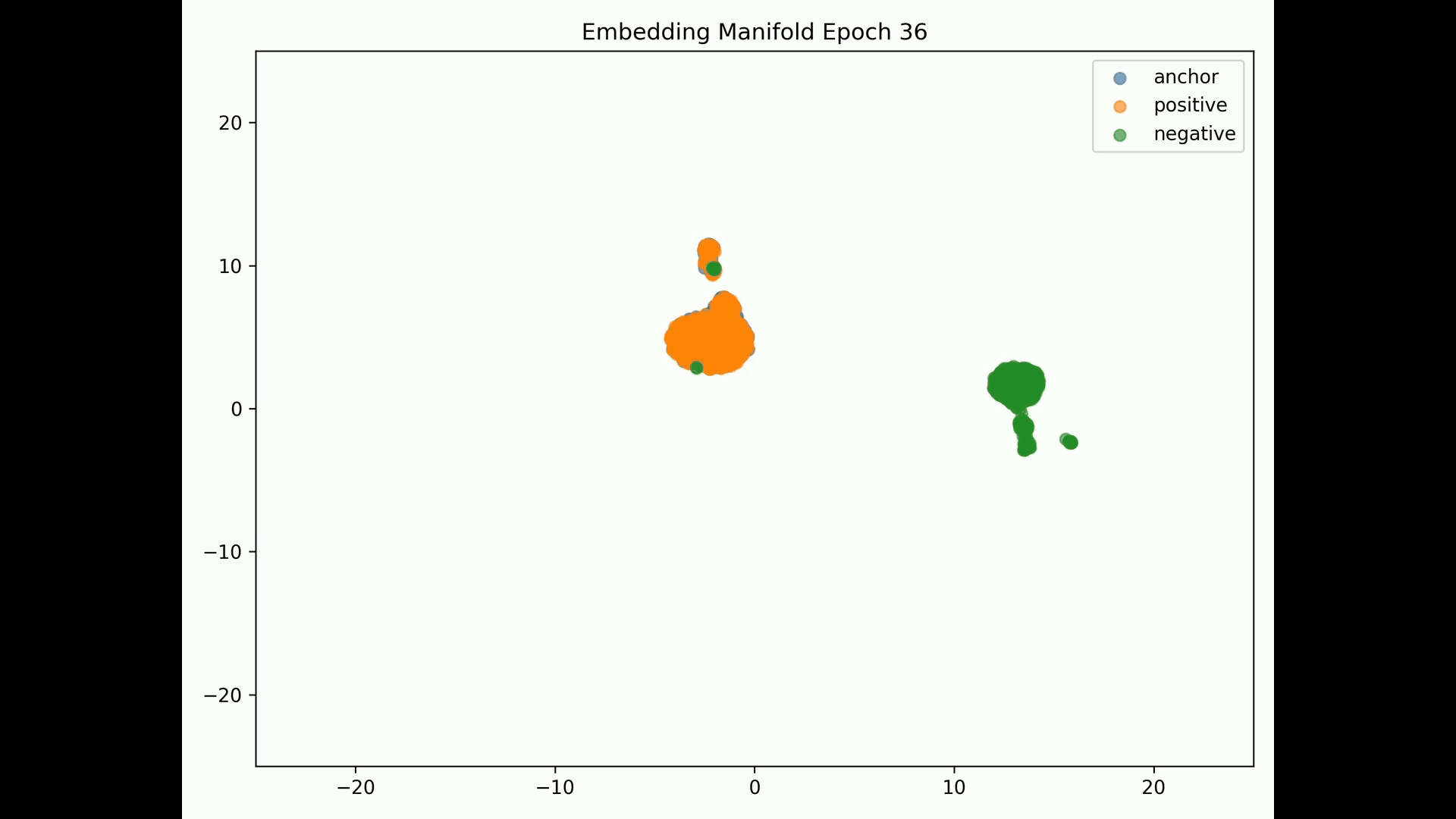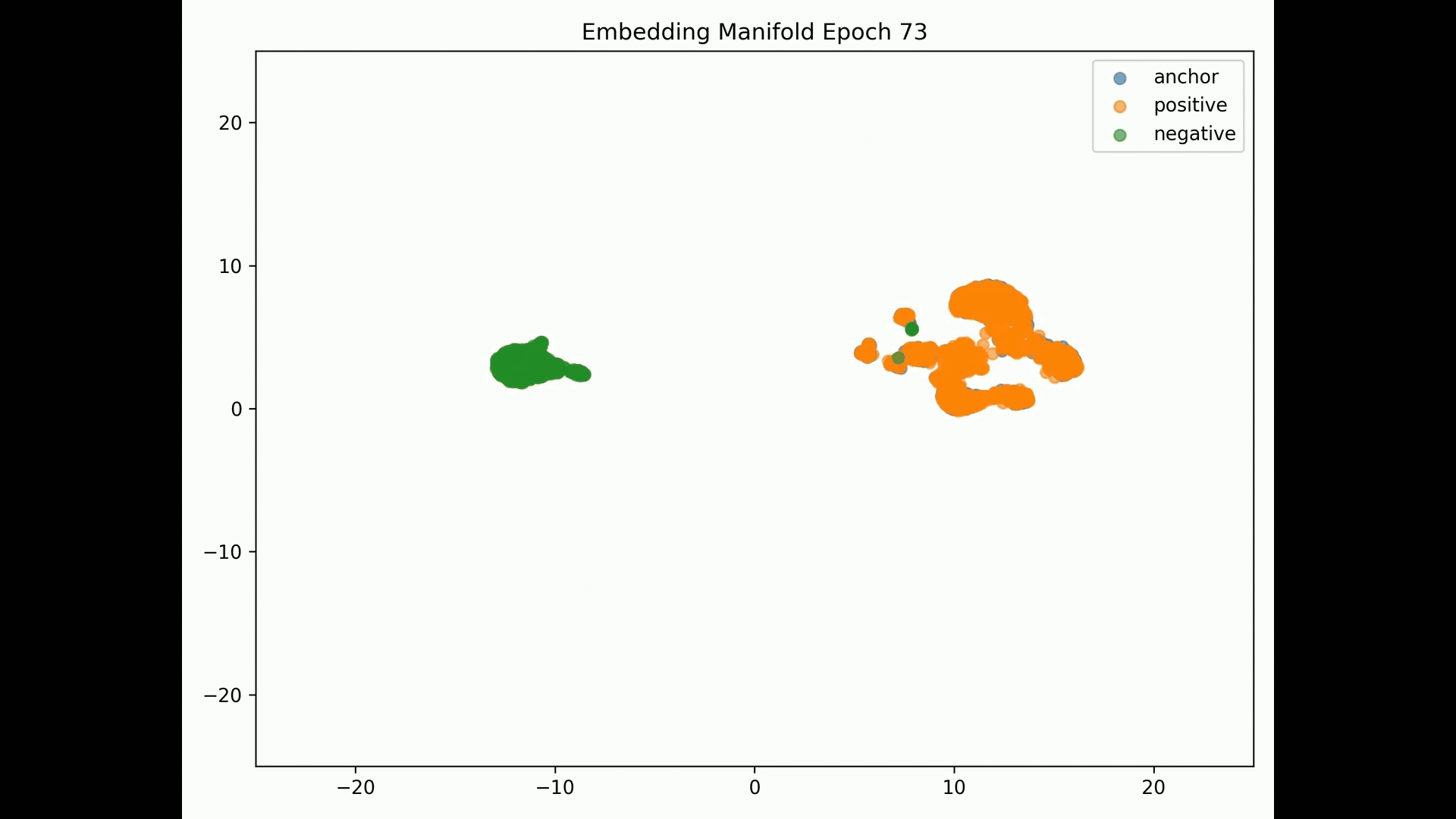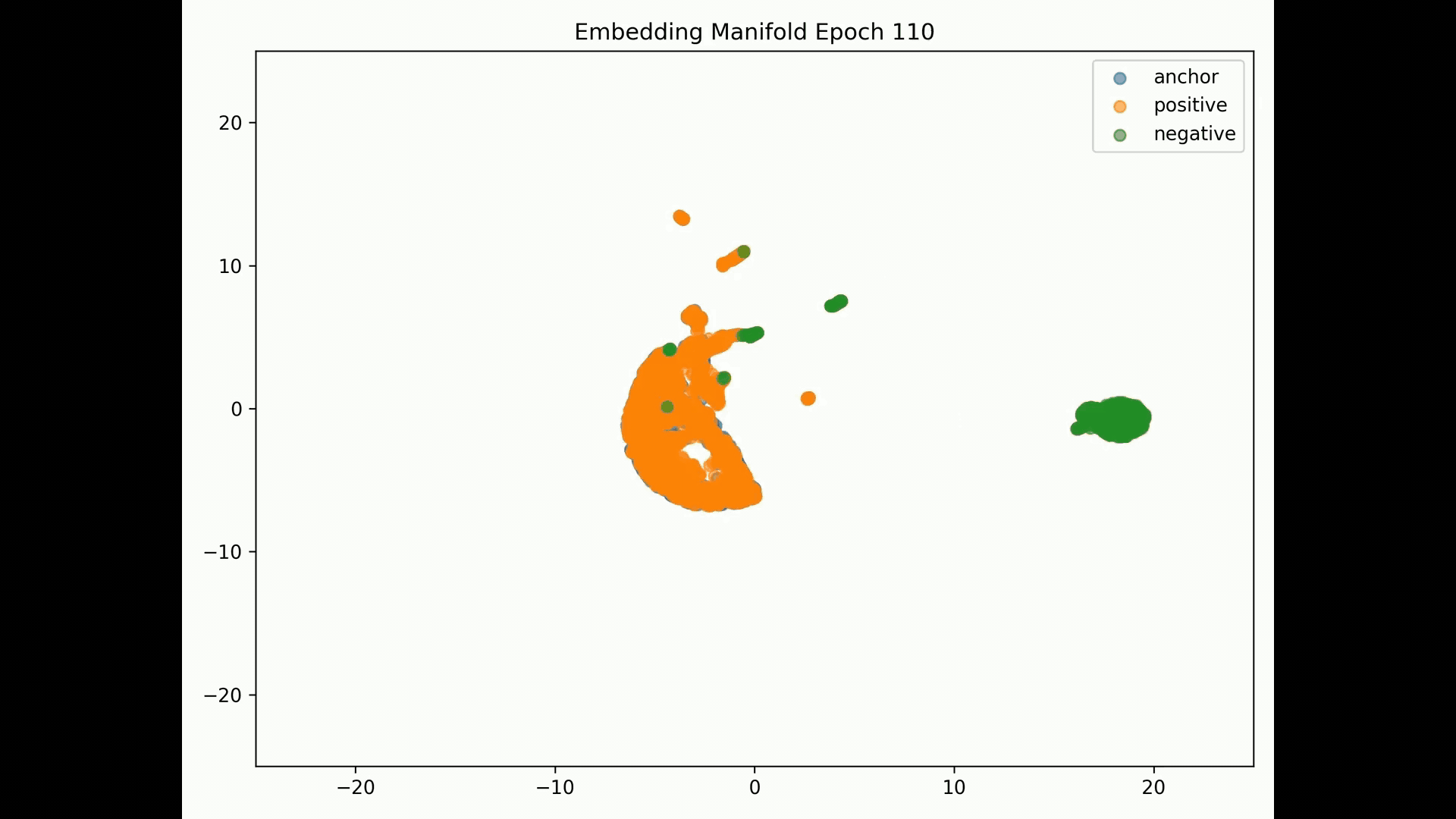
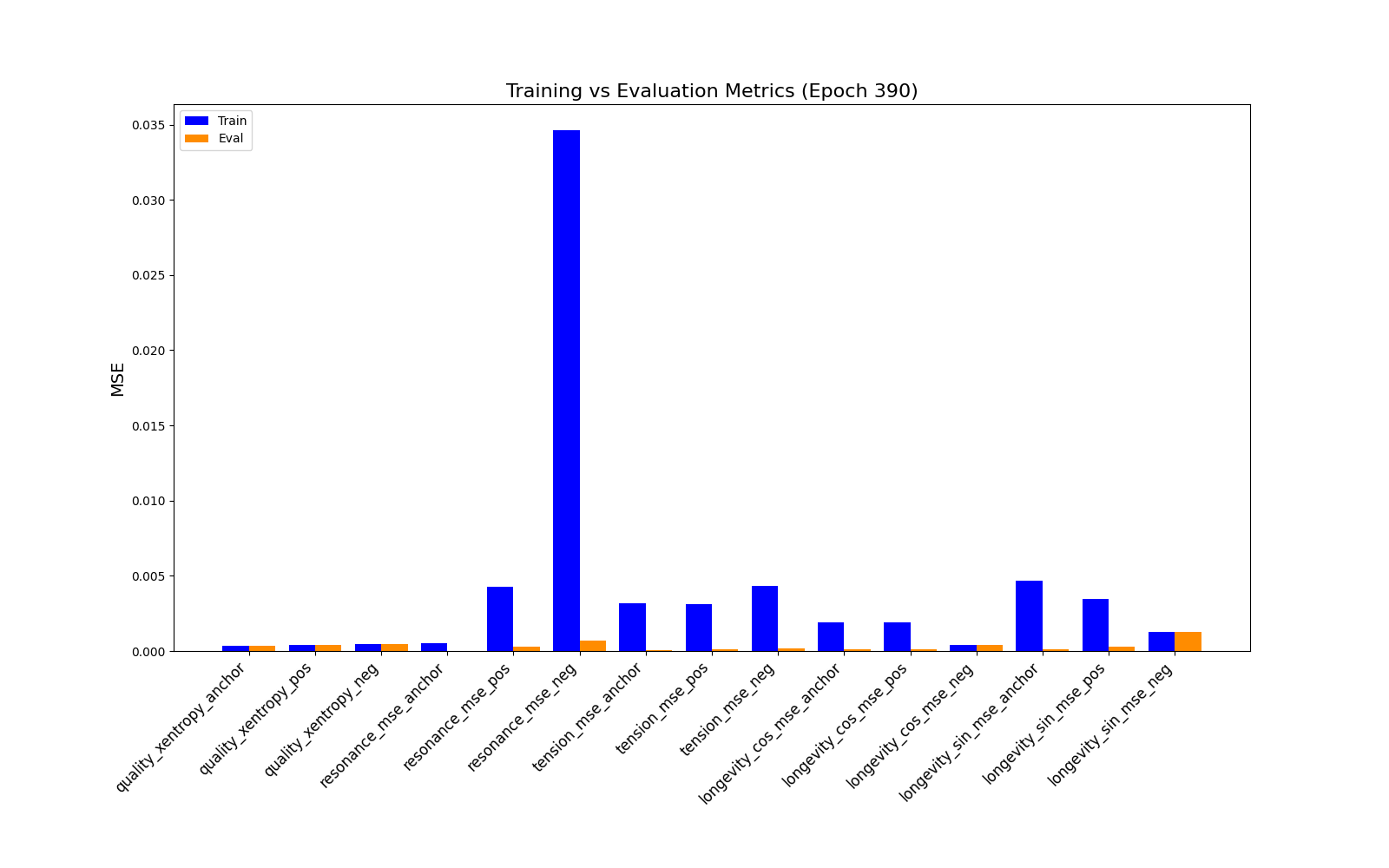
Reconstruction error results:

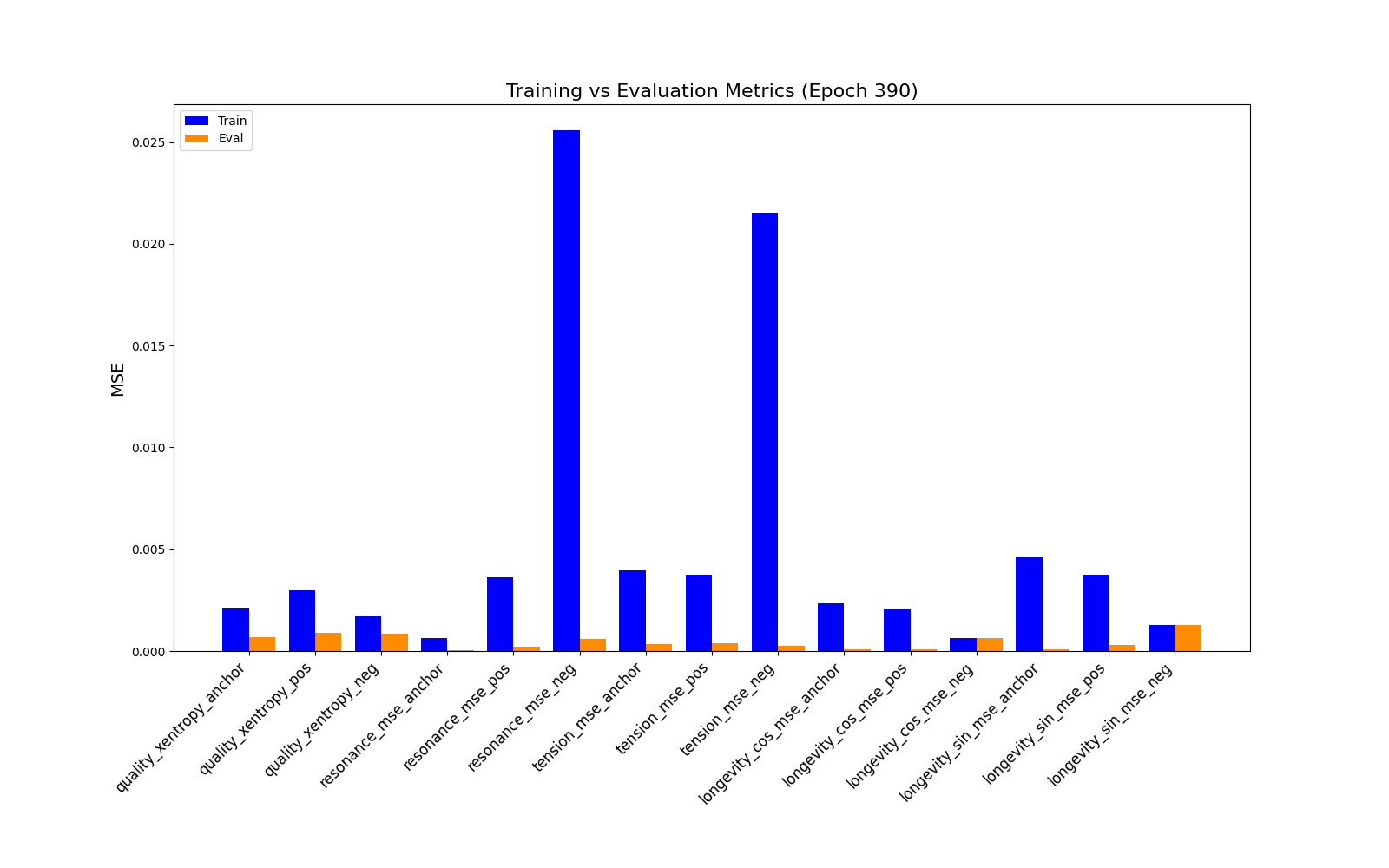
Since we achieve total separation, AUROC=1. Assuming contrastive 70% threshold, we get 100% F1, recall and precision. This indicates embeddings may be collapsing.

Hierarchical Clustering Results

We input the resulting embeddings of our test dataset from running inference with the trained encoder using the contrastive loss criterion and without layer normalization. We fit the AgglomerativeClustering method with a low ecludean distance threshold of 0.2.

We find the distances of the embeddings are not correctly separated. The clustering algorithm cannot semantically classify correctly classes when these are not provided as triplets.

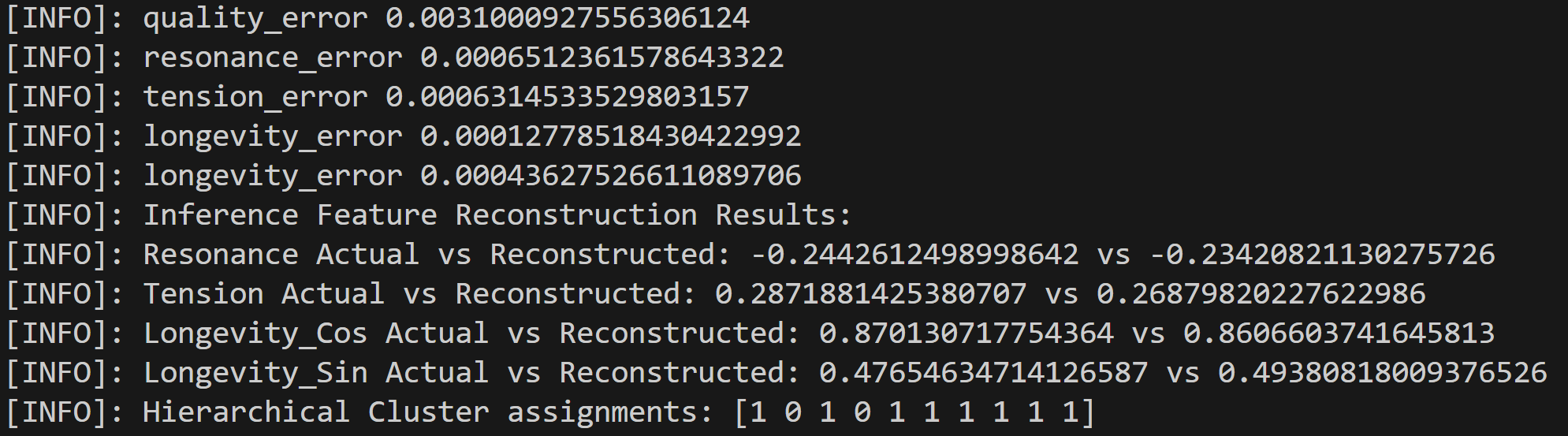
Hierarchical clustering results: [1 0 1 0 1 1 1 1 1 1]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1]

Inference Reconstruction error performs well:

Conclusions:

• Margin=1 loss reaches zero immediately. Margin=2 takes a few more epochs but the clustering test dataset results are the same.

Despite we achieve training and evaluation feature embeddings similarity separation in the embedding space, the representations similarities for the training, evaluation and test datasets indicate the model is pushing dissimilar pairs to the margin boundary and those similar to the other extreme. Pretty much and as mentioned in the literature, embeddings seem to collapse into a small sub-space so the clustering result is binary instead of the model learning the subtleties of the data.

Hierarchical Cluster results at Epoch 10: [0 3 0 3 0 1 0 2 1 0]
Hierarchical Cluster results at Epoch 50: [0 1 0 1 0 0 0 0 0 0]
Hierarchical Cluster results at Epoch 100: [0 1 0 1 0 0 0 0 0 0]
Hierarchical Cluster results at Epoch 400: [1 0 1 0 1 1 1 1 1 1]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1] (clusters here are 0 and 1 but their order makes no difference).

The above mentioned paper offers multiple explanations including as training proceeds, (S)GD forgets the learned subclass features and collapses class representations. In our scenario semantic representations fail but the reconstruction error is relative low.

Furthermore, we consider that during training the model focuses execessively on the easier triplets so that when these are a majority and their loss near zero, the model stops learning and fails to generalize. Intuition follows that early training focus on harder-negatives can help the model bring positives and negatives more optimally apart.

If the algorithm is trained with excessive "easy" triplets, the model may gravitate to a suboptimal output that does not generalize well., Deval Shah

We note the hierarchical clustering results with with dataloader shuffle enabled results in similar feature reconstruction errors but significantly worse clustering results:

Hierarchical clustering results: [0 1 0 1 0 0 0 0 0 0]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1]

Experiment 1.B - A Quick Detour: Contrastive Loss with Early Layer Normalization

The above mentioned results led us to believe the model overfits. We add batch normalization to the early layers for better generalization, the rest of the modelling assumptions remain.

We found the training is significantly slower and combined loss plateaus higher (0.05 vs 1.0); evaluation results follow training with several epochs lag and it results in worse separation and evaluation accuracy results. This is in line with with the findings outlined in The Danger of Batch Normalization in Deep Learning.

Training Loss:

Comparable successful separation results:

Embedding Representations Training Evolution visualized in a 2D Manifold: You can see the full training evolution here.

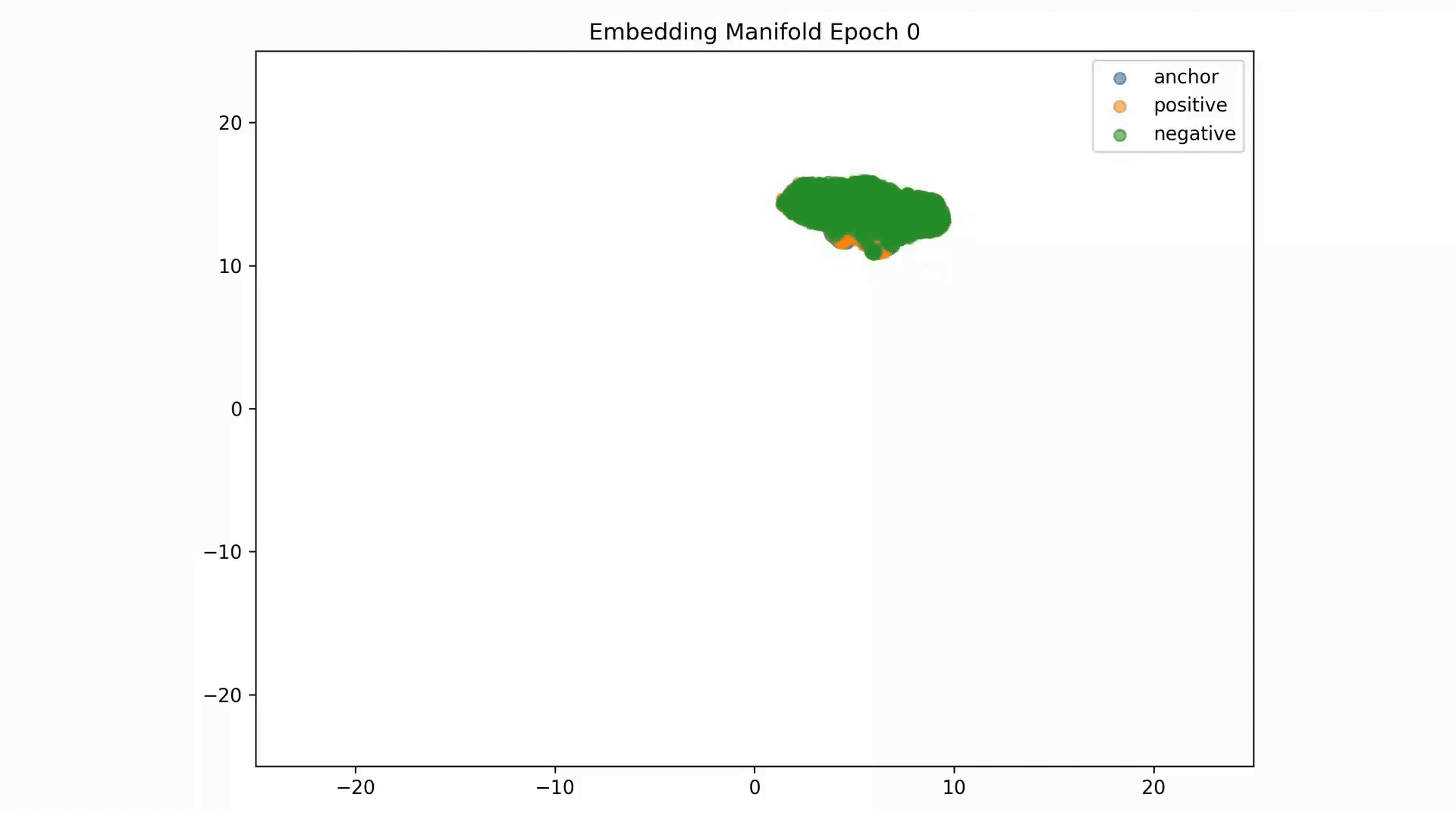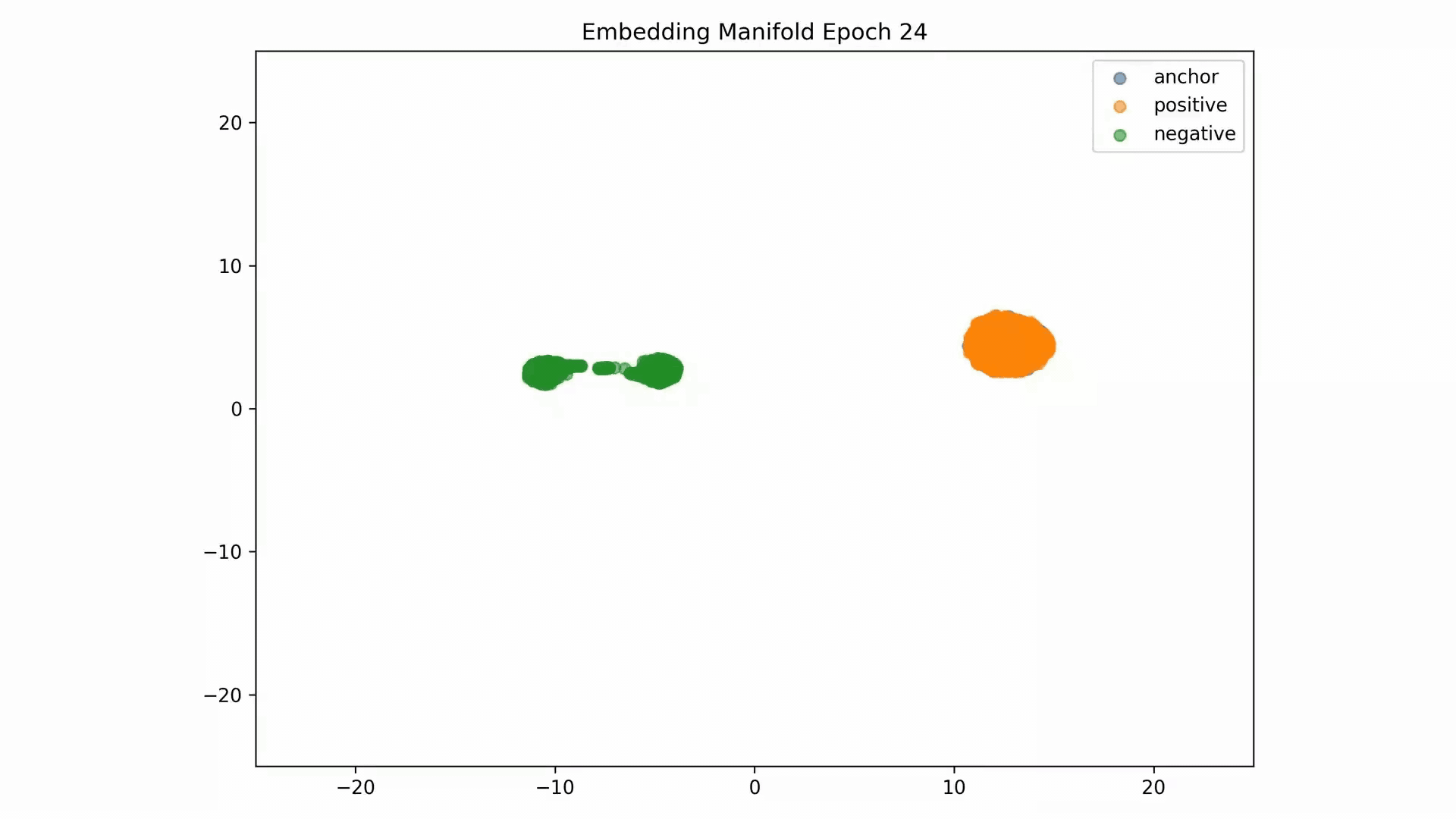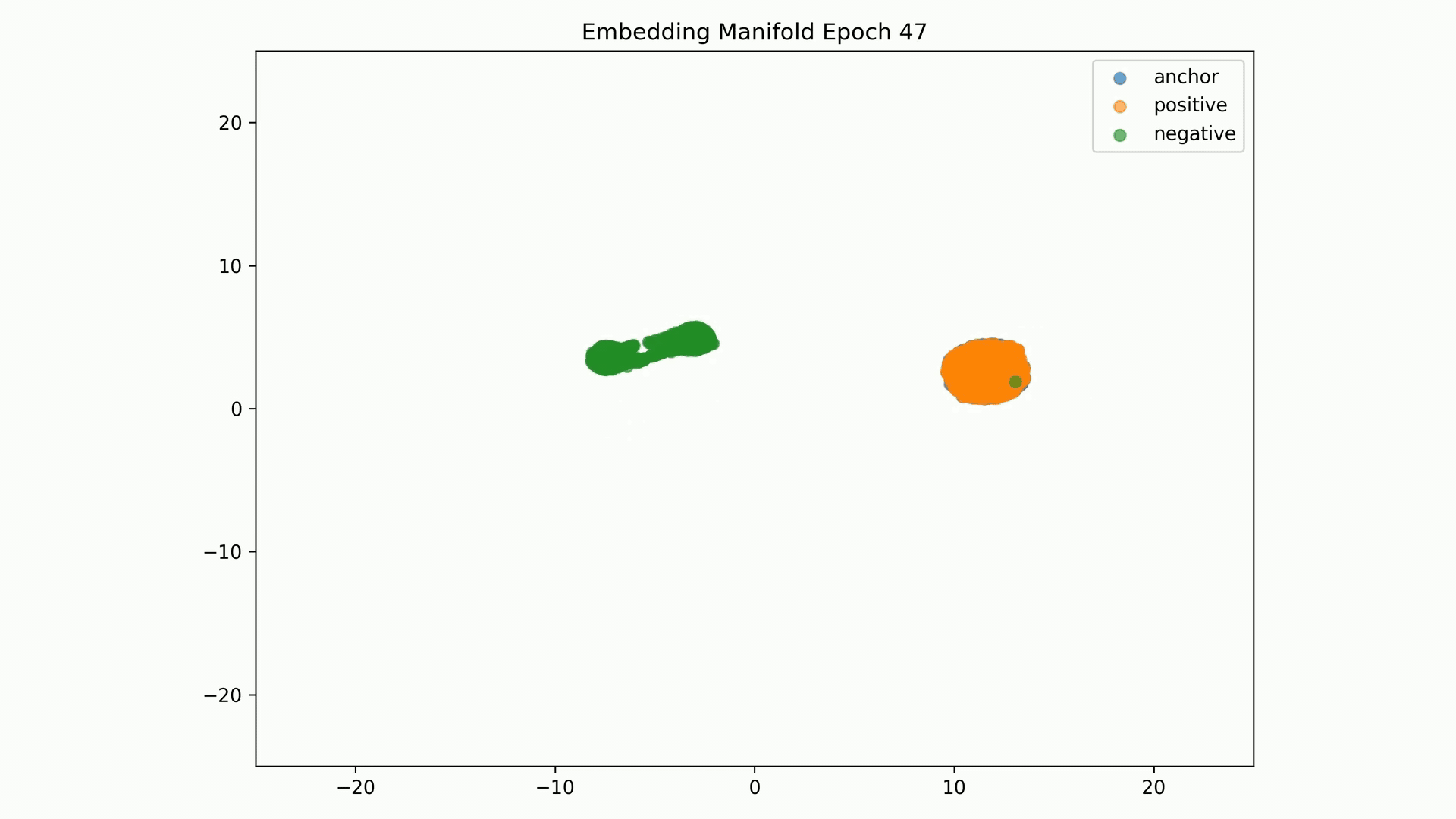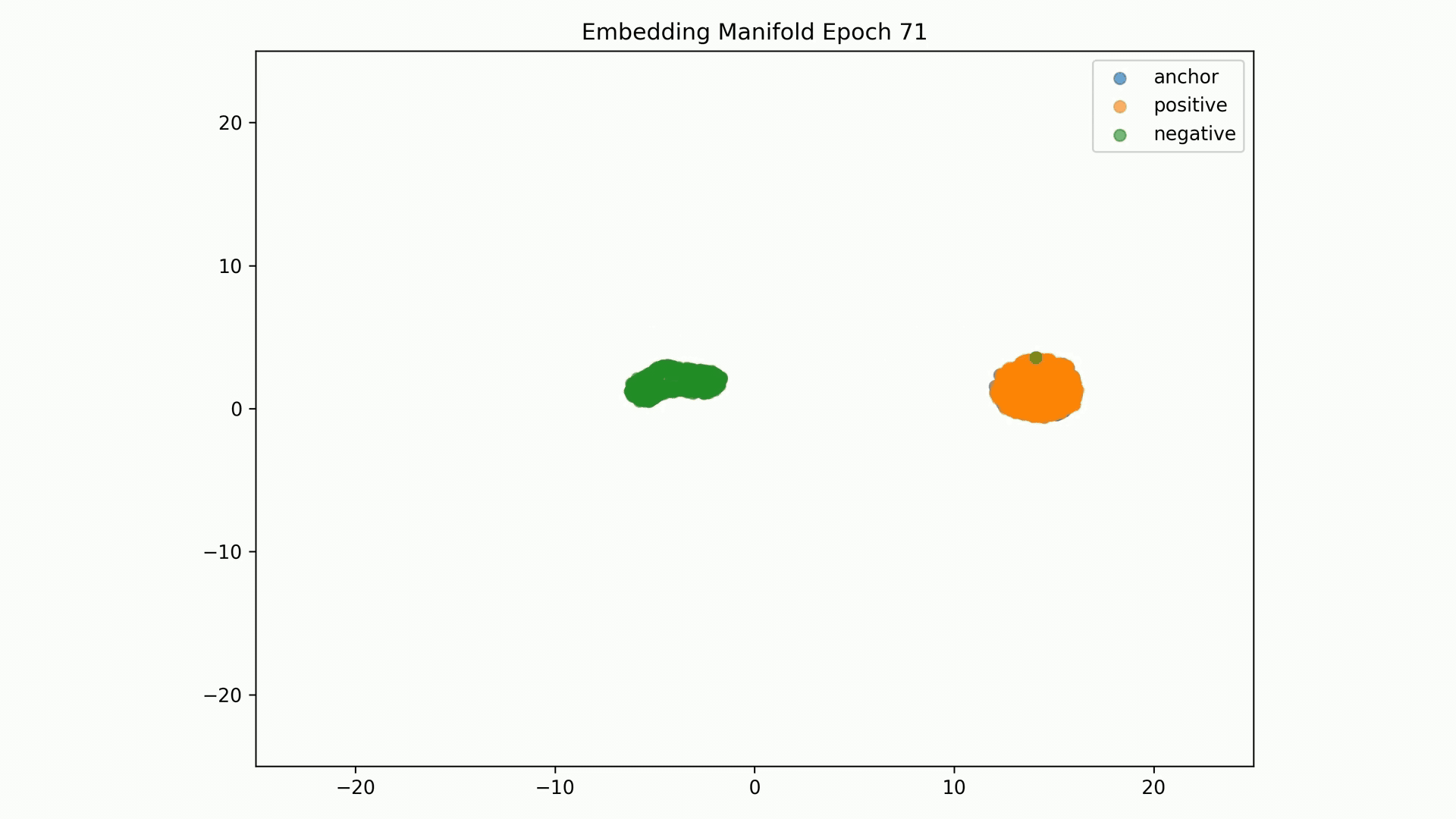
Worse Evaluation Reconstruction error metrics, particular for the tension feature:

Hierarchical Clustering Results: Contrastive Approach With Normalization

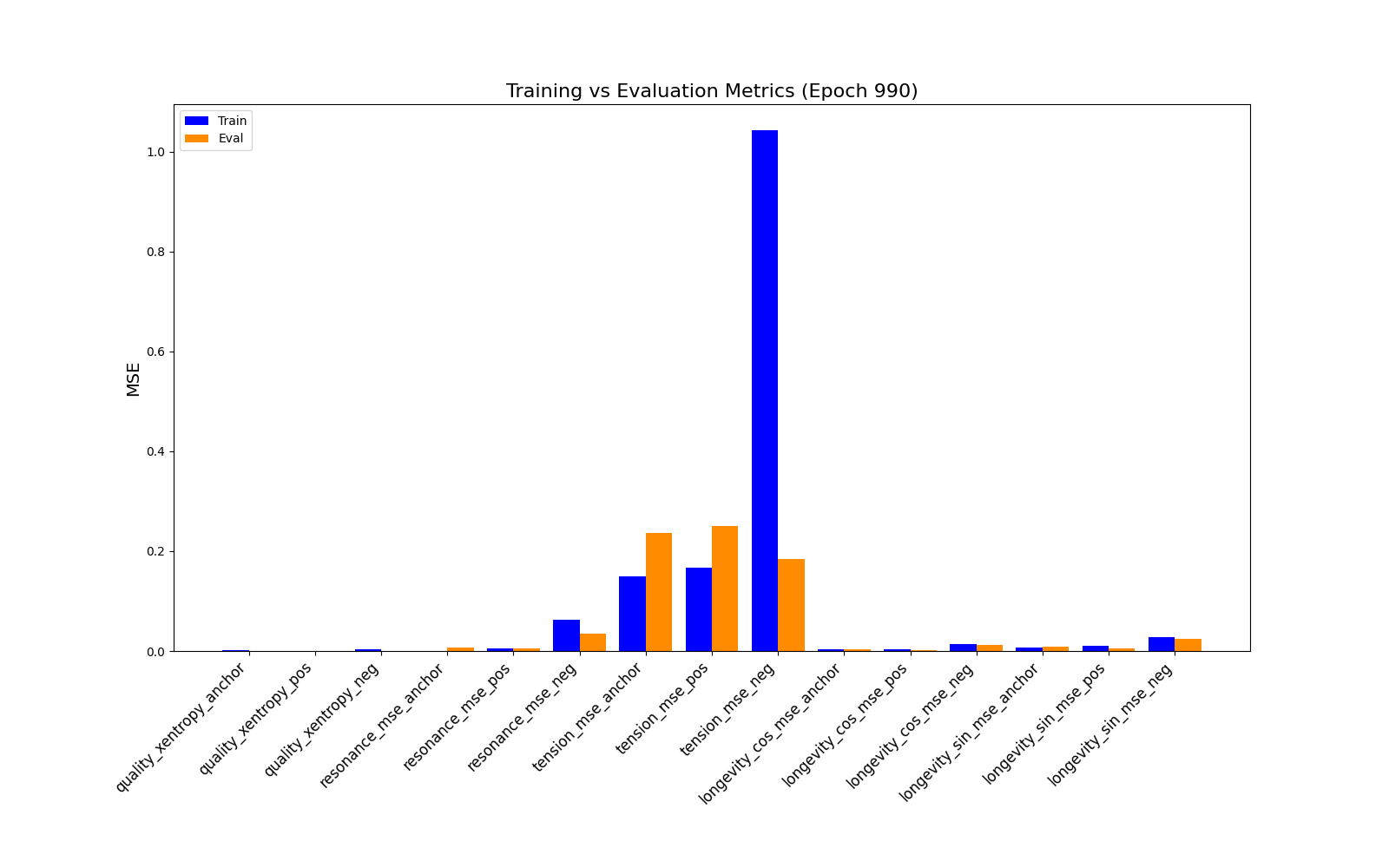
We obtain similar results to our prior experiement. Inference Reconstruction error performs well except for the tension feature:

Hierarchical clustering results: [1 0 1 0 1 1 1 1 1 1]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1]

Experiment 2: Triplet Margin Loss

We train the model with Pytorch's TripletMarginLoss loss criterion implementation.

Other modelling assumptions:

• we apply TripletMarginLoss criterion
• we enable the dataLoader shuffle
• we apply the remaining assumptions as outlined in our experiment outlined above where we applied Contrastive loss.

Training triplet marginig loss converges quickly.

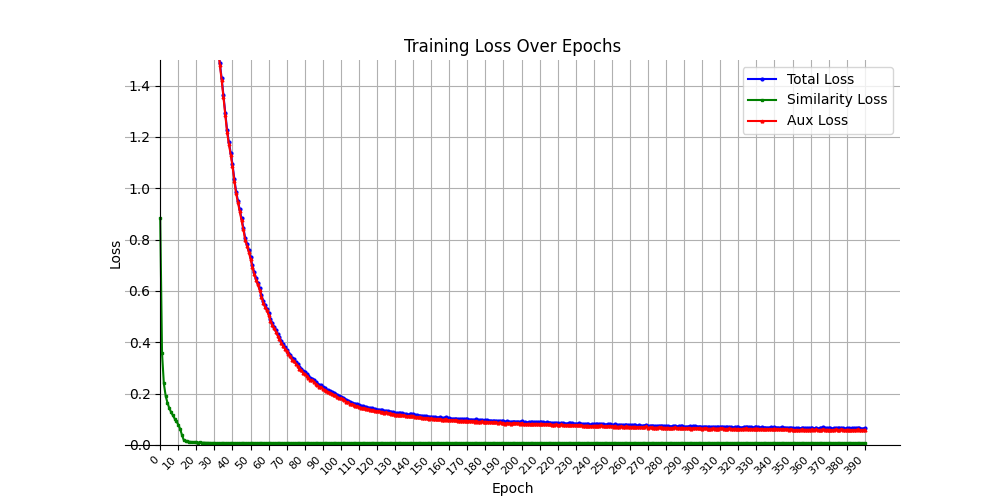
Anchor-positive distance separation from anchor-negative Evaluation are good results, but visualization of these embeddings on a 2D manifold show that these are not stable:

Embedding Representations Training Evolution visualized in a 2D Manifold: Shows the relative distances between entity embedding vectors and the clusters these form. You can see the full training evolution here.

Reconstruction error results:

It results in AUROC=1. Assuming contrastive 70% threshold, we get 100% F1, recall and precision. This indicates embeddings may be collapsing.

Hierarchical Clustering Results for the model trained with TripletMarginLoss Criterion

The clustering algorithm semantically classifies the classes correctly despite these are not provided as triplets.
Inference Reconstruction error performs well.

Hierarchical clustering results: [0 0 0 0 0 1 1 1 1 1]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1]

We note hierarchical clustering results with the dataloader shuffle disabled results in similar feature reconstruction results but worse clustering classifications:

Hierarchical clustering results: [0 1 0 1 0 0 0 0 0 0]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1]

Network Tested with Triplet Margin Loss criterion and Enhanced Test Dataset

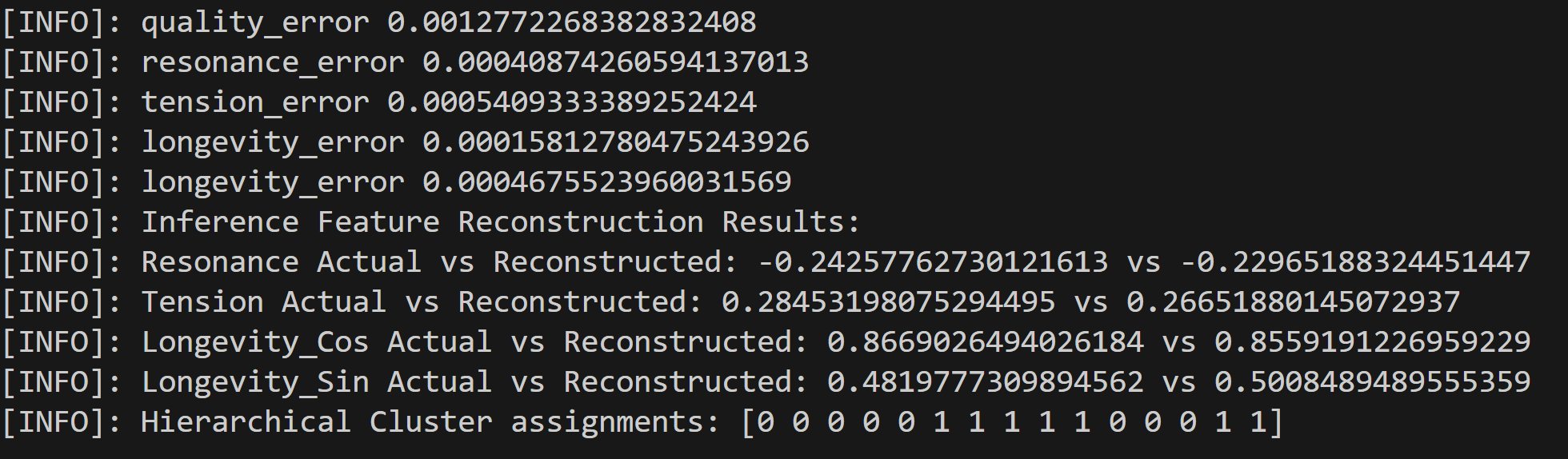
We run inference on the model and clustering algorithm using the test enhanced dataset.

Feature reconstrution error results are good.
We find the quality feature drives the cluster result since record 13 should be allocated to cluster zero and record 14 to 1:

Hierarchical cluster results: [0 0 0 0 0 1 1 1 1 1 0 0 0 1 0]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1 0 0 0 0 1]

This second enhanced dataset helps us conclude learned embedding representations are not fully meaninful and the model may be incorrectly overrepresenting certain features.

Experiment 3: Network Trained with Triplet Margin Loss criterion And Hard-Mined Triplet samples

We aim at focusing on the hardest negative samples.

We exclude 1% of the easier anchor-positives for each batch which are already effectively learned and contribute zero loss; and keep the hardest 5% of the anchor-negatives. A surviving batch sample meets both criteria.

valid_positives = dist_ap >= pos_threshold
valid_negatives = dist_an <= neg_threshold
valid_triplets = valid_positives & valid_negatives

Other modelling assumptions:

• we apply TripletMarginLoss criterion
• we enable the dataLoader shuffle
• we apply the remaining assumptions as outlined in our experiment outlined above where we applied Contrastive loss

Surviving Samples during Training and Training Loss Evolution

Anchor-positive separation from anchor-negative results

Embedding Representations Training Evolution visualized in a 2D Manifold: You can see the full training evolution here

Reconstruction error results:

Since we achieve total separation, AUROC=1. Assuming contrastive 70% threshold, we get 100% F1, recall and precision. This indicates embeddings may be collapsing.

Hierarchical Clustering Results

The inference feature reconstruction error results are good and the clustering algorithm correctly classifies the records.

Hierarchical clustering results: [0 0 0 0 0 1 1 1 1 1]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1]

We note hierarchical clustering results with the dataloader shuffle disabled results in similar feature reconstruction results but worse clustering classifications:

Hierarchical clustering results: [0 1 0 1 0 0 0 0 0 0]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1]

Hierarchical Clustering Results using the Enhanced Test Dataset

We test the testing enhanced dataset and the model trained with the triplet margin loss criterion and hard-negative mined samples.

Feature Reconstrution error results are good.
We find the quality feature can drive the cluster result since record 13 should be allocated to cluster zero. The cluster result for record 14 also points to this possible behaviour.

Hierarchical cluster results: [0 0 0 0 0 1 1 1 1 1 0 0 0 1 0]
Ground truth clustering results: [0 0 0 0 0 1 1 1 1 1 0 0 0 0 1]

Undocumented Tests

We performed additional tests that we have not documented in this blog for readibility. We didn't research these in depth but tested its impact via straight implementation. None of these improved semantic representations.

• Remove model output embeddings normalization before the loss calculation to capture magnitude
• Margin: 0.25 - 2 with dataloader shuffle disabled
• Train the model using different proportions of the reconstruction and semantic loss criterion. The loss schedules were stagged, front and backloaded to test the impact of semantic representation loss at different training stages. Example:

alpha = min(epoch / num_epochs, 0.5)
loss = (alpha * batch_triplet_loss if alpha>0.25 else 0) + ((1-alpha) * batch_aux_loss if alpha>0.25 else batch_aux_loss)

• Early stopping results once the triplet loss reached ~zero
• Batch size 128, 246, 512, 1024 with dataloader shuffle disabled
• Dataloader shuffle enabled and disabled. Here we only show the better results of the two.
• Hard-mined triplet sampling scenario from both anchor-positive and anchor-negative distance distribution batches and select those pairs that are statistically meaningful. The approach was inspired on this paper
• CircleLoss criterion implementation in the current network architecture.

Conclusion

We tested training models for learned feature representations with a feed-forward neural network. The objective was for these embeddings to serve as inputs to a machine learning algorithm that would solve entity resolution. Our hypothesis assumed that by generating embeddings of each entity in the representation space and that were sufficiently far apart based on similarity, this would help the ML algorithm create entity clusters.

A model trained with the contrastive criterion does not generate meaningful learned entity representations which we measure by similarity. The extreme similarity results exhibited at inferrence by record-pairs leads us to believe that embeddings collapse into a small sub-space so the clustering result is binary instead of learning the subtleties of the data; by collapsing, the resulting embeddings are not very informative of the input. We see this result at inference on a distance matrix of all records. Thus the clustering algorithm cannot semantically classify classes correctly at inference when these are not provided as triplets.

The triplet margin loss and its hard-mining variation approach perform well on reconstruction tasks but semantic representations can be biased for some features whereby the model places too much weight to a feature. Thus the clustering algorithm can fail to classify records correctly. Further research may yield interesting results by addressing this inbalance perhaps via attention mechanism heads for the entity features or by calibrating each features' weight on the combined concatinated embedding.

The model trained with the triplet margin loss criterion performs above the rest, and hard-mining doesn't stand above its vanilla implementation with these testing datasets.

Given the methods and architecture changes considered, we deem the results inconclusive. A rethink of the network architecture would help to achieve meaningful semantic representations.

We tested the network at inference with the triplet margin loss and hard-mining triplet margin loss criterions and it successfully clustered 10 records in 2 groups. However the model seems to place too much weight on certain features leading to incorrect edge classifications for the testing enhanced dataset.

The network can be tweaked to address these biases. However we are more inclined to attribute the missclassification to the model's inability to learn representations semantically with its current architecture for a tabular dataset.

Feed-forward neural networks are generally not sensitive to rotation or are rotation-invariant and learn based on spatial structure and geometry in the feature space which occurs through rotational transformations. However tabular data is heterogenous by nature, its features are often independent, sparse and lack spatial correlation; we observe that when rotating the network's weight matrices its impact to the data (e.g. mixing features such as quality and tension in a concatinated layer) destroys the semantic meaning of features in the representation space.

Factoring these findings into a re-worked network architecture may get a network closer to par with machine learning models like tree-based models that treat features independently.

Tech Stack

Language: Python
Key Libraries: Pytorch, Sklearn, Torchmetrics, Matplotlib
Tested on Windows 11 system, 64GB RAM, GPU NVIDIA GeForce RTX 5080 16GB, NVIDIA GeForce RTX 3090 32GB, CPU 12th Gen Intel i9-12900K, 3400Mhz, 16 cores.

Project Files

Model trained with Contrastive Loss criterion files
Model trained with Triplet Margin Loss criterion files
Model trained with Triplet Margin Loss criterion and hard-negative mining sampling triplets - files

References

Triplet Loss: Intro, Implementation, Use Cases
Triplet Loss - Advanced Intro
Embedding Expansion: Augmentation in Embedding Space for Deep Metric Learning
Outlier-suppressed triplet loss with adaptive class-aware margins for facial expression recognition
Adaptive Real-Time Multi-Loss Function Optimization Using Dynamic Memory Fusion Framework: A Case Study on Breast Cancer Segmentation
Classic contrastive loss paper, Raia Hadsell, Sumit Chopra, Yann LeCun
Understanding the Behaviour of Contrastive Loss
Triplet training considerations
The Danger of Batch Normalization in Deep Learning, by Charles Gaillard and Rémy Brossard
FaceNet: A Unified Embedding for Face Recognition and Clustering
Which Features are Learnt by Contrastive Learning?
On the Role of Simplicity Bias in Class Collapse and Feature Suppression
The downside of rotation invariance in neural net training
Why Tree-Based Models Beat Deep Learning on Tabular Data
Why do tree-based models still outperform deep learning on typical tabular data?

© 2025 Sergio Solorzano Gimenez. This work is licensed under Creative Commons Attribution 4.0 International License (CC BY 4.0).

This is a preprint version. Cite as: Solorzano Gimenez, S. (2025). Entity Resolution: Learned Representations of Tabular Data with a Classic Neural Network. [Preprint]. ReadyTensor. The content has not undergone peer review and is subject to change. Zenodo 10.5281/zenodo.15611742

Keywords: entity resolution, deduplication, linkage, neural networks, deep learning, triplet loss, learned embeddings, machine learning, hierarchical clustering, tabular data