In the rapidly evolving field of survival analysis, the integration of deep learning has brought forward numerous innovations that have significantly improved the accuracy and scalability of predictive models. One such advancement is encapsulated in the concept of Survival Kernets—a novel approach that combines the strengths of kernel methods with deep learning to address the challenges of large-scale, high-stakes applications like healthcare. In this detailed exploration, This method delve into the intricacies of Survival Kernets, as introduced by George H. Chen in his paper titled "Survival Kernets: Scalable and Interpretable Deep Kernel Survival Analysis with an Accuracy Guarantee."

Introduction to Survival Analysis

Survival analysis models the time until an event of interest occurs, such as death, disease relapse, or equipment failure. Traditionally, this field has grappled with the complexity of censored data, where the event of interest has not yet occurred for some subjects during the study period. This leads to partial information that complicates the modeling process.

As datasets grow larger and applications become more critical, there is an increasing demand for models that are not only accurate but also scalable and interpretable. This is where the Survival Kernet model steps in, offering a promising solution that scales efficiently with large datasets while providing a level of interpretability that is crucial for decision-making in sensitive areas like healthcare.

What Are Survival Kernets?

Survival Kernets extend the deep kernel method by introducing a novel training set compression scheme known as kernel netting, which was originally developed for classification and regression. This technique allows the model to be both scalable during training and efficient at test time, addressing the significant computational demands of large datasets.

Key Features of Survival Kernets:

Survival Kernet is not just any patient specific survival prediction method, it has some unique features that make it stand out from other models. Here are some of the key features of Survival Kernets:

1. Scalability: Uses a compression technique to construct a test-time predictor that efficiently handles large datasets.
2. Interpretability: Represents each data point by a weighted combination of clusters, which can be visualized and analyzed to understand the model’s predictions.
3. Accuracy Guarantee: For a special case of the model, it offers a theoretical accuracy guarantee on the predicted survival distributions.

Mathematical Foundations of Survival Analysis

The model framework for Survival analysis involves training data points represented as follows:

• :
  • denotes the feature vector of the i-th training point.
  • is the observed nonnegative time duration, with .
  • is the event indicator, where :
    • : Event (e.g., death) has occurred.
    • : Data is censored (event has not occurred by the end of the study).

Data Generation Process

Each data point is assumed to be generated independently and identically distributed (i.i.d.) via the following process:

1. Feature Vector Sampling:
   • Sample feature vector .
2. Survival Time Sampling:
   • Sample nonnegative survival time .
3. Censoring Time Sampling:
   • Sample nonnegative censoring time .
4. Event and Censoring Logic:
   • If : Set and (event occurred).
   • Otherwise: Set and (data is censored).

The distributions , , and are typically unknown to the learning method.

Conditional Survival Function

The primary goal is to estimate the conditional survival function for a test feature vector , defined as:

where is the cumulative distribution function (CDF) of the survival time given the feature vector .

Hazard Function

The hazard function , which describes the instantaneous rate of death at time , given survival until time , is defined as:

Here, is the probability density function (PDF) of the survival time, and is the survival function. Estimating thus provides an estimate for :

Conditional Survival Function

The primary goal is to estimate the conditional survival function for a test feature vector , defined as:

where is the cumulative distribution function (CDF) of the survival time given the feature vector .

Hazard Function

The hazard function , which describes the instantaneous rate of death at time , given survival until time , is defined as:

Here, is the probability density function (PDF) of the survival time, and is the survival function. Estimating thus provides an estimate for :

Kernel Methods in Survival Analysis

Kernel estimators play a critical role in the context of survival analysis by enabling the estimation of hazard functions using a kernel function that quantifies similarity between feature vectors.

Kernel Function

The kernel function measures the similarity between any two feature vectors, where a higher value indicates greater similarity. The specifics of how this function can be learned within a neural network framework will be discussed later. Initially, assume this function is pre-specified.

Hazard Function Estimator

The hazard function estimator leverages the kernel function to provide a robust statistical measure of risk or hazard at different time points.

Hazard Function Estimation Process:

1. Define Time Points: Let denote the unique times of death observed in the training data, with .
2. Kernel-Based Estimator: The hazard function for time indices and for any feature vector is estimated as: Here, is the indicator function, active (1) when its argument is true. This estimator calculates the probability of dying at time given survival beyond .

Interpretation:

• When for all , the numerator counts the deaths at , and the denominator counts those who survived past .
• If both the numerator and denominator are zero, This method define the result as zero (convention for ).

Survival Function Estimator

The estimated hazard function can be utilized to estimate the conditional survival function through the product of empirical survival probabilities from time 0 up to :

This estimator is termed the conditional Kaplan-Meier estimator, which aligns with the methodology proposed by Beran (1981) and has known finite-sample error bounds as per Chen (2019).

Classical Kaplan-Meier Estimator

In a specific scenario where the kernel function equals 1 between all pairs of feature vectors, This method revert to the classical Kaplan-Meier estimator:

This formulation does not depend on feature vectors and offers a population-level estimate of the survival curve.

Deep Kernel Survival Analysis

The foundation of Survival Kernets lies in deep kernel survival analysis. This method employs a kernel function to measure the similarity between data points, which is crucial for estimating individual survival distributions. The kernel function is learned through a deep learning framework, which allows the model to capture complex, nonlinear relationships in the data.

Learning the Kernel Function

The kernel function is central to the model's ability to measure the similarity between any two data points, which is critical for accurately estimating the survival and hazard functions.

Kernel Function Definition

• **Kernel Function **: This function maps a pair of inputs from the embedding space into the non-negative real numbers , indicating the degree of similarity between them.
• **Embedding Function **: A neural network that transforms the raw feature vector into an embedding vector , where and is a subset of .
• **Distance Function **: This function computes the Euclidean distance between two embedded points, expressed as .

Example Kernel Function

A commonly used kernel function in this framework is the Gaussian kernel:

where is a variance hyperparameter that the user specifies.

Training Process

Base Neural Network Architecture

Users can select an appropriate neural network architecture based on the data characteristics:

• For image data: Convolutional Neural Network (CNN)
• For time series data: Recurrent Neural Network (RNN)

Loss Functions

• Negative Log-Likelihood Loss (LNLL): This is used for training the base neural net and is defined as follows:

• Binary Cross-Entropy Loss (LBCE):

  where is the sorted time index corresponding to .

DeepHit Ranking Loss Integration

To further enhance model performance, the DeepHit ranking loss can be integrated, focusing on the differences in survival predictions among data points:

Implementation Considerations

Handling Overfitting

To prevent overfitting:

• Use a leave-one-out approach for the hazard estimates during training.
• Regularize by discretizing time into equal steps, which helps smooth the estimated functions.

Kernel Function with Infinite Support

Using a Gaussian kernel or any other infinite-support kernel function is recommended to avoid issues with vanishing gradients that can occur if the kernel function has finite support and is improperly initialized.

Practical Applications and Improvements

By adopting deep kernel survival analysis, researchers and practitioners can build more robust, interpretable, and accurate survival models capable of handling complex datasets typical in fields like healthcare and engineering.

Survival Kernet

The challenge of making predictions in large training datasets involves computing the similarity between a test feature vector and every training feature vector. This process is computationally expensive and not feasible at scale. To address this issue, This method implement a technique known as kernel netting, adapted from Kpotufe and Verma (2017), into our deep kernel survival analysis framework to create what This method call a "survival kernet."

Kernel Netting and ε-nets

Kernel netting helps to construct a compressed version of the training data for use at test time, leveraging the concept of ε-nets. This method significantly reduces the computational overhead by simplifying the data structure that needs to be analyzed during the prediction phase.

Sample Splitting and Theoretical Guarantees

For ensuring robustness in predictions, This method employ a sample splitting technique where the base neural network is trained on pre-training data that is independent of the main training data. This approach helps in providing a theoretical guarantee on the prediction error at test time.

Training Survival Kernets

Here's a step-by-step breakdown of the training procedure for a survival kernet:

1. Pre-Training Data Setup:

   • Utilize pre-training data to train the base neural net , optimizing the deep kernel survival analysis loss with minibatch gradient descent.
   • The neural net learned from this data is denoted as .

2. Embedding and Nearest Neighbor Setup:

   • Compute embedding vectors for the actual training data using and set up a Euclidean-distance-based nearest neighbor data structure.

3. Constructing ε-nets:

   • Use the nearest neighbor structure to create a subsample that acts as an ε-net, efficiently summarizing the training data.

4. Cluster Assignment and Summary Functions:

   • Assign each training embedding vector to its closest exemplar in .
   • Calculate summary functions for these clusters to use in prediction.

Making Predictions

To predict for a new test feature vector :

1. Compute Embedding:

   • Determine the embedding vector .

2. Hazard Estimation:

   • Formulate the hazard estimate using the clusters and their summary functions, adjusting for the proximity within the threshold distance .

3. Conditional Survival Function:

   • Estimate the survival function based on the hazard estimates across all relevant clusters.

Interpretability and Visualization

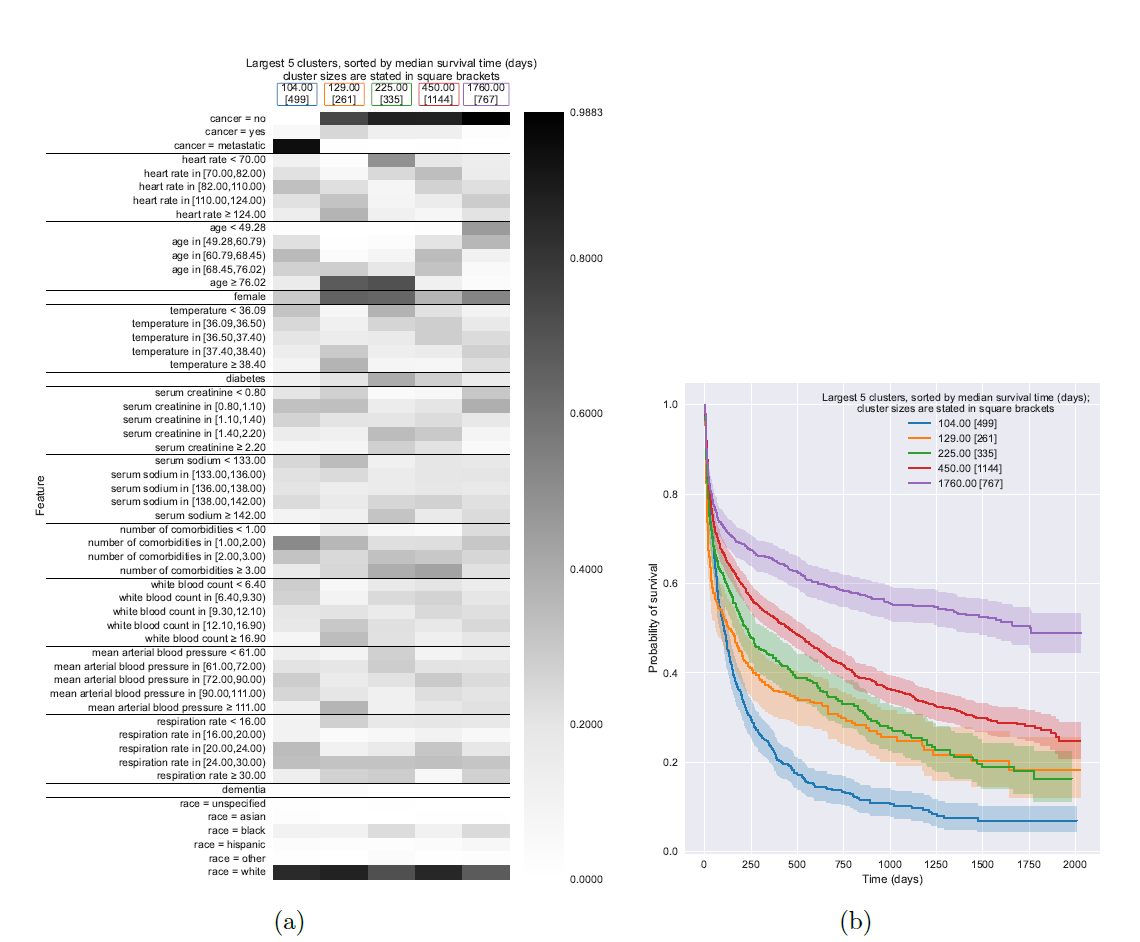
Model interpretability is crucial, especially in high-stakes fields like healthcare, where understanding the rationale behind predictions can significantly impact decisions. The Survival Kernets model enhances interpretability through visual tools such as heatmap visualizations of clusters. Each cluster in the heatmap corresponds to a group of training points (exemplars) that share similar features. These heatmaps allow quick visual assessments of how different clusters vary in terms of specific feature values, offering insights into the data's underlying patterns.

For instance, in a study involving hospitalized patients, heatmaps could show that one cluster mainly consists of older patients with metastatic cancer, while another consists predominantly of younger, cancer-free individuals. This visualization helps in quickly identifying which features are common in patients with similar prognoses and treatment outcomes.

Furthermore, the model uses the Kaplan-Meier survival curves for each cluster to provide a more detailed understanding of survival probabilities over time. These curves, plotted with confidence intervals, not only illustrate the survival estimates for each cluster but also allow comparisons across different patient groups. Such comparisons can reveal which groups are more vulnerable or have better survival prospects, guiding more tailored and effective interventions.

By integrating these interpretative tools, Survival Kernets make it easier for researchers and practitioners to see the connections between features and survival outcomes, facilitating a deeper understanding of the model's predictions. This approach not only aids in model validation and improvement but also enhances the collaborative process with domain experts, potentially leading to significant advancements in personalized medicine.

Experimental Results and Comparative Analysis

Understanding the Empirical Performance of Survival Kernets: An In-Depth Experimental Analysis

Introduction to Survival Kernets Experiments

In our exploration of survival kernets, a refined method for survival analysis, This method systematically evaluate their performance focusing on prediction accuracy, computational efficiency, and visual interpretability. The experiments outlined here illustrate the practical application and effectiveness of survival kernets across various datasets, comparing them against established baselines within the field.

Datasets Employed

This method utilized four well-known survival analysis datasets, each with unique characteristics that challenge the models in different ways:

1. Rotterdam/GBSG: Combines data from the Rotterdam tumor bank and the German Breast Cancer Study Group, focusing on breast cancer patients.
2. SUPPORT: Involves data from hospitalized patients, aiding in understanding prognoses and treatment outcomes.
3. UNOS: Contains data from heart transplant patients, sourced from the United Network for Organ Sharing.
4. KKBOX: Focuses on customer churn within the KKBOX streaming service.

The datasets vary in size, features, and censoring rates, providing a comprehensive test bed for our survival models.

Baseline Models

To benchmark survival kernets, This method compare them against several baseline models:

• Elastic-net regularized Cox model
• XGBoost
• DeepSurv
• DeepHit
• Deep Cox Mixtures (DCM)
• DKSA (Deep Kernel Survival Analysis)

These models represent a mix of traditional and neural network-based approaches, providing a diverse set of competitors.

Variants of Survival Kernets

This method experimented with different configurations of survival kernets to optimize performance:

• With and without summary fine-tuning
• With and without the TUNA warm-start procedure

These variations help in understanding the impact of initialization and fine-tuning on the model's effectiveness.

Results

Let's incorporate detailed results in tables to provide a comprehensive overview of the experimental findings for the survival kernets across the four datasets. Here are the summarized tables:

Table: Test Set Ctd Indices (Mean ± Standard Deviation)

* Indicates only one experimental run due to computational constraints.

Table: Total Training Time (Mean ± Standard Deviation)

* Indicates only one experimental run due to computational constraints.

Conclusion of Survival Kernets Experiments

The comprehensive evaluation of survival kernets across multiple datasets and against various established models has highlighted their superior performance in both prediction accuracy and computational efficiency. These experiments underline the potential of survival kernets to handle large-scale and complex datasets effectively, a significant advancement over traditional models often limited by the scale and complexity of data.

Survival kernets excel in blending the robustness of kernel methods with the flexibility of deep learning, providing not only high accuracy but also improved interpretability through innovative visualization techniques such as cluster heatmaps and Kaplan-Meier curves. These features make survival kernets particularly valuable in fields where understanding the model's decision-making process is crucial, such as in healthcare and customer retention strategies.

The introduction of methods like the TUNA warm-start procedure and summary fine-tuning further enhances the model’s efficiency, making survival kernets a practical choice for real-world applications where speed and reliability are critical. Moreover, the models' ability to maintain high performance across diverse datasets emphasizes their robustness and adaptability.

In conclusion, survival kernets mark a significant step forward in the domain of survival analysis. They offer a scalable, accurate, and interpretable option, proving to be a powerful tool for analysts and practitioners across various industries. This makes them a compelling alternative to traditional survival analysis techniques, setting a new benchmark in the field.

References

1. Foekens, J.A., et al. (2000). "Rotterdam tumor bank dataset."
2. Schumacher, M., et al. (1994). "German Breast Cancer Study Group dataset."
3. Knaus, W.A., et al. (1995). "Study to Understand Prognoses, Preferences, Outcomes, and Risks of Treatment (SUPPORT)."
4. Katzman, J.L., et al. (2018). "DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network."
5. Lee, C., et al. (2018). "DeepHit: A Deep Learning Approach to Survival Analysis with Competing Risks."
6. Nagpal, C., et al. (2021). "Deep Cox Mixtures for Survival Regression."
7. Chen, T., Guestrin, C. (2016). "XGBoost: A Scalable Tree Boosting System."
8. Kvamme, H., et al. (2019). "Time-to-event prediction with neural networks and Cox regression."
9. Malkov, Y., Yashunin, D. (2020). "Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs."
10. Antolini, L., et al. (2005). "Time-dependent concordance index for survival prediction models."
11. Kvamme, H., Borgan, Ø. (2021). "Continuous density interpolation strategies for survival analysis models."
12. Chen, G.H. (2020). "Survival Kernets: Scalable and Interpretable Deep Kernel Survival Analysis with an Accuracy Guarantee."