This publication explores Long Short-Term Memory (LSTM) networks, a specialized form of recurrent neural networks (RNNs) that excel at learning and predicting patterns in sequential data. We discuss the architecture, applications, and recent advancements in LSTM technology, with a particular focus on time series prediction tasks. The accompanying GitHub repository (https://github.com/pulinduvidmal/lstm-predictions) provides implementation examples and practical applications of the concepts discussed in this publication.
Sequential data is ubiquitous across domains—from financial markets and weather patterns to natural language and biological signals. The ability to model and predict such data is crucial for numerous applications. Traditional machine learning methods often struggle with sequential data due to their inability to capture long-range dependencies and temporal patterns effectively.
Long Short-Term Memory (LSTM) networks, introduced by Hochreiter and Schmidhuber in 1997, represent a breakthrough in handling sequential data. As a specialized form of recurrent neural networks, LSTMs address the vanishing gradient problem that plagues standard RNNs, enabling the learning of long-term dependencies in data.
This publication aims to provide a comprehensive understanding of LSTM networks, from their fundamental architecture to modern applications and research directions. We explore how LSTMs have evolved over time and examine their role in the current deep learning landscape.
Recurrent Neural Networks are designed to process sequential data by maintaining an internal state that can capture information from previous time steps. However, standard RNNs suffer from the vanishing gradient problem during backpropagation through time, making it difficult to learn long-term dependencies.
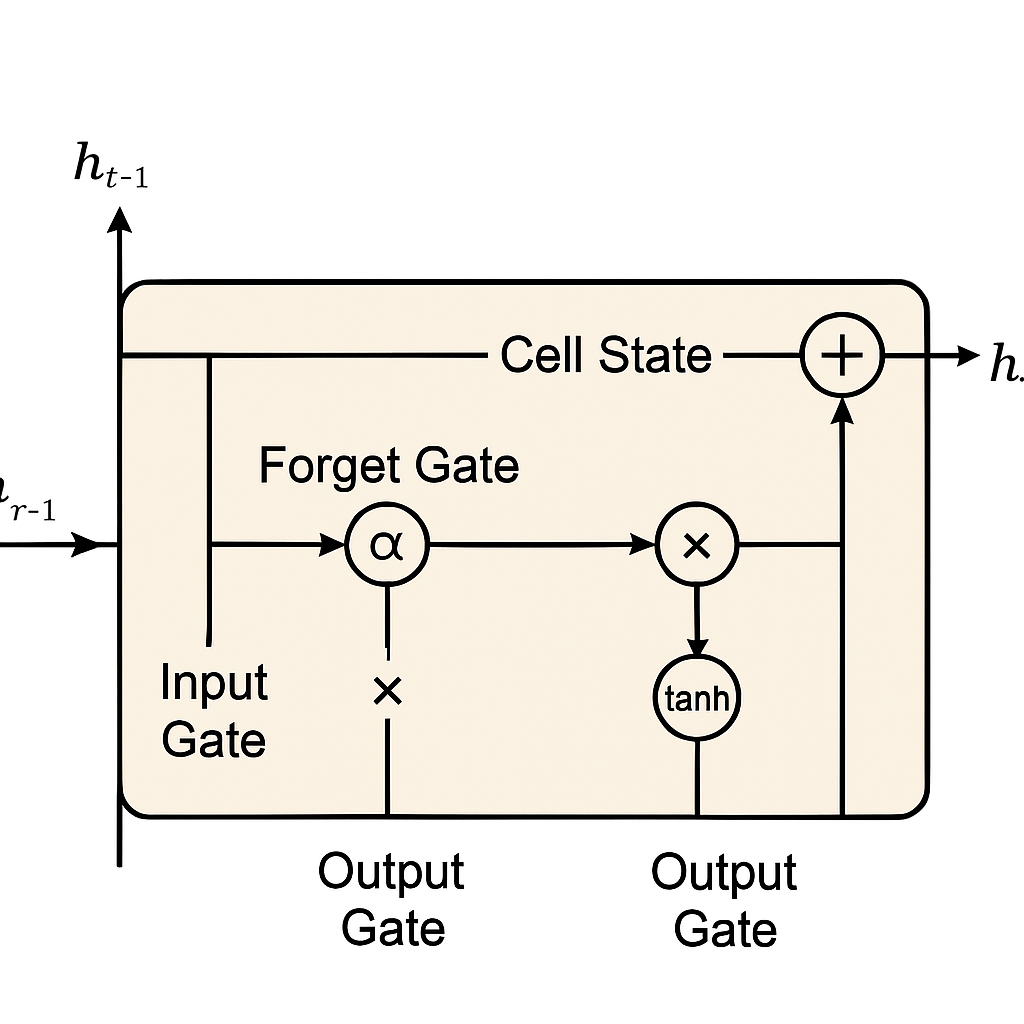
LSTMs address this limitation through a sophisticated gating mechanism that controls the flow of information. An LSTM cell consists of:
The mathematical representation of an LSTM cell at time step t can be expressed as:
Forget Gate:
f_t = σ(W_f · [h_{t-1}, x_t] + b_f)
Input Gate:
i_t = σ(W_i · [h_{t-1}, x_t] + b_i)
g_t = tanh(W_g · [h_{t-1}, x_t] + b_g)
Cell State Update:
C_t = f_t * C_{t-1} + i_t * g_t
Output Gate:
o_t = σ(W_o · [h_{t-1}, x_t] + b_o)
h_t = o_t * tanh(C_t)
Where:
Bidirectional LSTMs process sequences in both forward and backward directions, allowing the network to capture patterns that depend on both past and future information. This is particularly useful in applications where the entire sequence is available during inference, such as natural language processing tasks.
Multiple LSTM layers can be stacked on top of each other to create deeper networks capable of learning more complex patterns. Each layer captures patterns at different levels of abstraction, similar to how convolutional layers work in CNNs.
LSTMs are trained using a modified version of backpropagation called Backpropagation Through Time (BPTT). This algorithm unfolds the recurrent network through time and applies standard backpropagation to compute gradients.
To prevent exploding gradients, a common issue in recurrent networks, gradient clipping is often employed. This technique restricts gradient values to a predefined range, ensuring stable training.
When training on sequences of variable length, padding and masking techniques ensure that the model properly handles shorter sequences without being influenced by padding values.
LSTMs benefit from various regularization techniques:
LSTMs excel at time series forecasting tasks across domains:
In NLP, LSTMs are used for:
LSTMs form the backbone of many speech recognition systems, helping to:
The ability to learn normal patterns in sequential data makes LSTMs valuable for:
GRUs simplify the LSTM architecture by combining the forget and input gates into a single "update gate" and merging the cell state and hidden state. GRUs are computationally more efficient while maintaining comparable performance on many tasks.
Peephole LSTMs allow gate layers to look at the cell state, providing more fine-grained control over the flow of information.
Attention mechanisms have been integrated with LSTMs to allow the model to focus on different parts of the input sequence when producing outputs. This combination has shown significant improvements in machine translation and other sequence-to-sequence tasks.
ConvLSTM replaces the fully connected matrices in standard LSTMs with convolutional structures, making them more suitable for spatiotemporal data like video sequences and weather radar images.
Effective time series prediction with LSTMs requires careful data preparation:
Feature engineering for time series LSTM models includes:
When designing LSTM models for time series prediction:
Critical hyperparameters to tune include:
Common metrics for evaluating LSTM time series models include:
Time series data requires specialized cross-validation approaches:
LSTM performance should be compared against:
This case study explores using LSTMs to predict stock prices by incorporating technical indicators, market sentiment data, and related asset prices.
LSTMs can effectively predict energy consumption patterns by learning from historical usage data, weather conditions, and seasonality factors.
This example demonstrates how LSTMs can be used for sentiment analysis and text classification tasks, showing their effectiveness in capturing linguistic patterns.
LSTMs are computationally intensive, requiring substantial resources for training on large datasets or long sequences.
With small datasets, LSTMs can easily overfit, necessitating proper regularization and data augmentation techniques.
The black-box nature of LSTMs makes it challenging to interpret predictions, which can be problematic in regulated industries or critical applications.
Transformer architectures have begun to replace LSTMs in many NLP tasks, though LSTMs remain competitive for many time series applications.
Combining LSTMs with attention mechanisms, transformers, or physics-informed neural networks shows promise for enhanced performance.
Distributing LSTM training across devices while preserving privacy is an emerging research area with applications in healthcare and IoT.
Implementing LSTMs on neuromorphic hardware could lead to significant efficiency improvements for edge computing applications.
Research into quantum implementations of LSTM algorithms could potentially overcome computational limitations for extremely large datasets.
LSTM networks remain a powerful tool for sequential data modeling and prediction despite the emergence of newer architectures. Their ability to capture long-term dependencies makes them particularly valuable for time series forecasting, natural language processing, and other sequence modeling tasks.
The continuing evolution of LSTMs through variants and hybrid approaches ensures their relevance in modern deep learning applications. As computational resources improve and algorithms advance, we can expect further refinements and broader applications of these versatile neural network architectures.