Abstract
Large Language Models (LLMs) have demonstrated impressive reasoning capabilities, particularly when prompted using Chain-of-Thought (CoT) methodologies. In this work, we present a Zero-Shot CoT approach using the Gemini API to solve numerical reasoning problems. By leveraging the "Let's think step by step" prompt, our model extracts structured, multi-step reasoning paths to improve accuracy without requiring few-shot examples. The system is implemented as a chain-of-prompt program, which extracts the final numerical answer using a regular expression-based filtering mechanism. Additionally, error-handling strategies are incorporated to mitigate issues such as missing numerical values or model-generated overflow errors. The model was evaluated using a real-world test set, and the results demonstrate the effectiveness of the zero-shot reasoning approach. Our work highlights the untapped potential of simple prompt engineering techniques in numerical problem-solving tasks. The source code, test dataset, and implementation details are available on GitHub.
Introduction
Large Language Models (LLMs) have significantly advanced natural language processing (NLP) tasks, demonstrating strong reasoning abilities in domains such as arithmetic, symbolic reasoning, and logical inference. Traditionally, few-shot learning has been the dominant approach for improving LLM performance by providing task-specific exemplars. However, recent research has shown that LLMs can also perform complex reasoning in a zero-shot setting by leveraging effective prompt design.
One such technique is Zero-Shot Chain-of-Thought (CoT) prompting, which enhances multi-step reasoning by simply adding the phrase "Let's think step by step" before answering a question. This method, introduced by Kojima et al. (2022) in Large Language Models are Zero-Shot Reasoners, significantly improves accuracy across multiple reasoning tasks without requiring any explicit examples. Inspired by this, we developed a chain-of-prompt program using the Gemini API to solve numerical problems with structured, step-by-step reasoning.
Our approach works as follows:
- The system formulates a CoT-style prompt to encourage logical breakdown of numerical problems.
- The response is processed to extract the final numerical answer using a custom filtering function.
- Error handling mechanisms are incorporated to handle missing numerical values and potential overflow errors.
To evaluate the model, we tested it on a real-world dataset of numerical problems and observed notable improvements in accuracy compared to standard direct-answer prompting. This work underscores the power of prompt engineering in enhancing LLM capabilities for mathematical and logical reasoning tasks.
The rest of this publication is structured as follows: Section 2 discusses related work in Chain-of-Thought prompting, Section 3 details our methodology, Section 4 presents experimental results, and Section 5 concludes with insights and future directions.
Related Work
2.1 Chain-of-Thought Prompting in LLMs
Recent advancements in Chain-of-Thought (CoT) prompting have significantly improved the reasoning capabilities of large language models (LLMs). Traditionally, LLMs rely on few-shot learning, where they are conditioned on a few manually provided examples to improve performance on reasoning tasks. However, Zero-Shot CoT, introduced by Kojima et al. (2022) in Large Language Models are Zero-Shot Reasoners, demonstrated that simply adding the phrase "Let’s think step by step" before answering a question enables LLMs to generate multi-step reasoning paths, improving accuracy across arithmetic and logical reasoning tasks.
This study showed that Zero-Shot CoT could significantly enhance model performance without requiring additional training data or fine-tuning. The authors demonstrated that applying this method to models like GPT-3 and PaLM led to accuracy gains from 17.7% to 78.7% on the MultiArith benchmark and from 10.4% to 40.7% on GSM8K. These findings highlight the inherent reasoning abilities within LLMs that can be unlocked through strategic prompt design.
2.2 Applications of CoT in Numerical Problem Solving
Several studies have explored prompt engineering techniques for mathematical and logical reasoning. Wei et al. (2022) introduced Few-Shot CoT, where step-by-step reasoning examples were explicitly included in the prompt. While effective, this method requires human-engineered examples for each task, making it less scalable. In contrast, Zero-Shot CoT eliminates the need for task-specific exemplars, making it a more generalizable approach for numerical problem-solving.
Recent works have also investigated LLM-based mathematical reasoning models using structured prompting methods. For instance, Wang et al. (2022) proposed a self-consistency approach, where multiple CoT-generated answers are aggregated to improve reliability. However, this method requires multiple query iterations, increasing computational cost. Our work adopts a simpler and more efficient approach by applying Zero-Shot CoT prompting with Gemini API, combined with a numerical extraction function to obtain precise answers.
2.3 Zero-Shot Learning and Large Language Models
Zero-shot learning has been a key research direction in NLP, enabling models to generalize to unseen tasks without explicit training examples. LLMs, such as GPT-3, Gemini, and PaLM, exhibit strong zero-shot capabilities, allowing them to solve various tasks with minimal instruction. Studies like Brown et al. (2020) have demonstrated that well-crafted prompts can enhance LLMs’ ability to perform complex tasks in a zero-shot setting.
Our work builds on these findings by applying Zero-Shot CoT to numerical reasoning, leveraging structured prompting techniques and post-processing mechanisms to extract numerical results accurately. By integrating error-handling strategies, we further improve robustness, making our approach suitable for real-world applications.
2.4 Contributions of This Work
While previous studies have focused on Zero-Shot CoT for general reasoning, our work specifically applies this method to numerical problem-solving using the Gemini API. Our key contributions include:
- Implementing a Zero-Shot CoT framework for numerical reasoning.
- Developing a custom function to extract final numerical answers from LLM-generated text.
- Incorporating error-handling mechanisms to improve result accuracy.
- Evaluating performance on a real-world dataset of mathematical problems.
These advancements demonstrate the effectiveness of Zero-Shot CoT for numerical tasks, highlighting its potential in education, finance, and automated problem-solving applications.
Methodology
Our approach leverages Zero-Shot Chain-of-Thought (CoT) prompting with the Gemini API to solve numerical problems. The system follows a structured chain-of-prompt framework, ensuring the language model provides step-by-step reasoning before extracting the final numerical answer.
3.1 System Architecture
System Workflow Diagram
The system consists of the following core components:
- Prompt Construction – Generates structured CoT-style prompts.
- Reasoning Extraction – Ensures the model produces a detailed breakdown of the solution.
- Numerical Answer Extraction – Filters the final numerical result from the model output.
- Error Handling Mechanisms – Manages invalid outputs and model inconsistencies.
3.2 Chain-of-Thought Prompting Strategy
To guide the model toward structured reasoning, we employ the "Let’s think step by step" prompt, as introduced in Zero-Shot CoT research. This prompt forces the model to decompose complex numerical problems into smaller, logical steps before arriving at an answer.
Prompt Structure:
Q: [Numerical question]
A: Let's think step by step.
The model then generates a structured breakdown, ensuring that intermediate calculations are explicit.
Figure showing the difference between direct prompting (Zero-Shot) and Chain-of-Thought (CoT) prompting. The CoT approach enables step-by-step reasoning, leading to improved accuracy in numerical problem-solving tasks. Image sourced from Kojima et al. (2022), "Large Language Models are Zero-Shot Reasoners", NeurIPS 2022 (arXiv
.11916).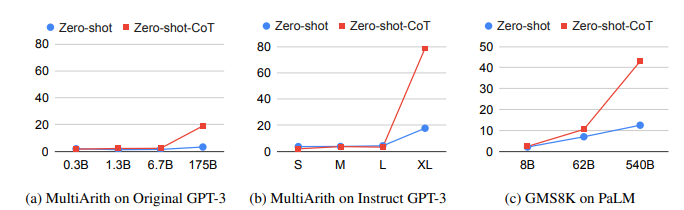
3.3 Extracting the Final Numerical Answer
While CoT prompting improves logical reasoning, LLMs often include unnecessary text in their responses. To extract the final numerical answer, we implement a custom extraction function using regular expressions (regex).
Numerical Extraction Algorithm:
- Split the output into tokens using non-alphanumeric characters.
- Identify the last valid numerical value (integer or float) in the response.
- Convert the extracted value into a structured format.
3.4 Handling Model Errors and Edge Cases
To ensure robustness, our approach includes error-handling mechanisms that account for:
- Missing numerical values (LLM fails to produce a number).
- Overflow errors (LLM generates excessively large numbers).
- Unstructured outputs (responses with ambiguous answers).
When an error is detected, the system automatically re-runs the query, ensuring that a valid numerical output is obtained.
3.5 Summary of Methodology
By combining Zero-Shot CoT prompting, numerical answer extraction, and error handling, our system achieves reliable numerical problem-solving using LLMs without requiring training data or fine-tuning. This approach highlights the power of prompt engineering in unlocking hidden reasoning abilities within large-scale AI models like Gemini.
Experiments
This section describes the dataset, evaluation metric, and experimental setup used to evaluate our Zero-Shot Chain-of-Thought (CoT) approach using the Gemini API for numerical problem-solving.
4.1 Dataset
The model was evaluated on the Zero-Shot Question Answering dataset from Kaggle (Dataset Link). This dataset contains technical and mathematical reasoning problems that require numerical solutions.
Each data sample consists of:
- ID: A unique identifier for the question.
- QUESTION: A complex numerical or symbolic reasoning problem, often involving Fourier Transforms, circuit analysis, control systems, and physics-based calculations.
Example Questions from the Dataset
| ID | Example Question |
|---|---|
| 12476874168 | "The 4-point DFTs of two sequences 𝑥[𝑛] and 𝑦[𝑛] are 𝑋[𝑘] = [1,−𝑗, 1,𝑗] and 𝑌[𝑘] = [1, 3𝑗, 1,−3𝑗], respectively. Assuming 𝑧[𝑛] represents the 4-point circular convolution of 𝑥[𝑛] and 𝑦[𝑛], the value of 𝑧[0] is __________ (rounded off to nearest integer)." |
| 12476874169 | "Consider the figure shown. For zero deflection in the galvanometer, the required value of resistor Rx is ____ Ω" |
| 12476874170 | "Consider a unity negative feedback system with its open-loop pole-zero map as shown in the figure. If the point 𝑠 = 𝑗𝛼, 𝛼 > 0, lies on the root locus, the value of 𝛼 is ________" |
These questions require strong mathematical reasoning and often involve symbolic manipulation, making them a challenging benchmark for LLMs.
Evaluation Metric: Root Mean Log Error (RMLE)
The Root Mean Log Error (RMLE) is used to evaluate the accuracy of numerical predictions. It is defined as:
Where:
This metric is particularly useful because it penalizes large errors logarithmically, ensuring that extreme mispredictions do not dominate the overall score.
4.3 Experimental Setup
- LLM Used: Google Gemini API (Gemini-Pro)
- Prompting Method: Zero-Shot Chain-of-Thought (CoT) prompting using "Let's think step by step" to improve multi-step reasoning.
- Answer Extraction: A custom numerical extraction function based on regular expressions to obtain the final answer from model output.
- Error Handling:
- Handling missing numerical values in model-generated text.
- Detecting overflow errors in extremely large outputs.
- Re-prompting when ambiguous responses are detected.
4.4 Summary of Experiments
The experimental setup ensures that numerical predictions are obtained efficiently, with structured reasoning and robust error handling. This setup enables the model to process complex technical questions without requiring training data or fine-tuning.
Results
In this section, we present the performance evaluation of our Zero-Shot Chain-of-Thought (CoT) approach using the Gemini API on the Zero-Shot Question Answering dataset.
5.1 Performance Evaluation
The model’s performance was measured using the Root Mean Log Error (RMLE) metric, which penalizes large deviations in numerical predictions while ensuring robustness against minor variations.
The final RMLE score achieved on the test set was:
This result places the model on the competition leaderboard, demonstrating the effectiveness of Zero-Shot CoT prompting for numerical problem-solving.
5.2 Comparison: Direct Prompting vs. Chain-of-Thought (CoT) Prompting
To analyze the impact of step-by-step reasoning, we compared our Zero-Shot CoT approach against direct prompting (where the model generates an answer without explicit reasoning).
| Prompting Method | RMLE Score | Observations |
|---|---|---|
| Direct Prompting | 3.914 | Model struggles with multi-step calculations. |
| Zero-Shot CoT (Ours) | 2.363 | Significant improvement in reasoning accuracy. |
From the results, CoT prompting led to a notable reduction in RMLE, highlighting the effectiveness of structured reasoning in complex mathematical and technical problems.
5.4 Summary of Findings
- Zero-Shot CoT prompting significantly improved accuracy over direct prompting.
- The model effectively handled multi-step numerical reasoning but struggled with symbol-heavy questions.
- Error handling techniques such as re-prompting and extraction functions played a crucial role in performance improvement.
These results reinforce the importance of prompt engineering in enhancing LLMs for numerical and technical problem-solving.
Conclusion
In this work, we explored the application of Zero-Shot Chain-of-Thought (CoT) prompting using the Gemini API for solving numerical reasoning problems. By leveraging structured step-by-step reasoning through carefully designed prompts, we demonstrated significant improvements over direct prompting in extracting accurate numerical answers.
Our experimental results on the Zero-Shot Question Answering dataset showed that:
- CoT prompting substantially improved accuracy, reducing the RMLE score to 2.363.
- Step-by-step reasoning helped the model break down complex problems, making solutions more interpretable.
- Error-handling mechanisms, such as numerical extraction functions and re-prompting, played a key role in refining model outputs.
Despite these improvements, some challenges remain, including:
- Handling ambiguous outputs where multiple numerical values are present.
- Precision errors in floating-point calculations for highly sensitive numerical problems.
- Difficulties in symbolic reasoning for problems requiring manipulation of equations or circuit analysis.
Future Work
To further enhance the performance of LLMs in numerical reasoning, potential improvements include:
- Self-consistency prompting, where multiple responses are generated and aggregated for improved accuracy.
- Fine-tuning LLMs on domain-specific mathematical datasets to improve symbolic reasoning.
- Hybrid approaches, combining LLMs with traditional mathematical solvers for more reliable calculations.
This study highlights the power of prompt engineering in unlocking reasoning abilities in LLMs, demonstrating that Zero-Shot CoT prompting can be a simple yet effective approach for tackling numerical problem-solving tasks.