# Disclaimer In this work we porpose a cyber-physical systems-based approach for intelligent energy resource management in electric vehicle charging network. A collaborative multi-agent system has been developed where electric vehicle (EV) charging stations coordinate on the power to be delivered to vehicles using epidemic protocols. This approach ensures that the power output does not exceed the availability of the electric grid, optimizing energy distribution and enhancing the overall efficiency of the charging network. For the complete paper, please refer to the PDF file (PowerSyncSystem.pdf) attached to this page or click [here](https://www.linkedin.com/posts/gabriele-ciccotelli_a-study-of-chaos-engineering-based-on-hybrid-activity-7192518254492336128-pzTE?utm_source=share&utm_medium=member_desktop&rcm=ACoAACvNlpcBcNa_7cjCF6YUGXLyW8nBcaSKm7A). Full code [here](https://github.com/G-R-Dual-Mind-Lab/PowerSync_System) on GitHub. Italian explaination of the project at this [link](https://youtu.be/PXA5ZWf2lyY?si=FL0WJSyOZ2MgRtqE) on YouTube. 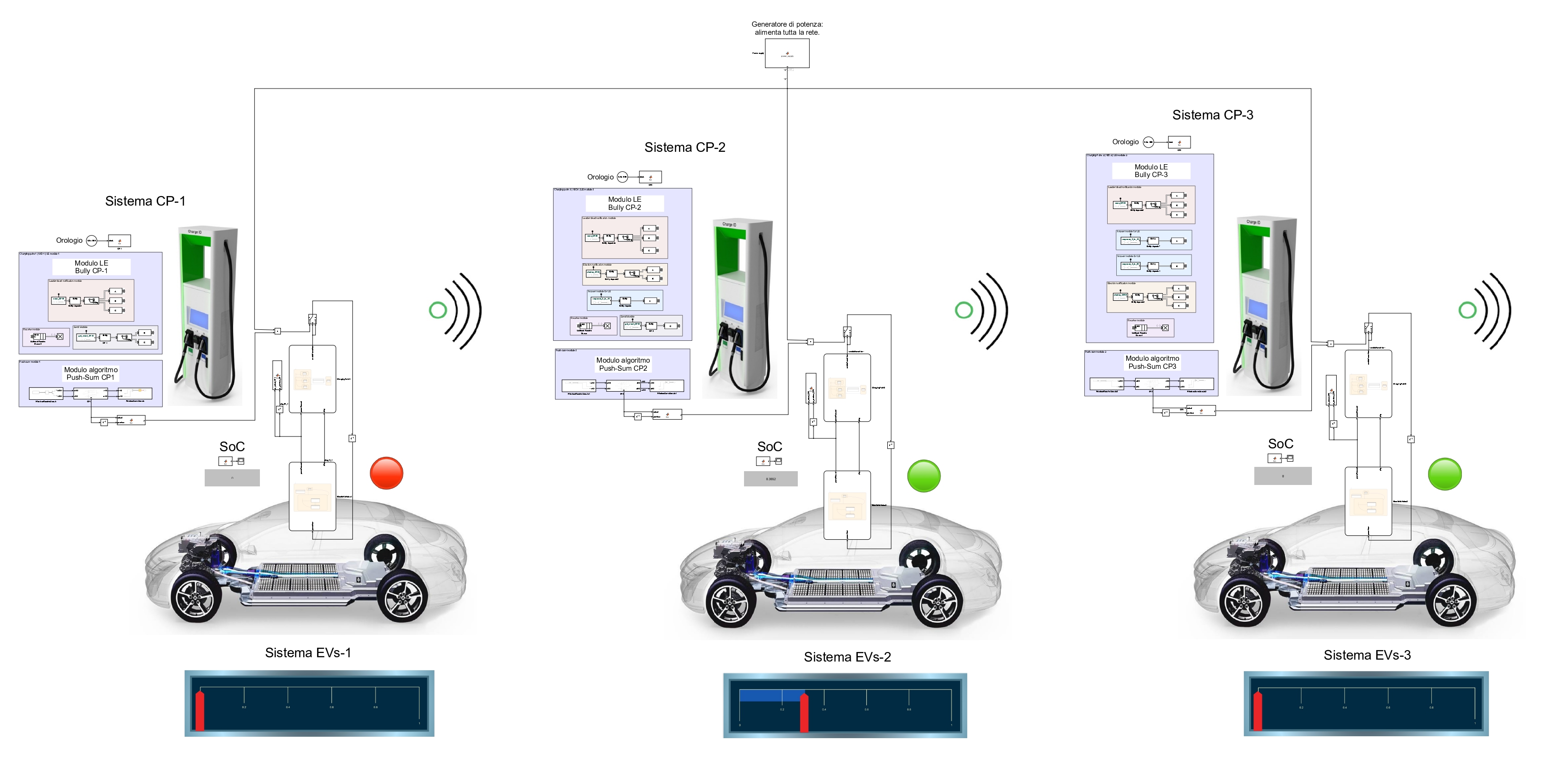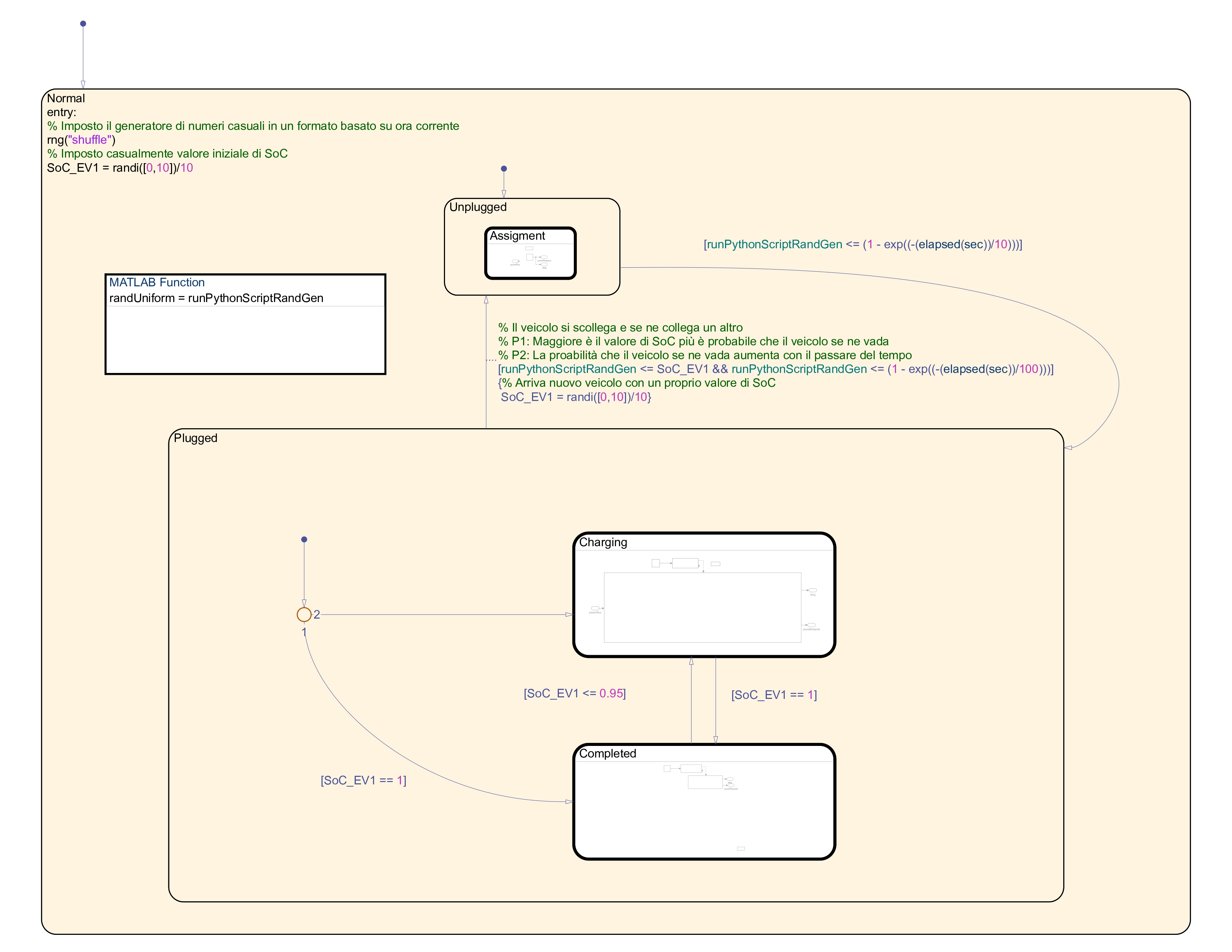The figure below shows Simulink and Stateflow diagram of the complete system. ![SIM_SCHEMA_page-0001.jpg](SIM_SCHEMA_page-0001.jpg) # Authors **[Ciccotelli Gabriele](https://www.linkedin.com/in/gabriele-ciccotelli/)**, **[Iuliano Roberto](https://www.linkedin.com/in/robertoiuliano/)** # Abstract In a context where electric vehicle (EV) adoption is rapidly increasing, the need for efficient energy resource management has become crucial. This study proposes a solution to optimise power delivery at EV charging stations, based on the integration of leader election algorithms and distributed computing. The solution developed and presented in this work represents a concrete application of the fundamental concepts in the modelling and analysis of cyberphysical systems (CPS) to enhance the efficiency of charging infrastructures, with potential benefits for sustainability and intelligent grid management. # Introduction The growing adoption of electric vehicles (EVs) presents new challenges for energy resource management, particularly in handling power flows to charging stations. It is essential to ensure that power is distributed efficiently and proportionally among the various stations to avoid overloads and maintain acceptable charging times for all users. To address this problem, several solutions have been explored that leverage the potential of cyber-physical systems—systems combining physical processes and computational elements to solve complex problems. In this context, an approach based on leader-election and distributed computing algorithms is proposed to optimise power distribution among charging stations. The proposed method utilises a particular leaderelection algorithm known as the Bully algorithm. The purpose of this algorithm is to identify the station with the highest unique identifier (UID) and designate it as the leader. Subsequently, based on this election, numerical values are assigned to each charging point, which are then employed by the Push-Sum algorithm to calculate the power share to be delivered from the generator at any given time. This document will provide a detailed analysis of the proposed solution’s implementation, aiming to ensure fair and dynamic energy management across EV charging networks. # Scenario of Interest Consider a scenario featuring a network of n charging points (CP) for electric vehicles, all powered by a common generator. Each CP can only connect to one EV at a time, allowing the EV to charge its battery by drawing power from the generator. This system can be framed as a cyber-physical system (CPS), as well as a real-time system that must respond to external stimuli within specified time constraints. Similarly, each charging point can be viewed as an individual CPS, characterised by a network module enabling it to communicate through message exchange with other charging points in the system. This communication method allows the CPs to coordinate and calculate the power quotas from the shared generator within a certain time limit. At any given moment, each CP’s power quota must match the ratio of the generator’s total output to the number of CPs currently connected to vehicles requesting power. To implement this solution, two algorithms commonly referenced in distributed computing literature were selected: - The Bully Algorithm: This algorithm is typically used for leader election within a network of computational nodes; - The Push-Sum Algorithm: Usually employed for computing aggregates, such as averages, in a distributed system. The Push-Sum algorithm was selected to calculate the distributed power quotas. Specifically, this algorithm calculates the proportion of total available power each CP can receive based on its status and the total number of active CPs at that time. For this, the network must start from a state where only one active CP node has a numerical value of 1, while all others are at zero. The Push-Sum algorithm then averages these values, and this calculation is repeated each time there’s a state change in the network (e.g., a vehicle connecting or disconnecting, or a battery reaching full charge). To establish this initial condition, the Bully algorithm was used to assign the leader node in the network a value of 1, leaving the other nodes at zero. ## Requirements Elicitation It is necessary to identify a system that efficiently manages the distribution of power among various charging points for electric vehicles, powered by a common generator. The system must satisfy the following constraints: - Charging Point Management: The system must support a network of charging points, each capable of serving a single electric vehicle at a time. Only active CPs, meaning those connected to a vehicle that requires power, should draw energy from the network. - Power Distribution: The generator’s power should be evenly divided among the CPs connected to a vehicle that requires power. At any moment, the power supplied to each of these CPs should equal the total available power divided by the number of CPs connected to a vehicle being charged. - Coordination Between Charging Points: Whenever there is a state change in the network, active CPs must communicate to automatically recalculate the power quotas, adjusting to the new conditions. - Charging Conditions: - A vehicle may only receive power if it is connected to a charging point. - A vehicle with a fully charged battery should no longer receive power. - If a vehicle’s battery reaches full charge (SoC - State of Charge), no power should be supplied to it until the SoC drops below 95%. - A CP that is out of service should not supply power. - Total Power Limitation: At any given time, the sum of the power supplied by all active charging points should never exceed the total power provided by the generator. ## Informal Requirements Definition From the previous analysis, the following functional requirements are derived and described in natural language: - R1: An electric vehicle cannot request power unless it is connected to a charging point. - R2: If a vehicle’s battery is fully charged, it cannot request power. - R3: If a vehicle’s battery level is between 95% and 100% and was previously at 100%, it cannot request power until the State of Charge (SoC) drops below 95%. - R4: The charging point can supply power only if a vehicle is connected. - R5: The charging point cannot supply power if it is out of service. - R6: The charging point supplies power to the vehicle only if the vehicle’s battery is not fully charged. - R7: At any moment, the sum of the power supplied by the charging points must be greater than or equal to zero and should never exceed the total power supplied by the generator. - R8: At any moment, the sum of the power supplied by charging points without connected vehicles must be zero. - R9: Within 4 seconds of the last change in a vehicle’s power request, each active and functioning CP must supply power equal to the generator’s output, divided by the number of active charging points. # Implementation of the Solution The proposed solution is centred on the following mechanisms: - Each CP (or node) is associated with a UID and an initial numerical value $$ v_i $$, set to zero, which will later be used to calculate power quotas through the Push-Sum algorithm: $$ \forall cp_i \in \mathcal{CP}, \; \exists (UID_i \in \mathbb{N}, v_i \in \mathbb{R}) $$ - Nodes connected to a vehicle requiring power form the set of active $$ CPS $$ denoted as $$ CPs_{active} $$. - Only nodes within $$ CPs_{active} $$ participate in the leader election process, managed as follows: - The Bully algorithm is used to identify the leader node, $$ cpleader ∈ CPs_{active} $$, which is the node with the highest UID. This process also sets the leader node’s variable $$ v = 1 $$, while other nodes remain at zero. - The leader election process is initiated whenever a network state change occurs due to any of the following events: - An EV disconnects from the CP to which it was connected. - An EV connects to an available CP and requests power. - The battery of a connected EV reaches full charge. - Immediately after any of the above events, all $$ v_i $$ variables are reset to zero. From these points, it is clear that the Bully algorithm is employed to ensure that, following any of the conditions listed above, only one node in $$ CPs_{active} $$ will have $$ v = 1 $$ within a specific time frame, designating it as the leader. Additionally, it is evident that: - If $$ CPs_{active} = ∅ $$, the election process is not initiated, and all $$ v_i $$ variables remain zero. This process continuously executes the Push-Sum algorithm, which is used to calculate the power quotas assigned to each $$ cpi ∈ CPs_{active} $$. Thus, this algorithm enables the nodes in the network to reach consensus. Once consensus is achieved, each EV connected to a CP can draw power from the charging point, provided the CP is not in an error state. The mechanisms outlined here illustrate the goal of creating a system that avoids overloads and ensures a fair distribution of power to vehicles that request it. # System Model Based on the scenario and approach described in previous sections, a system model was created. A model is a representation of the system, useful for evaluating its properties. It is a good abstraction of the system if it omits only non-essential details. Considering that the identified system combines both continuous and discrete dynamics, it is classified as a hybrid (or modal) system. This classification highlights the coexistence of discrete and continuous characteristics: the system is defined by discrete states, called “modes,” and primarily continuous variables, which determine the system’s evolution. The continuous aspect represents physical processes, such as battery charging and discharging by the EVs and power delivery by the CPs. However, events that characterise the system and cause state transitions, such as the connection or disconnection of vehicles, are discrete and can be described with a state machine. Given this, modal machines were utilised to model this hybrid system. Consequently, it is apparent that the system under consideration is a hybrid event-triggered system. The modelling process followed a well-established engineering principle: complex systems can be described as compositions of simpler subsystems. Therefore, the first phase of this process involved decomposing the domain into multiple subsystems and modelling them accordingly. ## Battery Model: Coulomb Counting Method Simulink diagram of the battery model Coulomb Counting Method (charging phase). ![CCM_carica_page-0001.jpg](CCM_carica_page-0001.jpg) Simulink diagram of the battery model Coulomb Counting Method (discharge phase). 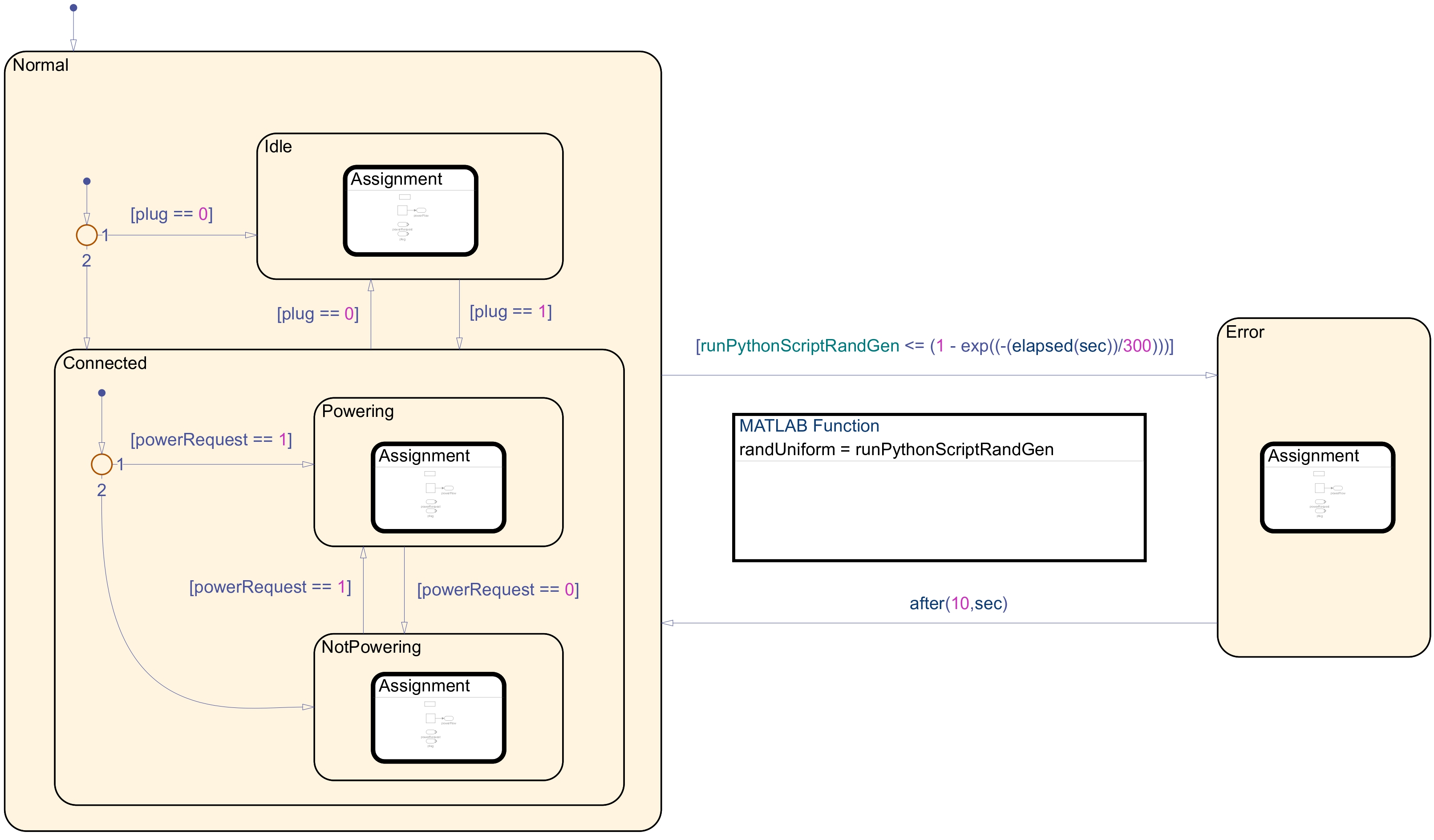![CCM_scarica_page-0001.jpg](CCM_scarica_page-0001.jpg) ## Charging Point Model Model of the charging point system. Above is the actor model. Below is the hierarchical finite-state machine and its mode refinements. Transitions that make the machine non-deterministic are shown in red. The self transition on the Normal state represents a historical transition (labelled H). In the state refinement of the Normal state, the transition from the Connected state to the Idle state is a preemptive transition. 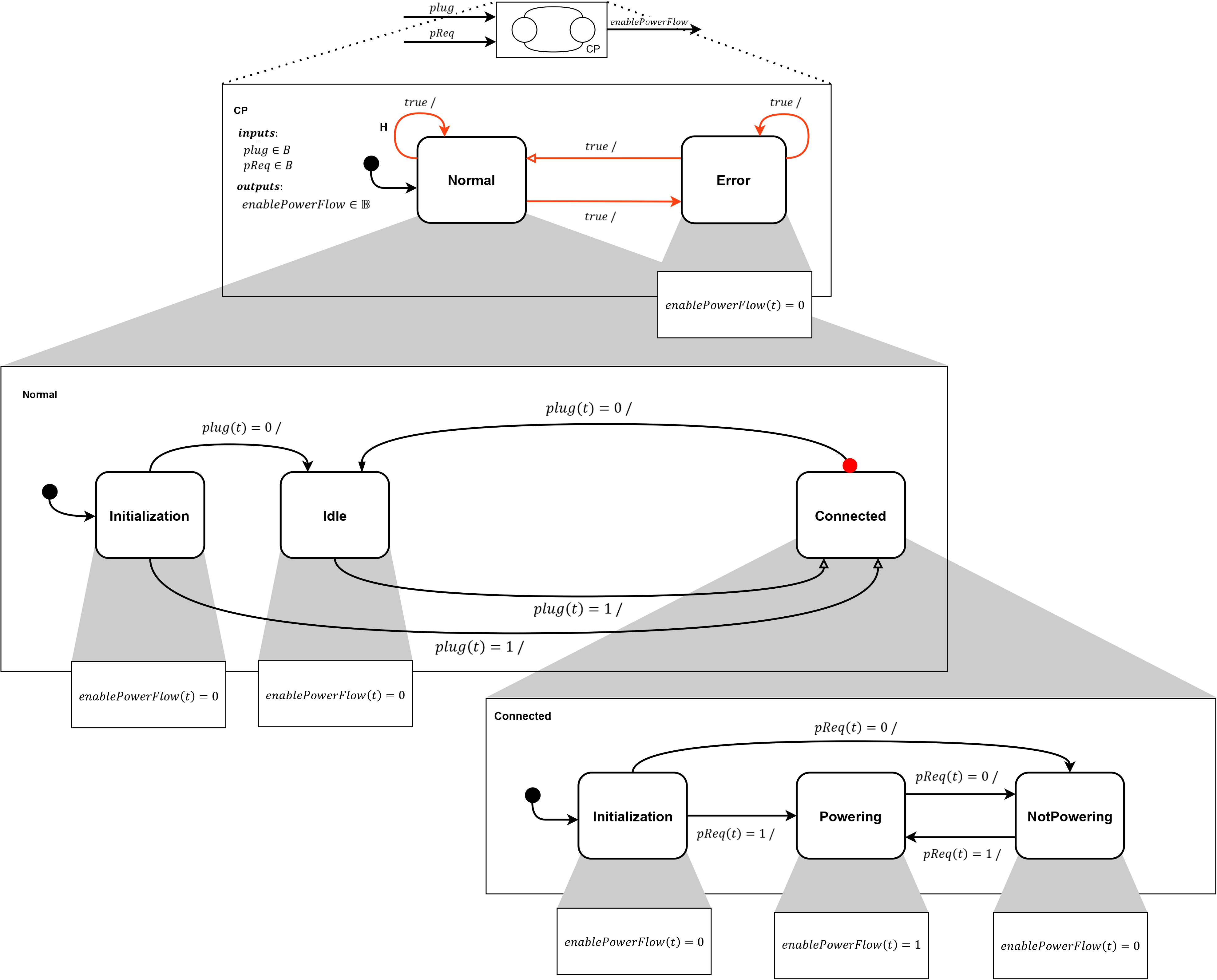![CP_actor_page-0001.jpg](CP_actor_page-0001.jpg) Implementation of the charging point system model in Simulink & Stateflow. ![ImplementazioneCP_page-0001.jpg](ImplementazioneCP_page-0001.jpg) ## Electric Vehicle Model Modal model of the electric vehicle system. The actor model of the system is shown above, while the hierarchical state machine and corresponding refinements of modes are depicted below. Transitions introducing non-determinism are highlighted in ed. The self-transition on the Plugged state represents a historical transition (labelled H). The transition from Unplugged to Plugged is a reset transition. 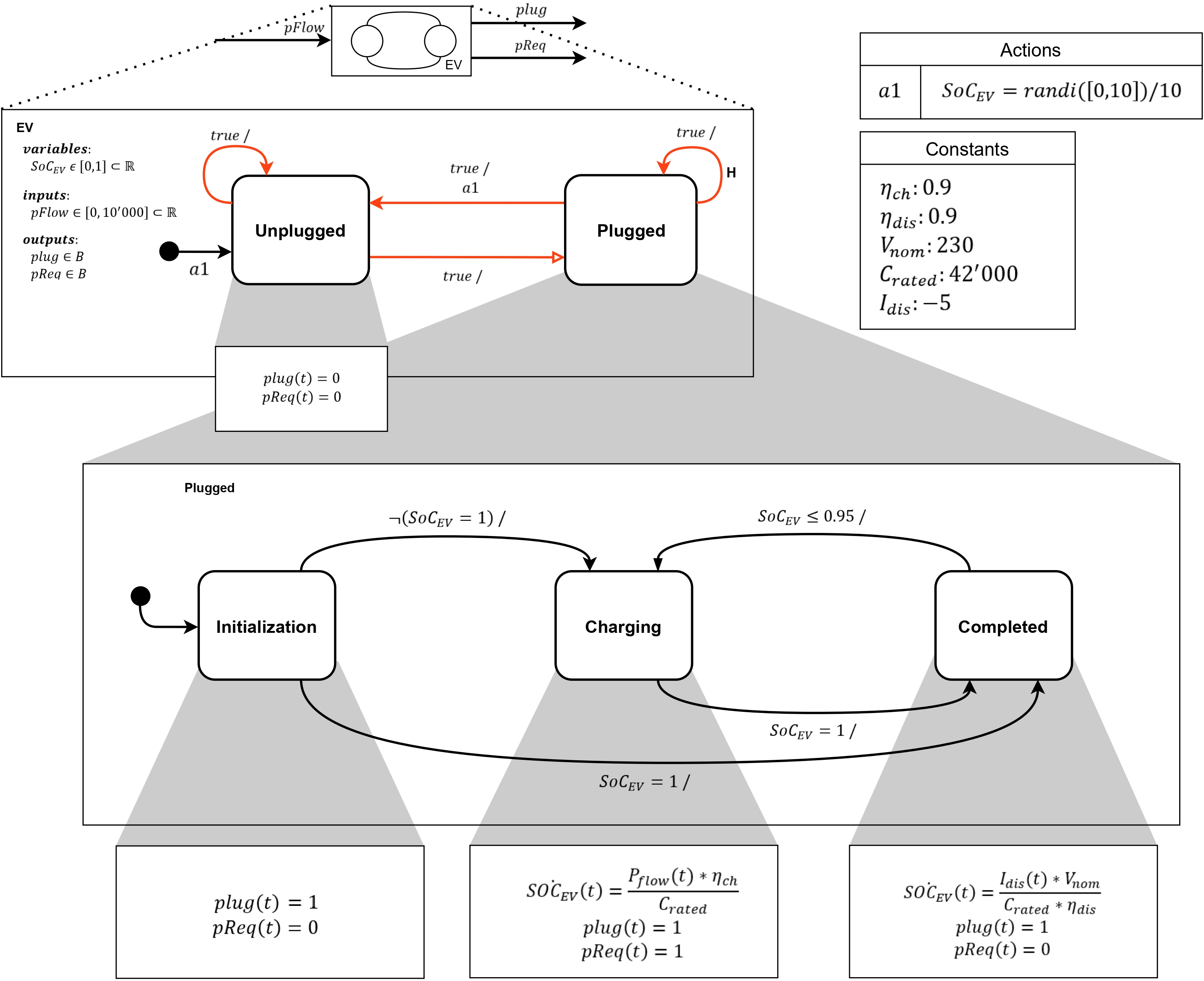![EV_actor_page-0001.jpg](EV_actor_page-0001.jpg) Implementation of the electric vehicle system model in Simulink & Stateflow. ![EV_SS_page-0001.jpg](EV_SS_page-0001.jpg) ## Composition of Electric Vehicle and Charging Point Cascade composition of EV&CP. Model of the synchronous cascade composition of the electric vehicle and charging point systems. ![CCS_EV_CP_page-0001.jpg](CCS_EV_CP_page-0001.jpg) Implementation of the synchronous cascade composition in Simulink Stateflow. ![EV_CP (1)_page-0001.jpg](EV_CP%20(1)_page-0001.jpg) ## Formal Definition of Specifications: Application of Signal Temporal Logic Based on the requirements, and given that the specifications involve the values of continuous signals, the following specifications have been defined using the formalism of Signal Temporal Logic (STL): $$ \begin{align*} \varphi_1 & = G\left\{\left[ plug(t)=0 \right] \implies \left[ pReq(t)=0 \right]\right\} \\ \varphi_2 & = G\left\{ \left[ SoC(t)=1 \right] \implies \left[ pReq(t)=0 \right]\right\} \\ \varphi_3 & = G\left\{\left[ (0.95 \leq SoC(t) \leq 1)\ \mathbf{S}\ (SoC(t^*)=1) \right] \implies \left( pReq(t)=0 \right)\right\} \quad \text{with } t^* < t \\ \varphi_4 & = G\left\{ \left[ enablePowerFlow(t)=1 \right] \implies \left[ plug(t)=1 \right]\right\} \\ \varphi_5 & = G\left\{ \left[ errorState(t)=1 \right] \implies \left[ enablePowerFlow(t)=0 \right]\right\} \\ \varphi_6 & = G\left\{ \left[ enablePowerFlow(t)=1 \right] \implies \left[ SoC(t) \neq 1 \right]\right\} \\ \varphi_7 & = G\left\{ 0 \leq \left[\sum_{i=1}^{n} pFlow_i(t)\right] \leq generatorPower(t) \right\}, \quad n = \text{number of CPs} \\ \varphi_8 & = G\left\{ \left[\sum_{i=1}^{n_{\text{idle}}} pFlow_i(t)\right] = 0 \right\}, \quad n_{\text{idle}} = \text{number of CPs in Idle state} \\ \varphi_9 & = \bigvee_{i=1}^{n} \left[ pReq_i^{\text{actual}}(t) \neq pReq_i^{\text{previous}}(t) \right] \implies F_{[0,4]}\left\{ \bigwedge_{i=1}^{n} \left[ pFlow_i(t) = \frac{generatorPower(t) \cdot poweringState_{CPi}(t)}{n_{CP\_active}} \right] \right\} \end{align*} $$ # Model Implementation in Matlab Simulink & Stateflow After analysing and modelling the various characteristics of the system, its complete implementation was carried out using Simulink and Stateflow tools. Simulink and Stateflow diagram of the complete system. ![SIM_SCHEMA_page-0001.jpg](SIM_SCHEMA_page-0001.jpg) # Experimental Results When designing a system model, such as a cyber-physical system, the primary objective is to enable detailed analysis. The model is not only created to represent the system but also to serve as a tool for performing evaluations that would be impractical or risky to conduct directly on the real system. To this end, various simulations were carried out to assess specific aspects of the system. These simulations allow the analysis of the model’s behaviour under different scenarios and conditions, verifying how the CPS reacts in critical or particularly complex situations. Through these simulations, it is possible to gain a deeper understanding of the system’s performance, safety, and reliability, confirming the validity of the model before its real-world application. In particular, for the case considered, several graphical views of the system’s behaviour were produced and are presented in Figures 1R, 2R, 3R, and 4R. Figure 1R illustrates how the charging points reach consensus concerning the power demands of the vehicles. Graphically, the consensus process is represented by the ”funnel effect,” where the functions progressively converge towards the same final value. It is noted that, in the considered context, consensus is achieved when all active charging points possess the same value, calculated using the Push-Sum algorithm. This value represents the power allocation from the global generator assigned to them. An analysis of the graph reveals that: - The funnel effect lasts longer when the power requests from vehicles to their respective CPs remain unchanged. The funnel effect ceases when there is a change in power requests; - From a performance perspective, it would be desirable to minimise the time required to reach consensus. This is influenced by communication latencies, network topology, and the number of nodes; - The system has a vulnerability: if there is a continuous change in the power request state for a given CP, consensus would never be reached. Technically, this results in the continuous triggering of the Bully Algorithm, causing repeated leader election processes and resetting the estimates calculated by the Push-Sum algorithm. Below is an interpretation of the system’s behaviour during the simulation window from 0s to 5s (Figure 1R). This time window reveals that: - Charging point 1 receives a power request, as indicated by the $$ pReqCP1 $$ signal ”rising”; - Charging point 2 receives a power request, as indicated by the $$ pReqCP2$$ signal ”rising”; - Charging point 3 receives a power request, as indicated by the $$ pReqCP3 $$ signal ”rising”; - After leader election, the estimates from the Push-Sum modules begin to oscillate until consensus is reached (4.5s); - Finally, the system’s behaviour is disrupted by the termination of the power request from the vehicle connected to charging point 1. 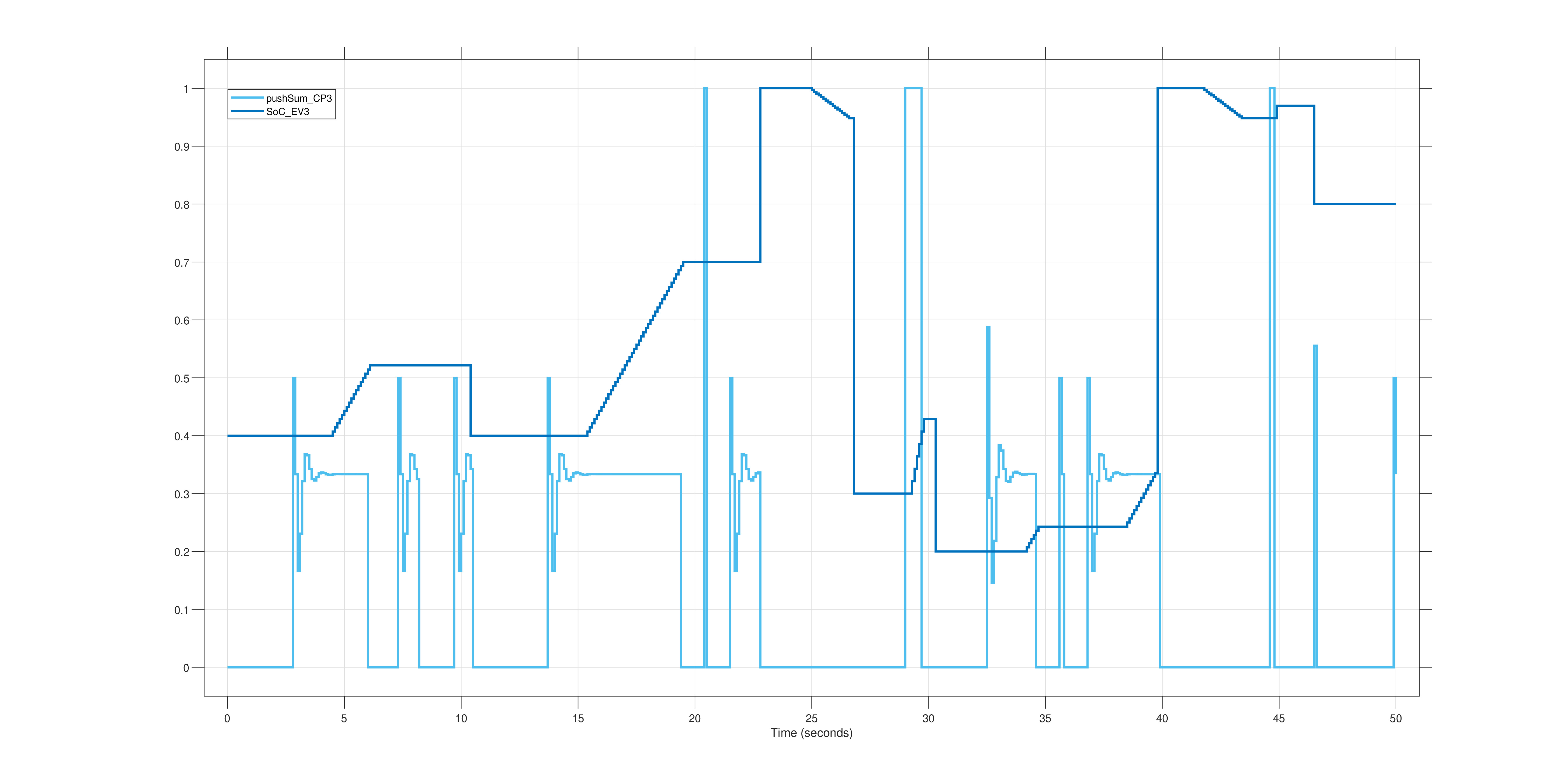Figures 2R, 3R, and 4R show how the SoC of a vehicle connected to a given CP increases during time intervals where consensus is achieved, i.e., when the estimates from the Push-Sum module converge. From an analysis of Figure 4R, the following observations can be made: - At the start of the simulation, the battery charge level is stationary at 40%; - At 4.5s, consensus is achieved, and the SoC begins to increase (the battery charges); - During the next two convergence attempts, consensus Is not reached, causing the SoC to remain stationary at 52%; - Shortly after 10s, a sudden change in the SoC occurs, corresponding to the connection of a new vehicle with a new charge level; - At 15.4s, consensus is achieved, and the battery begins to charge, as seen from the evolution of the SoC; - At 22.8s, a new vehicle is considered, not yet connected to the CP. Its battery charge level is 100%. The vehicle connects to the CP at 25s, but since its SoC is at maximum, no power is supplied, and the battery begins to discharge. Fig. 1R - Graph showing how the charging points reach consensus concerning the power demands of vehicles. The solid lines represent the average value estimates calculated by the Push-Sum modules. The dashed lines represent the power requests. Colours distinguish the different nodes (charging points) in the network. 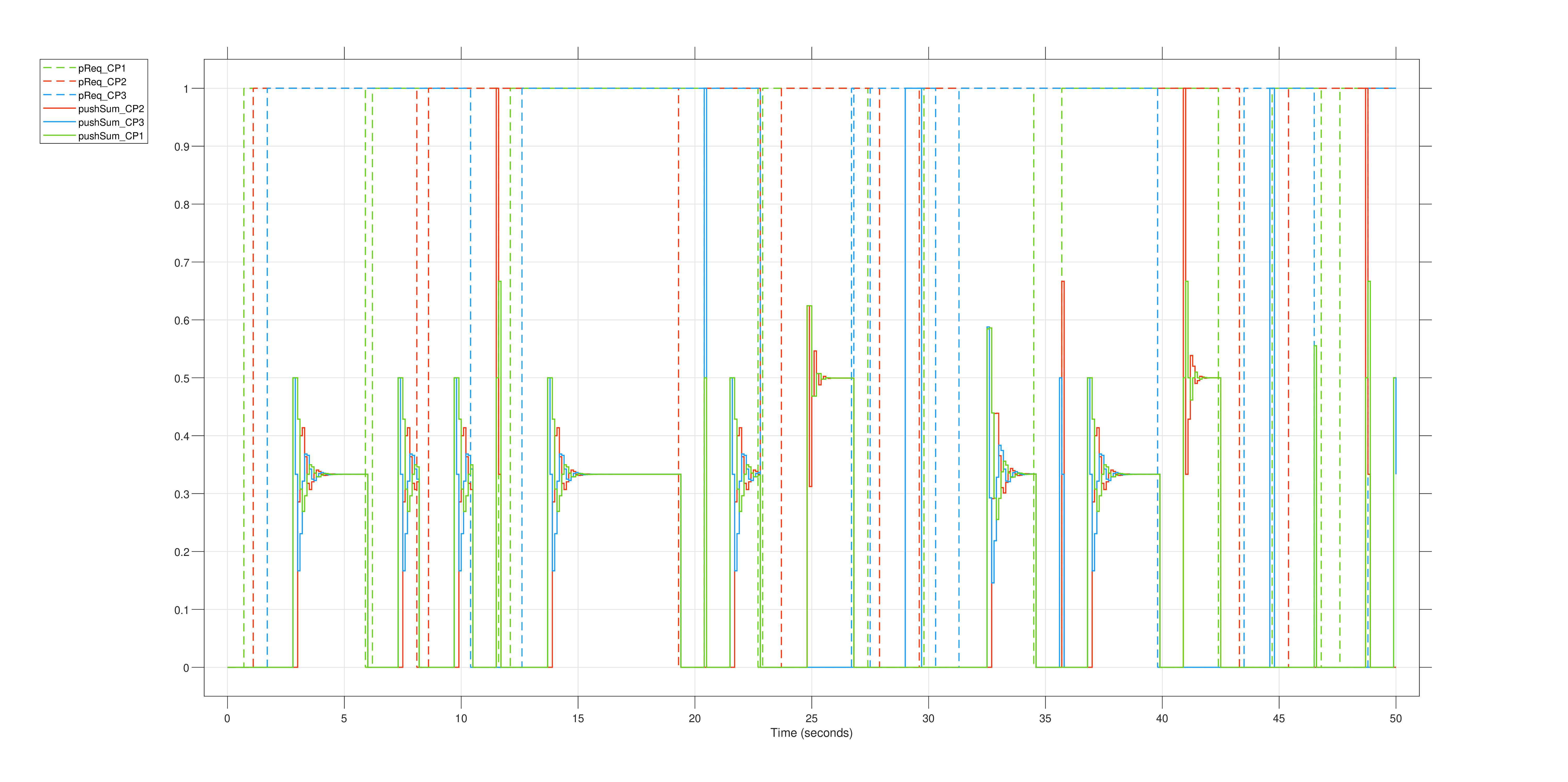![pushSum_pReq.jpg](pushSum_pReq.jpg) Fig. 2R - Graph showing the SoC value of the vehicle connected to CP1 (dark-coloured function) in relation to the average value estimate calculated by the Push-Sum module of charging point 1 (light-coloured function). 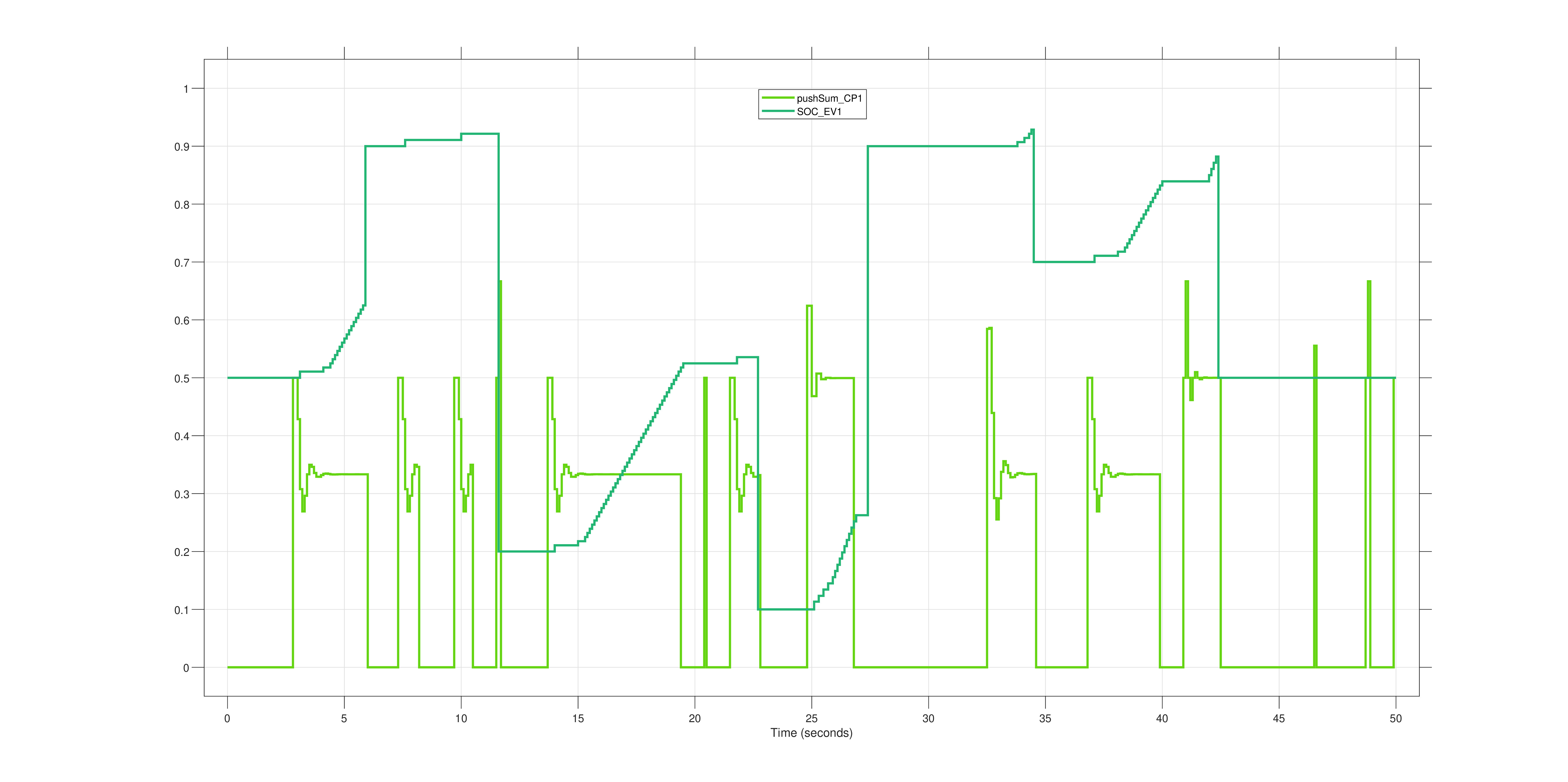![SoC1_pushSum1.jpg](SoC1_pushSum1.jpg) Fig. 3R - Graph showing the SoC value of the vehicle connected to CP2 (dark-coloured function) in relation to the average value estimate calculated by the Push-Sum module of charging point 2 (light-coloured function). 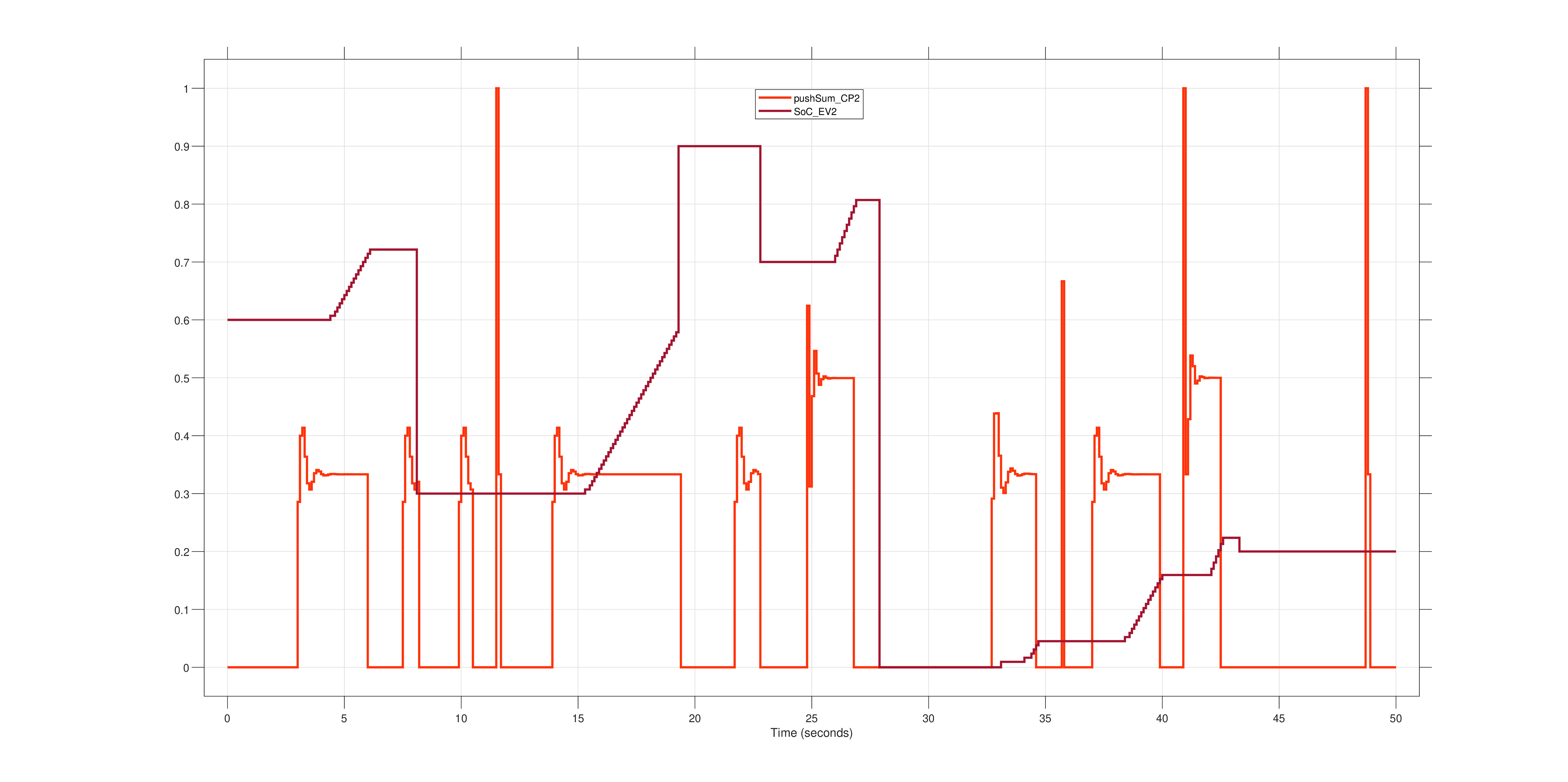![SoC2_pushSum2.jpg](SoC2_pushSum2.jpg) FIG. 4R - Graph showing the SoC value of the vehicle connected to CP3 (dark-coloured function) in relation to the average value estimate calculated by the Push-Sum module of charging point 3 (light-coloured function). ![SoC3_pushSum3.jpg](SoC3_pushSum3.jpg) # Conclusions and Future Work The work discussed in this document allowed for the evaluation of the potential of concepts and knowledge acquired during the ”Analysis and Control of Cyber-Physical Systems” course. During the model implementation phase, the team had to devise solutions to overcome various challenges that arose while applying the theoretical concepts learned. Consequently, the team demonstrated the ability to seek necessary knowledge and apply it to overcome the obstacles encountered, adhering to the philosophy stated at the beginning of the course: ”You can’t teach people everything they need to know. The best you can do is position them where they can and what they need to know when they need to know it. (Seymour Papert)”. Future developments of the proposed solution could address various aspects of the project, including: - Extending the base system models, namely those of the electric vehicle and the charging point, and detailing them according to contextual needs; - Modifying the model implementation to allow for a network of non-homogeneous charging points. Additionally, it would be interesting to evaluate how different network topologies affect the convergence time of the Push-Sum algorithm used to achieve consensus on the power allocations each CP must deliver; - Implementing the dataflow model using alternative solutions to the one employed in this document (Simulink SimEvents library). It was noted that, in complex scheme implementations, the library does not provide sufficient tools to reduce the effort of the implementation process. In conclusion, it is emphasised that the ability to manage complex scenarios was acquired through the knowledge gained. Indeed, despite necessary simplifications, it was possible to structure a solution to a problem that the development team had never encountered before. The entire project, including test files, has been made available on GitHub in a repository accessible [here](https://github.com/G-R-Dual-Mind-Lab/PowerSync_System).