WATER QUALITY POTABILIBITY

What is the Benefits of predicting the water quality?

Information about the features or factors contributing to the quality of water, basically answering the question if the water is portable or not.

From the data prediction,the knowledge of the results derived can help reduce risk in terms of spread of harmful bacterias and diseases.

Visualising the features and prediction results will give more inisght into the data

The features for Predicting Water quality potability and their description is listed below:

ph: pH of 1. water (0 to 14).
Hardness: Capacity of water to precipitate soap in mg/L.
Solids: Total dissolved solids in ppm.
Chloramines: Amount of Chloramines in ppm.
Sulfate: Amount of Sulfates dissolved in mg/L.
Conductivity: Electrical conductivity of water in μS/cm.
Organic_carbon: Amount of organic carbon in ppm.
Trihalomethanes: Amount of Trihalomethanes in μg/L.
Turbidity: Measure of light emiting property of water in NTU.
Potability: Indicates if water is safe for human consumption. Potable means 1 and Not potable 0 ph pH of water
Hardness Capacity of water to precipitate soap in mg/L

Solids Total dissolved solids in ppm

Chloramines Amount of Chloramines in ppm

Sulfate Amount of Sulfates dissolved in mg/L

An Overview of the water prediction can be found here
Link text

#Exploratory Data Analysis and Plotting Libraries

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns


#Plots to appear inside the notebook
%matplotlib inline


#Models from scitkit-learn that will be used for this project
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier


#Model Evaluations libraries
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import precision_score, recall_score, f1_score
from sklearn.metrics import RocCurveDisplay
from sklearn.metrics import roc_auc_score

#Reading into the dataset css file with pandas
df=pd.read_csv("water_potability.csv")

The size of the dataset (rows and columns)
df.shape
(3276,10)

#The top of the data
df.head

From the data displayed we can visually see there are missing values in some rows.

To create a good model and to acheive a better prediction accuracy this missing values has to be filled.

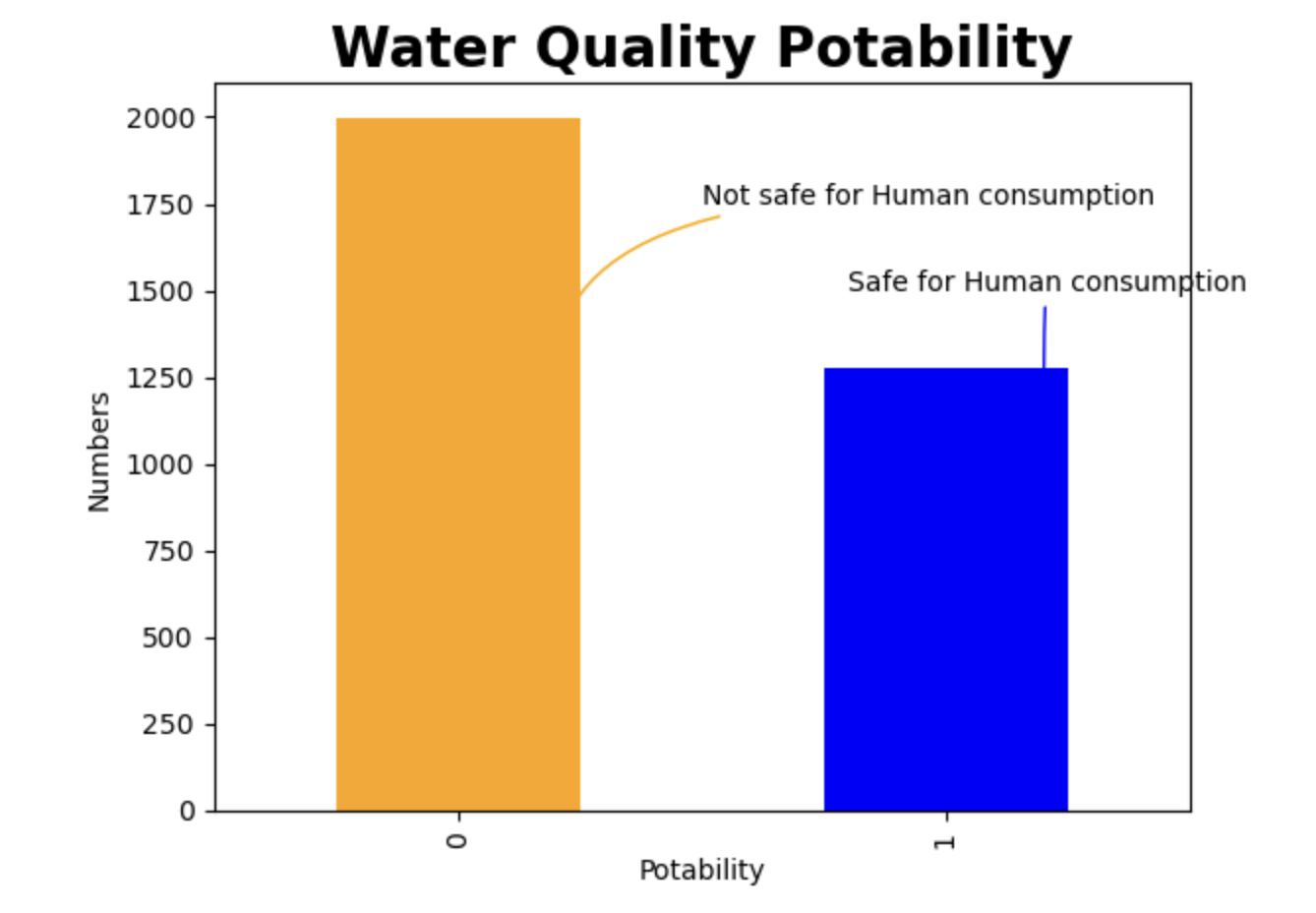
#Lets find out what the total number is in each class (0 and 1) 
df["Potability"].value_counts()

Potability
0    1998
1    1278
Name: count, dtype: int64

#Visualising the the total number in each class (0 and 1) for the Potability Column in the dataset

df ["Potability"].value_counts().plot (kind="bar", color=["orange", "blue"])
plt.title("Water Quality Potability", size=20, weight='bold')
plt.annotate(text="Not safe for Human consumption", xytext=(0.5,1750),xy=(0.2,1250), arrowprops =dict(arrowstyle="->", color='orange', connectionstyle="angle3,angleA=0,angleB=90"), color='black')
plt.annotate(text="Safe for Human consumption", xytext=(0.8,1500),xy=(1.2,1000), arrowprops =dict(arrowstyle="->", color='blue',  connectionstyle="angle3,angleA=0,angleB=90"), color='black')
plt.ylabel("Numbers");

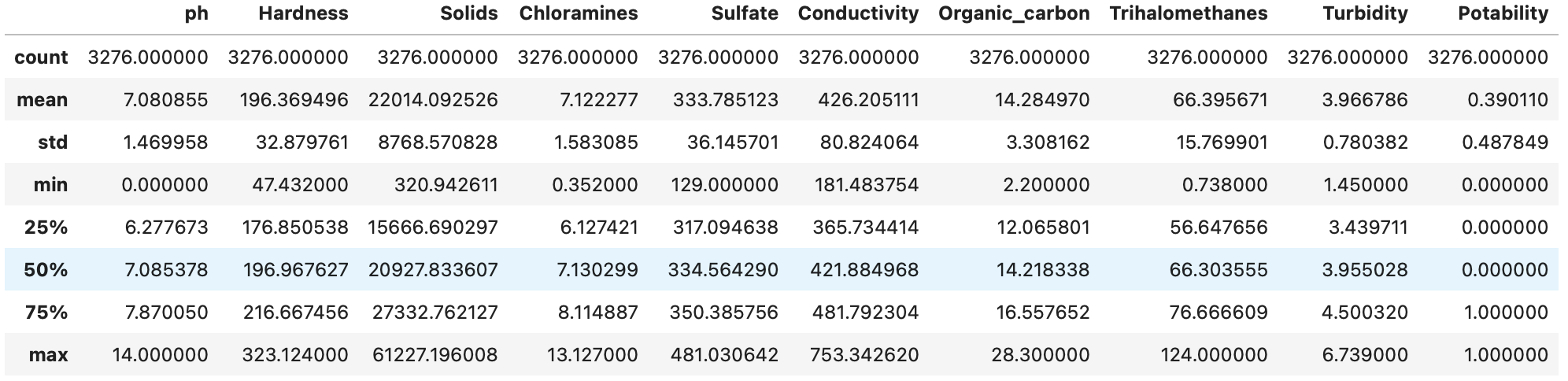
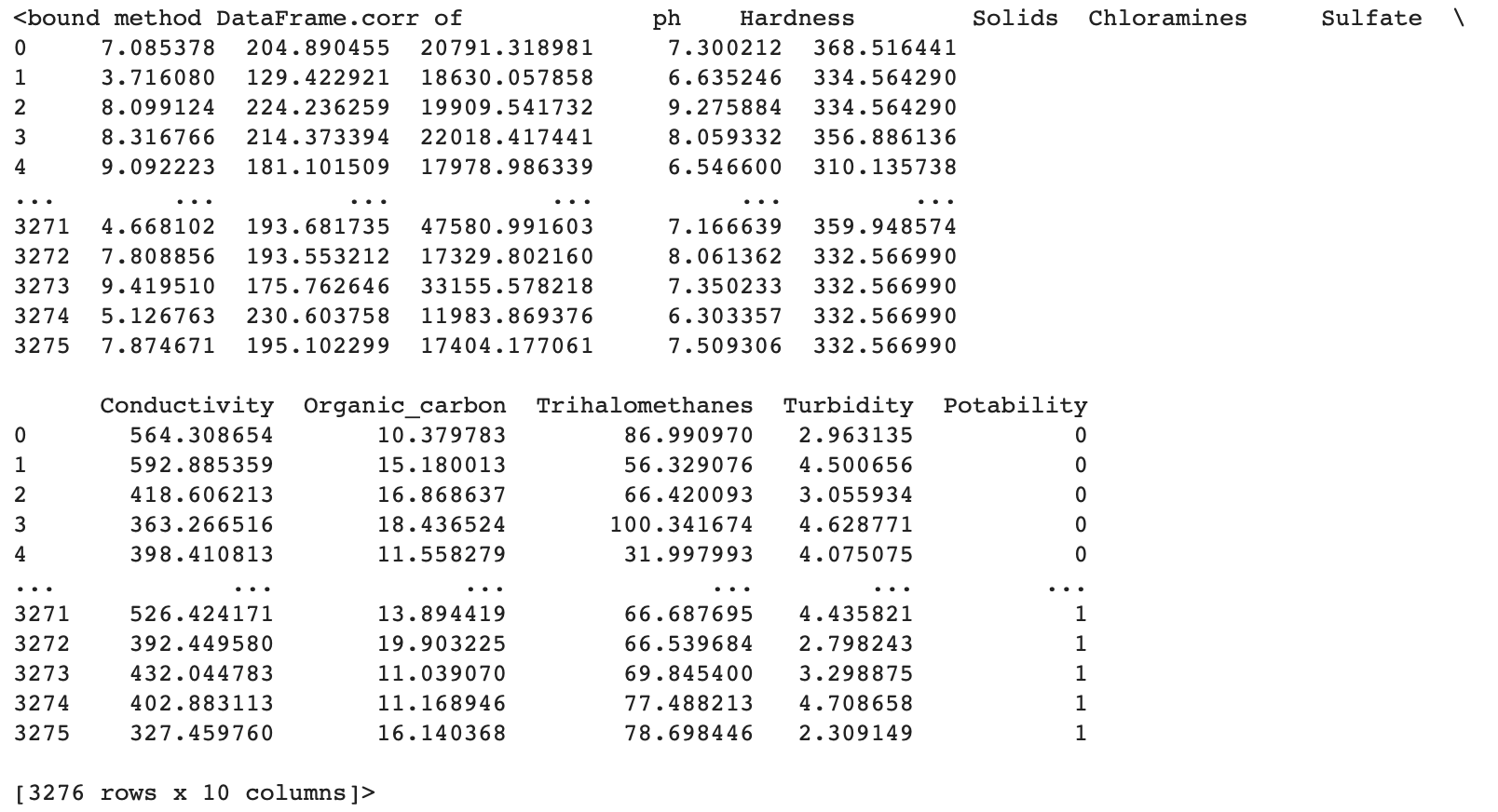
#How many missing values are there in the dataset?

df.isna().sum()

ph                 491
Hardness             0
Solids               0
Chloramines          0
Sulfate            781
Conductivity         0
Organic_carbon       0
Trihalomethanes    162
Turbidity            0
Potability           0
dtype: int64

From the result above, the rows missing data are ph- missing 491 values, Sulfate - missing 781 values, and Trihalomethanes - missing 162 values.
I will be using the mean of the each of the features that contains missing values to populate the column.

#Replace NaN values based on the group sample mean
df['ph']=df['ph'].fillna(df.groupby(['Potability'])['ph'].transform('mean'))
df['Sulfate']=df['Sulfate'].fillna(df.groupby(['Potability'])['Sulfate'].transform('mean'))
df['Trihalomethanes']=df['Trihalomethanes'].fillna(df.groupby(['Potability'])['Trihalomethanes'].transform('mean'))

#Check if there are still missing values

df.isna().sum()

ph                 0
Hardness           0
Solids             0
Chloramines        0
Sulfate            0
Conductivity       0
Organic_carbon     0
Trihalomethanes    0
Turbidity          0
Potability         0
dtype: int64
All missing values have been populated.


The information about the dataset (mean, std, min,max, Q1,Q2,Q3)
df.describe()

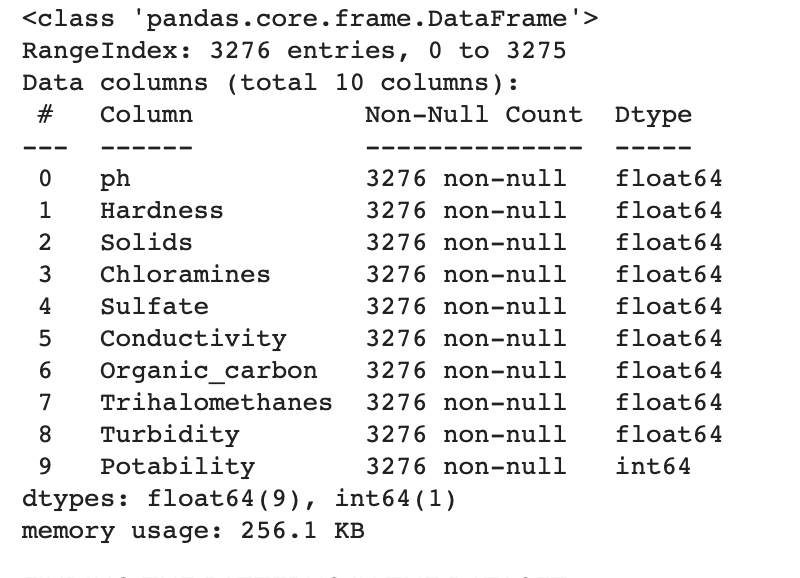
#Information about the dataframe
df.info()

FINDING THE PATTERNS IN THE DATASET

How the Independent variables relates to the Dependent variable

# Comparing one feature to the potabilty feature.
pd.crosstab(df.Potability, df.Sulfate

#Comparing two features to the potability feature.
pd.crosstab(df.Hardness [df.Potability==0], df.Sulfate [df.Potability==0])

# Checking for the hardness with data frame
df.hardness
0.      204.890455
1       129.422921
2       224.236259
3       214.373394
4       181.101509
           ...    
3271    193.681735
3272    193.553212
3273    175.762646
3274    230.603758
3275    195.102299
Name: Hardness, Length: 3276, dtype: float64

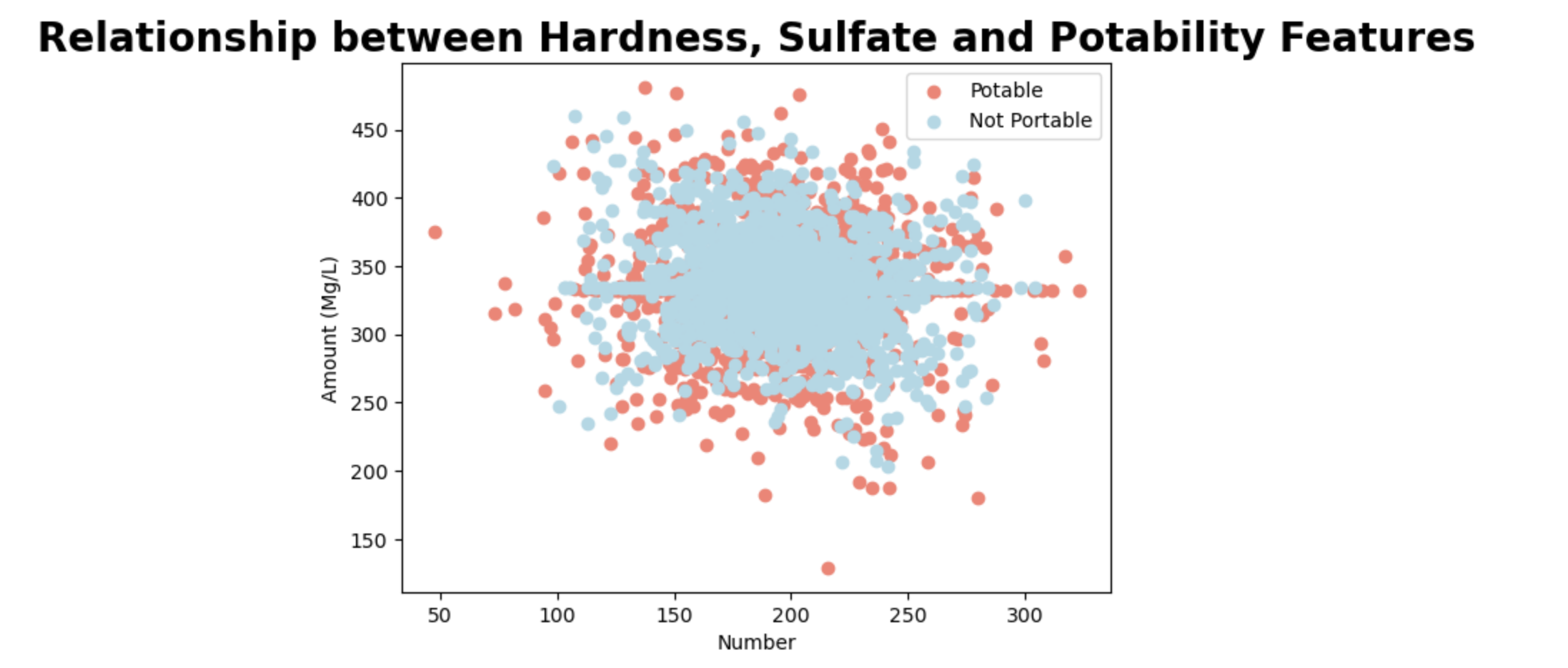
#Creating a Scattter Plot with results above where 1 = Potable, 0 = Not Potable

plt.scatter (df.Hardness [df.Potability==1], df.Sulfate [df.Potability==1], color="Salmon")

plt.scatter (df.Hardness [df.Potability==0], df.Sulfate [df.Potability==0], color="lightblue")

plt.title("Relationship between Hardness, Sulfate and Potability Features", size=20, weight='bold')

plt.legend (["Potable", "Not Portable", ""])

plt.xlabel("Number")

plt.ylabel("Amount (Mg/L)";

# Check the distribution of another feature ( Chloramines) with a histogram

df. Chloramines.plot.hist()
plt.ylabel("Amount (Mg/L)")
plt.title("Chloramines Feature", size=20, weight='bold')


![Screenshot 2024-11-27 at 11.27.45 AM.png](Screenshot%202024-11-27%20at%2011.27.45%E2%80%AFAM.png)

After finding patterns in the dataset, understanding how all the features relates to each other is derived through correlation matrix.

#Correlation function
df.corr

# Making Correlation more visual for better understanding

fig=plt.figure(figsize=(15,10))
sns.heatmap(df.corr(), annot=True, fmt='0.2f', square=True)
plt.title("Correlation Matrixs", size=20, weight='bold')

Text(0.5, 1.0, 'Correlation Matrixs')

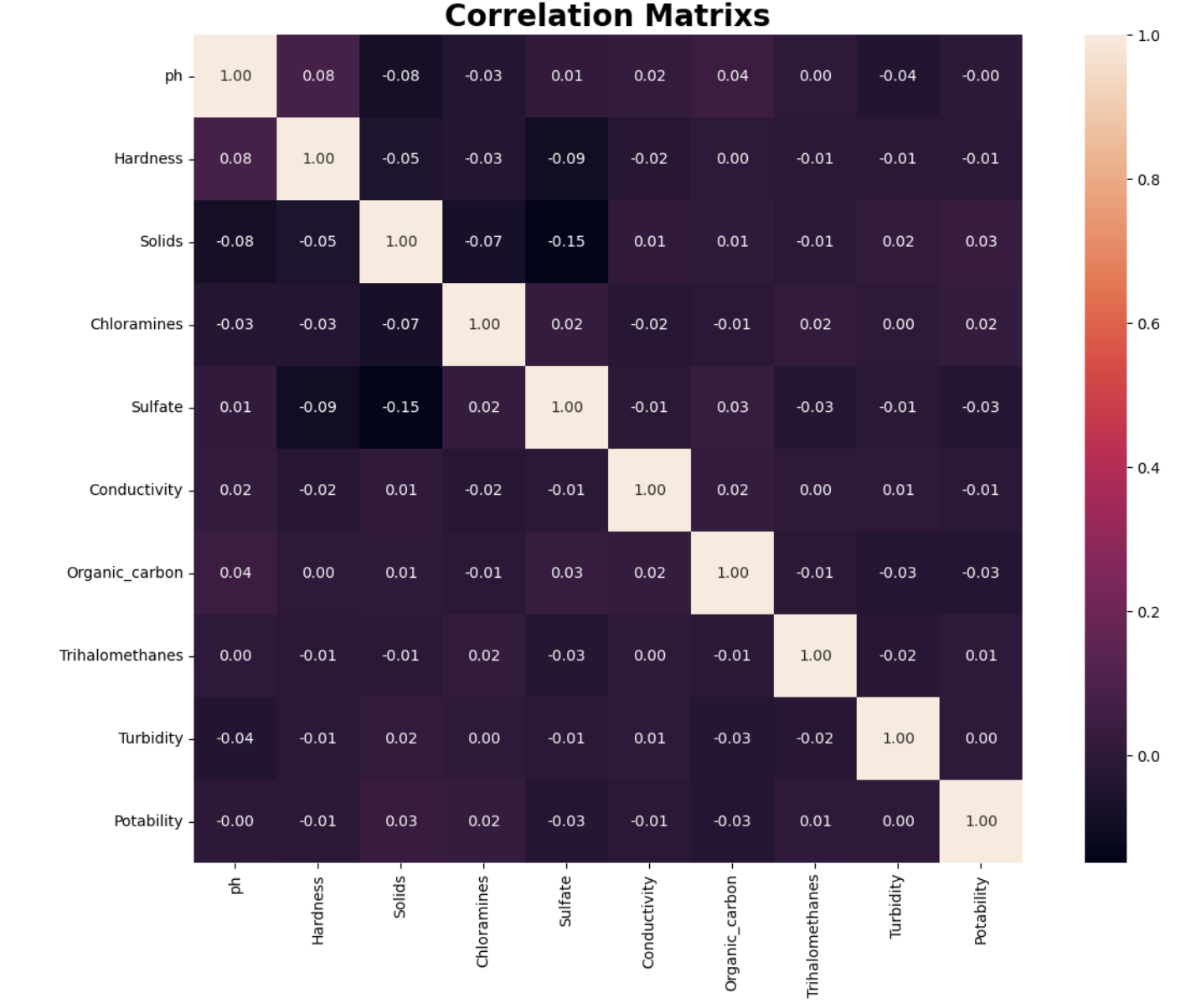
The 1.0 in the diagonal is given a perfect correlation which means the feature is equal from both x and y. This also shows how the Independent variables contributes to the dependent variable.

Preparing the Data for Machine Learning Modelling

Going back to the problem statement, which is, Can a machine learning model be created to predict water potabilty with at least a 95% accuracy?

#View all the top row data
df.head()

# Split Data into X and Y

X= df.drop("Potability", axis=1)
Y= df["Potability"]

#Let's see what X rows and columns looks like
X

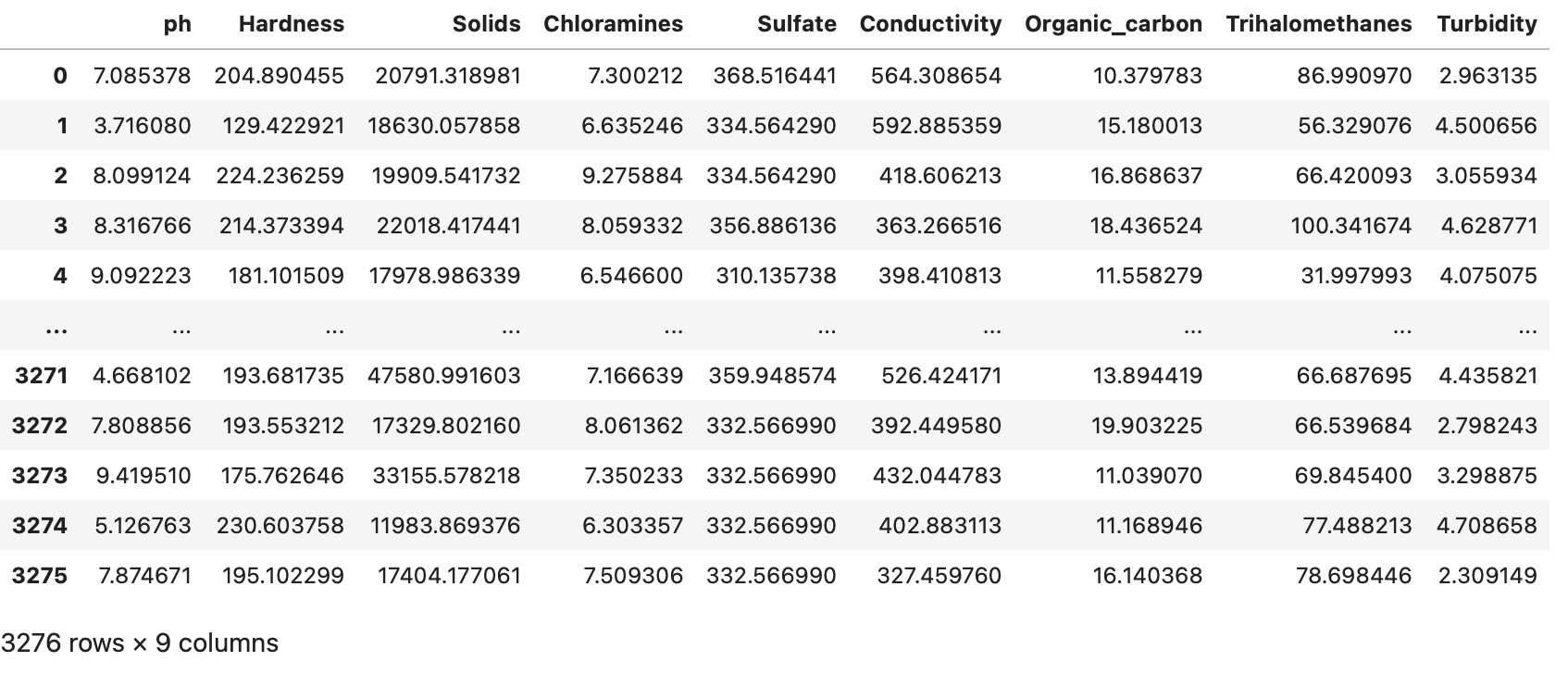
From the dataframe above, the Potability row is longer visible. and we have a length of 3,276 rows and 9 columns

#Let's see what Y row and column looks like

Y

From the above dataframe we have just 1 column (Potability) and a total length of 3276.

To create a good model, the dataset has to be spilt into test and train, simply because we want to be able to use the test data to see how well the model performs.

#Spilt data into train and test sets where 80% of the data is for training and 20% is for testing
np.random.seed(42)

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.20)

#Get the length of both X train and Y train
X_train, len(Y_train)

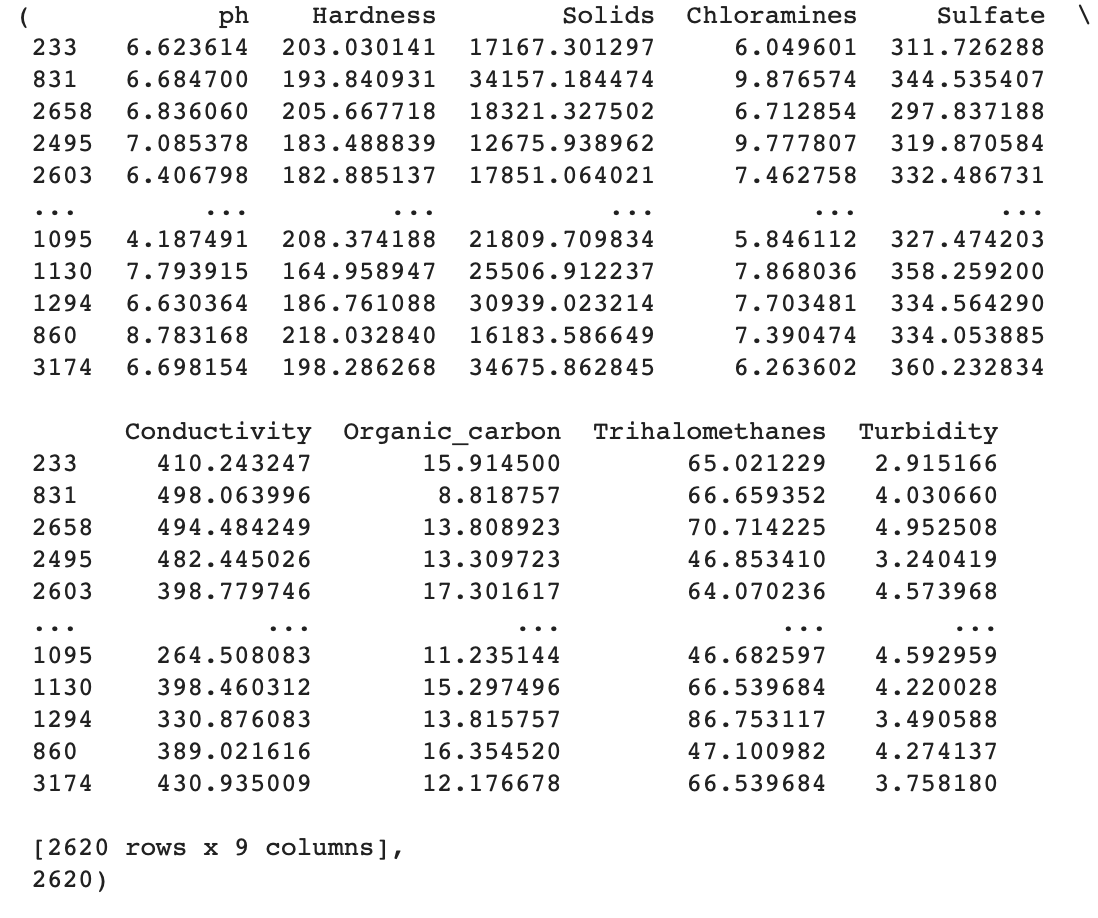
From the dataframe above we can see that there is 2620 rows with 9 Columns which is equal to 80% of the total dataset.

#Get length of the X test and Y test

X_test, len(Y_test)

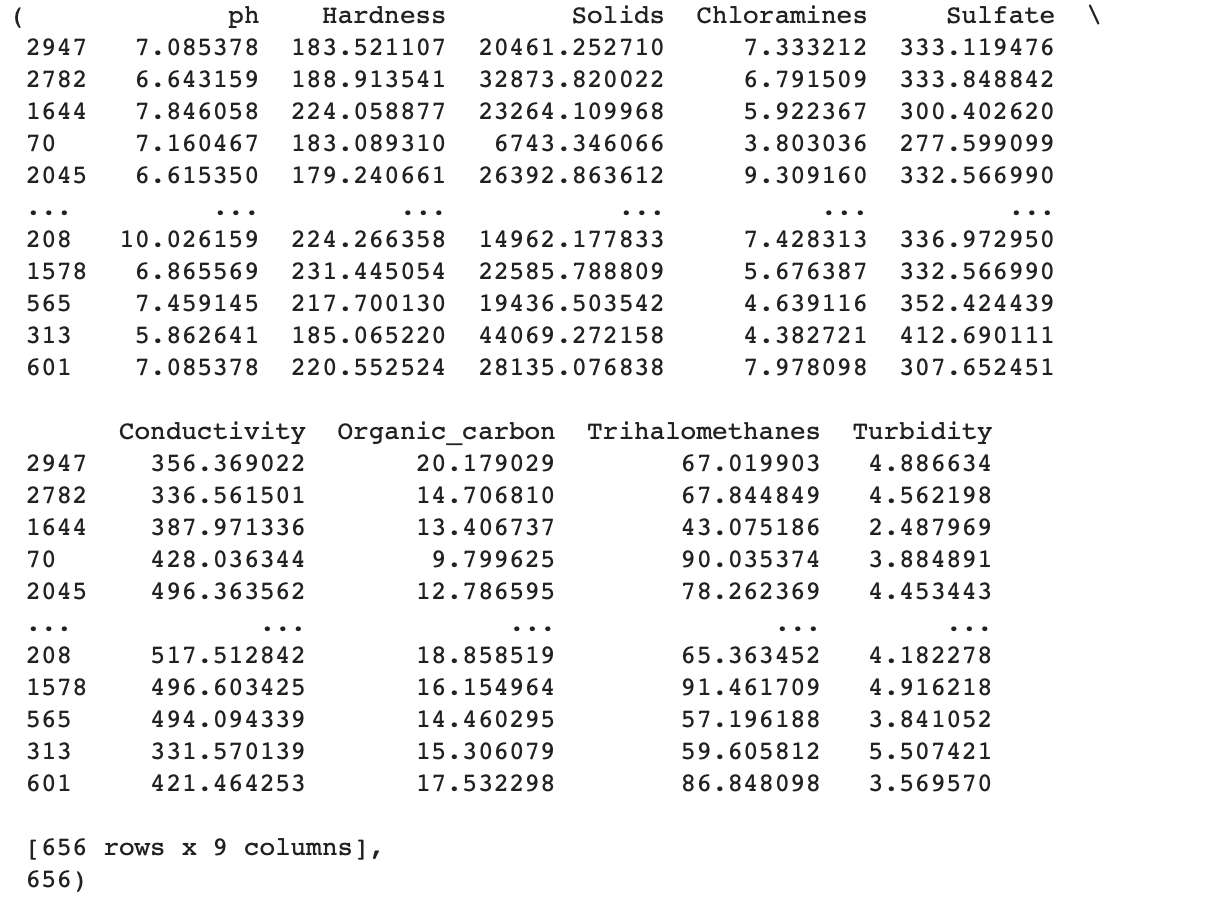
From the above dataframe we can see that there is a total of 656 rows with 9 columns which is equal to 20% of the dataset

From the Exploratory Data Analysis (EDA), there was a total of 3275, after spiltting the dataset into train and test. There is a total of 2620 for the training set.

The training dataset will be used to find patterns and the test set will be used to test the model created.

To find a suitable model for this project, Three different machine learning models will be used to determine the model with a good accuracy that meets the problem statement requirement which is at least a 95% accuracy.

The machine learning models are as follows:

K-Nearest Neighbor
Random Forest Classifier
Logistic Regression
Now, we have fit the training dataset with all three models, let's see accuracy result for each of the model.

#Model Dictionary

models = {"Logistic Regression": LogisticRegression(),
          "KNN":KNeighborsClassifier(),
          "Random Forest": RandomForestClassifier()}

models
{'Logistic Regression': LogisticRegression(),
 'KNN': KNeighborsClassifier(),
 'Random Forest': RandomForestClassifier()}

#Creating a function called potability_fit_score
def potability_fit_score(models, X_train, X_test, Y_train, Y_test):
    
    """
 fits and evaluates given machine learning models.

 Models: A dict of different Scikit-learn machine learning models.

 X_train: Training data (with training labels)

 X_test: Testing data (No labels)

 Y_train: Training data (with training labels)

 Y_test: Testing data (No labels)

 """
    np.random.seed(42) #set randon seed
    
    modelfit_scores = {}
    
    #Loop through the models
    #fit the model to train data
    #Evaluate the model and append the score to the model_scores
    
    for name, model in models.items():
        model.fit(X_train, Y_train)
        model_scores[name]=model.score(X_train, Y_train)
    return  model_scores

model_RandomForest = RandomForestClassifier()
model_RandomForest.fit(X_train, Y_train)

model_RandomForest.score(X_train, Y_train)
1.0

From the above result there is a 100% accuracy when the training dataset was used for Random Forest Machine Learning Model

The next model I am going to use is the K Nearest Neighbour

The next model I am going to use is the K Neighbour

model_KNN =KNeighborsClassifier()

model_KNN.fit(X_train, Y_train)
model_KNN.

0.7145038167

#From the above result, there is a 71% accuracy when the training dataset was used for the KNearest Neighbor Machine Learning model

The final model i will be using is the Logistic Regression Model.

model_LogisticRegression = LogisticRegression()
model_LogisticRegression.fit(X_train, Y_train)
model_LogisticRegression.score(X_train, Y_train)

0.6061068702290077

From the above result, there is a 60% accuracy when the training dataset was used for the KNearest Neighbor Machine Learning model

Lets look at the model results in a bar chart

fig, ax =plt.subplots()


models =['','LogisticRegression', 'KNN', 'RandomForest']


models_labels =['','red','blue', 'green']


models_result = ['','0.60', '0.71', '1.0']


bar_colors= ['tab:red','tab:blue', 'tab:green']


ax.bar(models, models_result, label=models_labels, color=bar_colors)

ax.set_ylabel("Number")
ax.set_xlabel("Model Name")
ax.set_title("Model Comparison", size=20, weight='bold')
ax.legend(['Random Forest','Logistic Regression','KNN',])

plt.show()

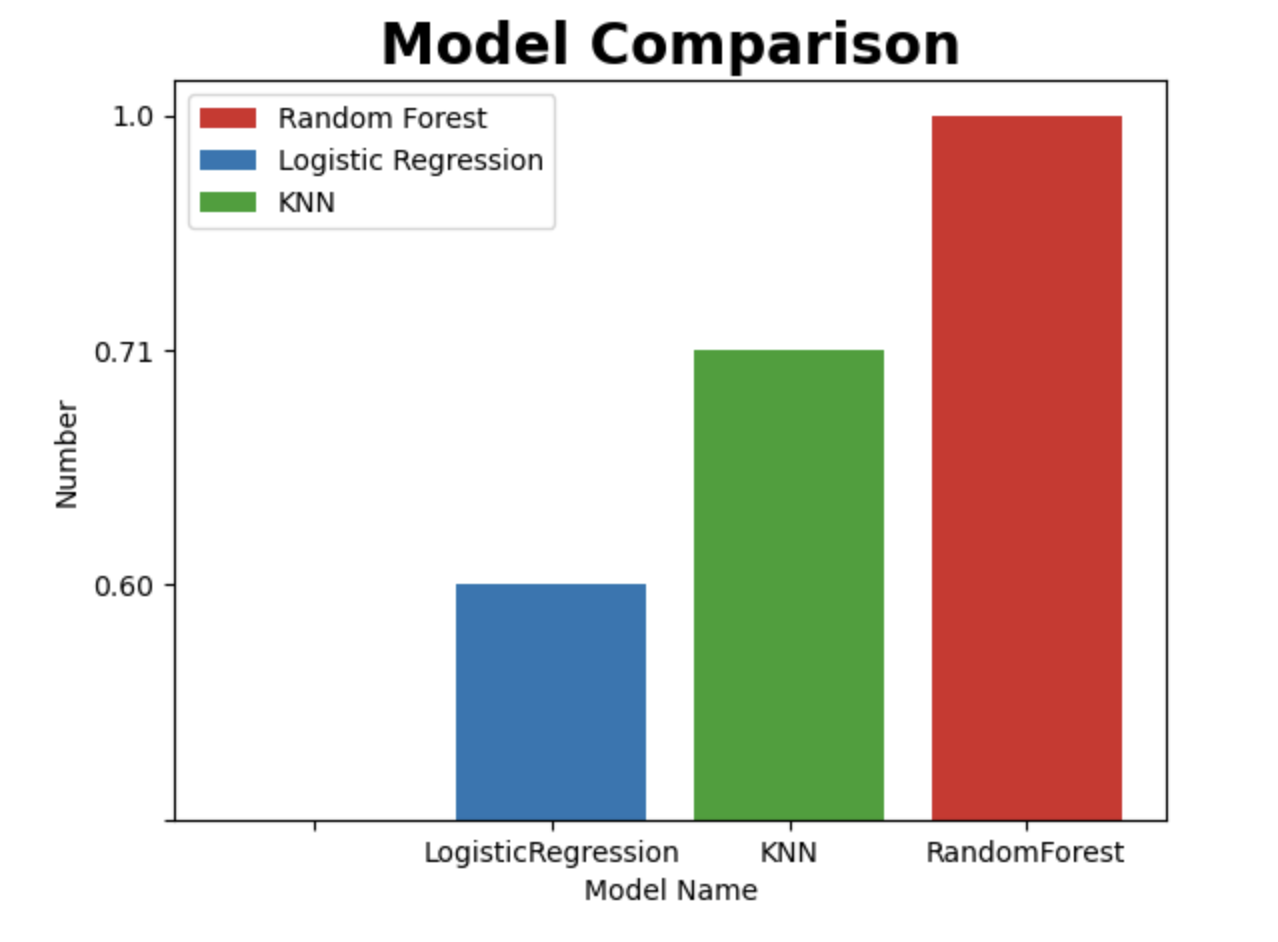
From the visualisation Bar Chart, we can see that Random Forest has a high accuracy for the prediction of the water quality and potability.

TUNING AND IMPROVING THE MODELS

After getting the baseline for the models, Hyperparameters can be tuned to improve the models, Feature importance, confusion matrix, Cross-validation, Precision, recall, F1 score, Classification report Roc curve, Area under curve (AUC)

# Tuning and Improving the baseline score

train_scores=[]
test_scores=[]


#Create a list of different values for the n-neighbors
neighbors=range(1,21)


#setup the KNN instance
knn= KNeighborsClassifier()


#Loop through different K-neighbors
for i in neighbors:
    knn.set_params(n_neighbors=i)
    knn.fit(X_train, Y_train)
    train_scores.append(knn.score(X_train,Y_train))
    test_scores.append(knn.score(X_test, Y_test))

knn.fit(X_train, Y_train)
knn.score(X_train, Y_train)
0.6339694656488549

From the hyperparameter tuning, the accuracy for K Nearest Neighbor Machine learning model is 60% and still does not meet the problem statement requirement.

Let's compare how KNearest Neighbor did before Hyper Tuning and after Hyper Tuning

# Visualise the Knearest Neighbor model before and after hyperparameter tuning
plt.plot(neighbors, train_scores, label="Train Score")
plt.plot(neighbors, test_scores, label="Test Score")
plt.xlabel ("Number of neighbors")
plt.xlabel("model Score")
plt.title("Train and Test Score", size=20, weight='bold')
plt.legend()
plt.ylabel("Model Accuracy")
print (f"Maximum KNN score on the test data: {max(test_scores)*100:2f} %")

Maximum KNN score on the test data: 61.432927 %

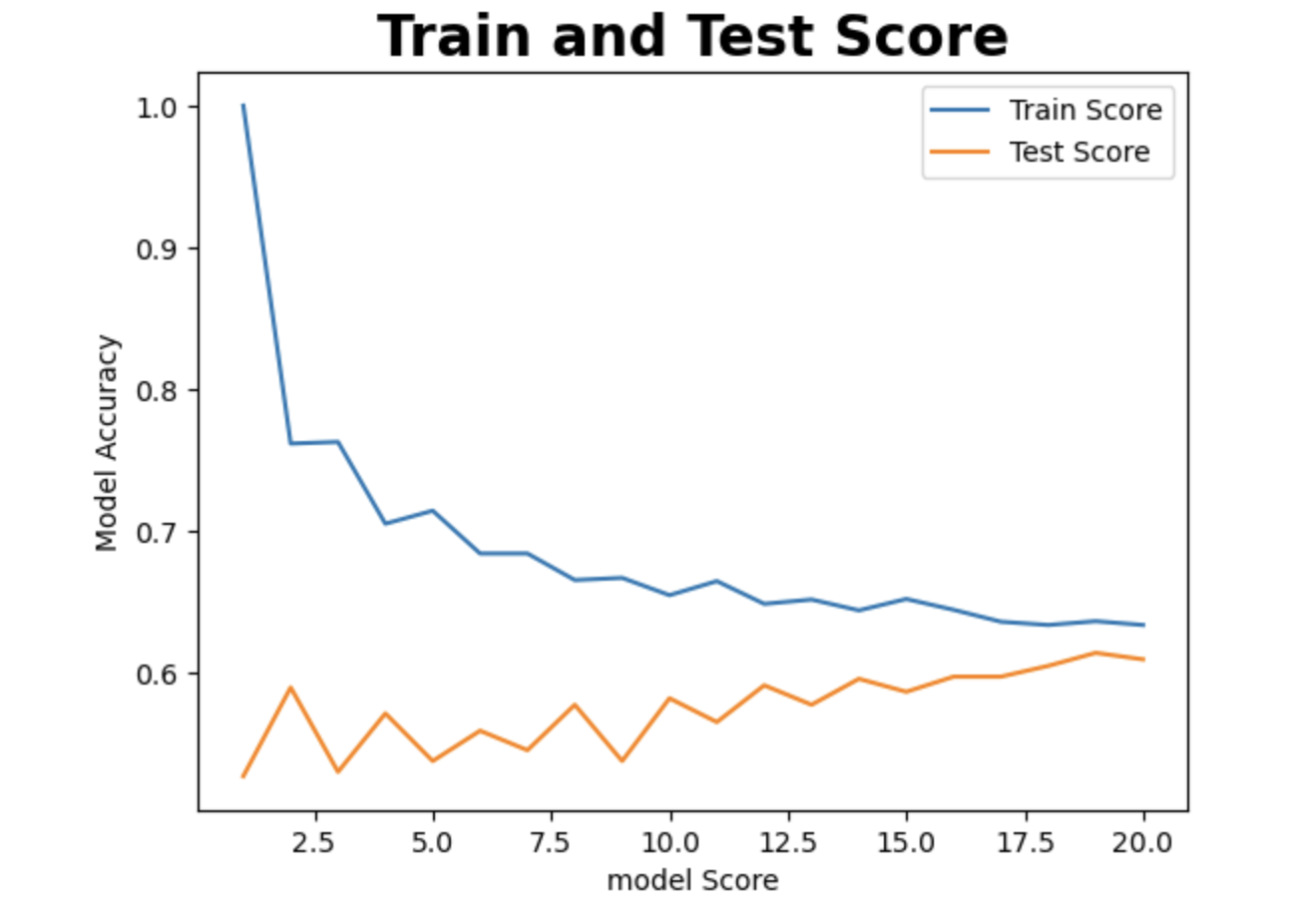
From the graph shown above, The Knearest Neighbor did better in the training dataset that it did with the test dataset.

Tuning the following models using Randomized Search CV:

Logistic Regression()

# Creating a Parameter Grid for Logistics Regression
log_reg_grid= {"C": np.logspace(-4,4,20), "solver": ["liblinear"]}
np.logspace(-4,4,20)

array([1.00000000e-04, 2.63665090e-04, 6.95192796e-04, 1.83298071e-03,
       4.83293024e-03, 1.27427499e-02, 3.35981829e-02, 8.85866790e-02,
       2.33572147e-01, 6.15848211e-01, 1.62377674e+00, 4.28133240e+00,
       1.12883789e+01, 2.97635144e+01, 7.84759970e+01, 2.06913808e+02
       5..45559478e+02, 1.43844989e+03, 3.79269019e+03, 1.00000000e+04])

After setting up the hyper parameters grids, I am going to tune them using the Randomised Search CV

Tune Logistic Regression
np.random.seed(42)

#Setup random hyperparameter search for logistic Regression
rs_log_reg=RandomizedSearchCV (LogisticRegression(), param_distributions=log_reg_grid, cv=5,n_iter=20, verbose=True)


#fit randomized search hyperparameter for Logistic Regression Model for train datasets
rs_log_reg.fit(X_train,Y_train)
rs_log_reg.best_params_

Fitting 5 folds for each of 20 candidates, totalling 100 fits
{'solver': 'liblinear', 'C': 0.0006951927961775605}

fit randomized search hyperparameter for Logistic Regression for scoring the test datasets

rs_log_reg.score (X_test,Y_test)
0.6280487804878049

After tuning using the Randomized Search CV we still get a 62% accuracy for Logistic Regression

Tuning the Logistic Regression Hyperparameter model using GridSearchCV

# Different Parameters for logistic regression model

log_reg_grid= {"C": np.logspace (-4, 4, 30), "solver": ["liblinear"]}


#setting up grid hyperparameter search for Logistic Regression
gs_log_reg = GridSearchCV (LogisticRegression(), param_grid=log_reg_grid, cv=5, verbose=True)


#Fit grid hyperparameter
gs_log_reg.fit(X_train, Y_train)

Fitting 5 folds for each of 30 candidates, totalling of 150 fits


GridSearchCV(cv=5, estimator=LogisticRegression(),
             param_grid={'C': array([1.00000000e-04, 1.88739182e-04, 3.56224789e-04, 6.72335754e-04,
       1.26896100e-03, 2.39502662e-03, 4.52035366e-03, 8.53167852e-03,
       1.61026203e-02, 3.03919538e-02, 5.73615251e-02, 1.08263673e-01,
       2.04335972e-01, 3.85662042e-01, 7.27895384e-01, 1.37382380e+00,
       2.59294380e+00, 4.89390092e+00, 9.23670857e+00, 1.74332882e+01,
       3.29034456e+01, 6.21016942e+01, 1.17210230e+02, 2.21221629e+02,
       4.17531894e+02, 7.88046282e+02, 1.48735211e+03, 2.80721620e+03,
       5.29831691e+03, 1.00000000e+04]),
                         'solver': ['liblinear']},
             verbose=True)

#check for the best hyperparameters
gs_log_reg.best_params_

{'C': 0.0006723357536499335, 'solver':

#Evaluate the grid search cv 

gs_log_reg.score(X_test, Y_test)

0.6280487804878049

When RandomizedSearchCV was used to tune the hyperparameters we derived a 62% accuracy Also, after tuning with GrisSearchCV a 62% accuracy

After Hyper Tuning the other model parameters i still did not meet the criteria for the problem statement and ince a 100% accuracy was acheived with Random Forest Classification. I will be evaluating the model for the following:

1.Accuracy 2.ROC Curve 3.Confusion Matrix 4.Classification matrix 5.Precision 6. Recall 7.F1_Score 8.Cross-validation

# To evaluate the Random Forest Classifier model, I will utilize the test data for prediction

model_RandomForest.fit(X_test, Y_test)
RandomForestClassifier()
y_preds=model_model_RandomForest.predict(X_test)

array([0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0,
       0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0,
       0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0,
       1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1,
       0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0,
       0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1,
       0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0,
       1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1,
       0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1,
       0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0,
       0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0,
       0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1,
       1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1,
       1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1,
       1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
       0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1,
       0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0,
       0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0,
       0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1,
       0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1,
       0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1,
       0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0,
       0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0,
       0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0,
       0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0,
       0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1,
       1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1,
       0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1,
       0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0,
       1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0], dtype=int64)

#The array of numbers above shows the prediction of water potability using the test data where 1 represents 1 safe for consumption and 0 represents not potable.

Y_test

2947    0
2782    1
1644    0
70      0
2045    1
       ..
208     0
1578    1
565     0
313     1
601     0
Name: Potability, Length: 656, dtype: in

The Test dataset that had 9 columns (X_Test) was used to predict the Potabilty column (Y_Test) as shown above

Computing a confusion matrix anatomy to know how well the model performed in predicting.
print (confusion_matrix (Y_test, y_preds))

[[412   0]
 [  0, 244]]

From the confusion matrix we can see that the Y_test data had 412 values that was = 0, but after using the model to predict we got a total of 244 values = 0

#Plot confusion matrix  using a function

def plot_conf_mat(Y_test,Y_preds):
    
 """"
 Plots a nice looking confusion matrix using a seaborn's heatmap()
 
 """
fig, ax = plt.subplots(figsize=(3,3))
ax=sns.heatmap (confusion_matrix(Y_test, y_preds), annot=True, cbar=False)
plt.xlabel("True label")
plt.ylabel("Predicted label")
bottom, top = ax.get_ylim()
ax.set_ylim(bottom +0.5, top -0.5)
plot_conf_mat(Y_test, y_preds)

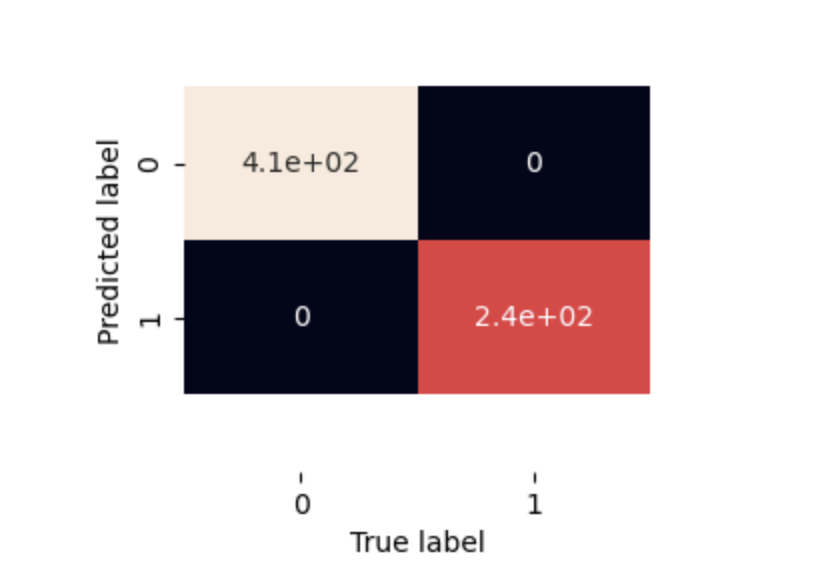
Confusion Matrix Analogy

True positive = model predicts 1 when the Truth is 1

False positive = model predicts 1 when the Truth is 0

True Negative = model predicts 0 when truth is 1

False Negative= model predicts 0 when the truth is 1

After the confusion matrix analogy, I want to also get a classification report as well as a cross validated precision, recall and f1-score.

#Classification report

print(classification_report(Y_test, y_preds)

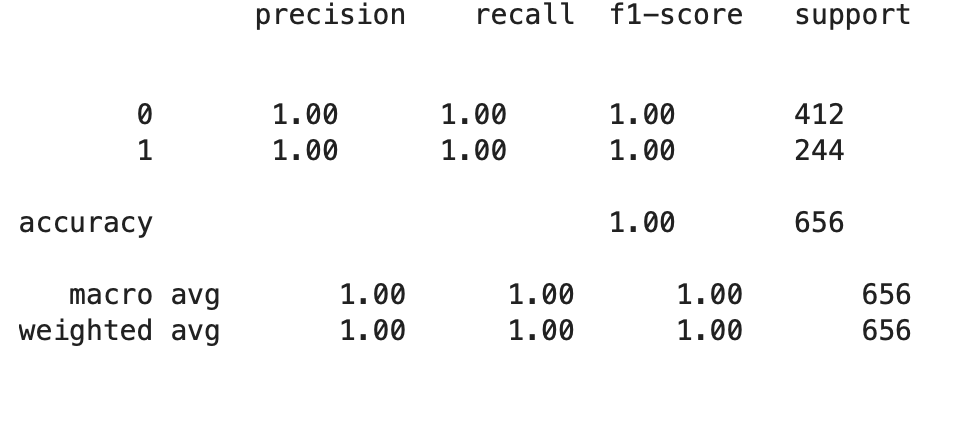
What the classification report represents is:

Precision: No false positive

Recalls: Proportion of actual positive

f1-score: This is a combination of precision and recall

Support: Which shows the number of samples the report used to calculate.

Finding the highest and least features that contributed to the predictions.

# Displaying X_test data

#Save X_test into a css
df_X_test=pd.DataFrame (X_test)
df_X_test

#This will save the X_test to a csv file.

df_X_test. to_csv ("X_test")

#Creates the feature importance between the Test dataset features.
feature_importance=df_X_test.corr()
feature_importance

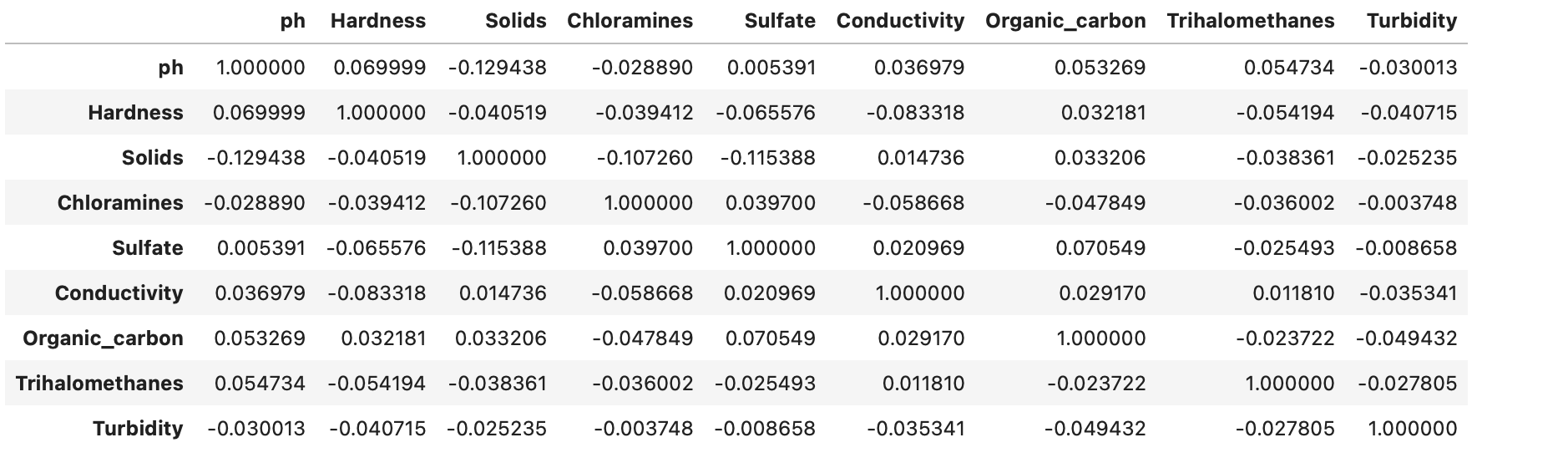
#Creating a dictionary for the features and values.

dict= {"ph":1.000000,
       "Hardness":0.069999,
        "Solids":-0.129438,
        "Chloramines":-0.028890,
        "Sulfate":0.005391,
         "Conductivity":0.005391,
         "Organic_carbon":0.053269,
          "Trihalomethanes":0.054734,
           "Turbidity":-0.030013};

dict

{'ph': 1.0,
 'Hardness': 0.069999,
 'Solids': -0.129438,
 'Chloramines': -0.02889,
 'Sulfate': 0.005391,
 'Conductivity': 0.005391,
 'Organic_carbon': 0.053269,
 'Trihalomethanes': 0.054734,
 'Turbidity': -0.30013}

#visualising the feature importance
features_df = pd.DataFrame(dict, index=[0])
features_df.T.plot.barh(title="Feature Importance", color="orange", legend=False, ylabel="Features", xlabel="Importance Number");

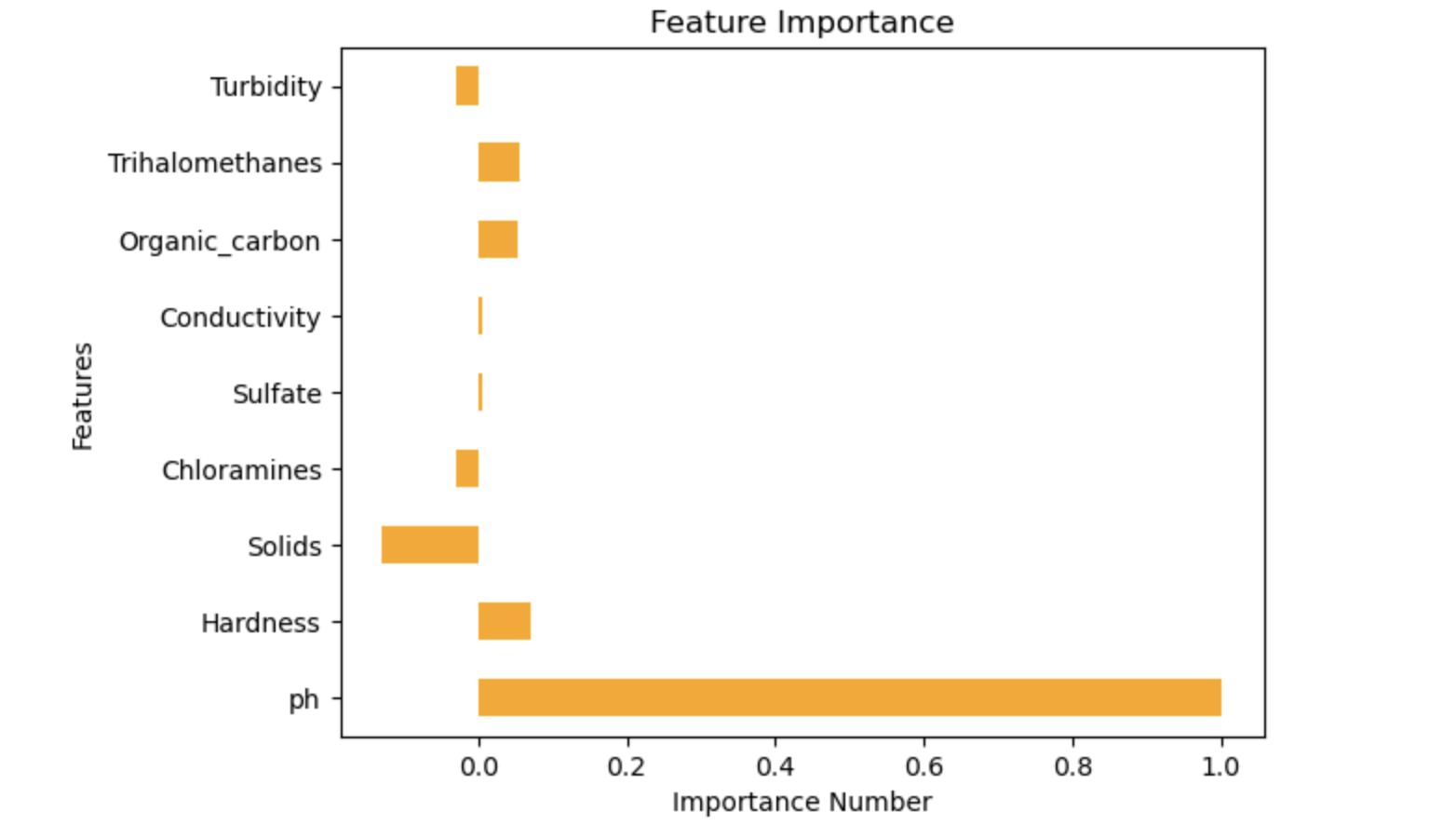
From the above visualisation we can see that the most important feature that contributed to the prediction for the water consumption was ph.

Also, the least feature that contributed to the prediction of the dataset was Sulfate and Conductivity.

Going back to our problem statement which was:

I wanted to find out Information about the features or factors contributing to the quality of water and from the visualising above Ph, Hardness, Organic carbon, Trihalomethanes all contribute to the quality of water.
With Ph having a high contributing factor of 1.0.

From the data prediction,the knowledge of the results derived can help reduce risk in terms of spread of harmful bacterias and diseases.

I have been able to get more inisght into the water quality potability dataset by exploring the patterns.

DISCLAIMER

All Derived Results from this machine learning model was derived based on the Water Potability Dataset gotten from Kaggle.