### TL;DR The paper introduces the SVR-Tree algorithm, a method for handling imbalanced data in classification trees by penalizing the Surface-to-Volume Ratio (SVR) of decision boundaries. This approach aims to regularize decision boundaries to prevent overfitting, especially in scenarios with limited data in one class. The method is theoretically robust, offering consistency and good convergence rates, but its effectiveness depends on specific assumptions about data regularity and computational feasibility. The SVR-Tree compares favorably with other methods like SMOTE, though it may face challenges in high-dimensional or highly complex datasets.--DIVIDER--### Introduction Classification is a corner stone of Machine Learning, but the problem becomes more complex when we have to handle imbalnced Classification, There is not any fixed definition for exact imbalanced defintion, however imbalanced ration is one of the metric for imbalanced classification, but there is not stadard threshold, above which data is called imbalanced, In short we can say highly disproportionate class distribution is imbalnace ### Perspective Research: Reviewing Articles with Diverse Viewpoints on Imbalanced Data in Classification To provide a broader context to the discussion on imbalanced data in classification trees and the SVR-Tree approach presented in the paper, I will review diverse perspectives from other articles on this topic. This will help to understand how the SVR-Tree method compares and contrasts with other approaches in the field. #### 1. **"A Comprehensive Review on Handling Imbalanced Data in Classification" by Haixiang Guo et al. (2017)** - **Perspective:** This review paper discusses a wide range of techniques for dealing with imbalanced data, including data-level approaches like oversampling and undersampling, algorithm-level approaches such as cost-sensitive learning, and hybrid approaches that combine both strategies. - **Comparison:** While the SVR-Tree algorithm focuses on regularizing the decision boundary shape, this review highlights that other methods, particularly hybrid approaches, may address imbalanced data by simultaneously altering the training data distribution and modifying the learning algorithm. The review suggests that no single method is universally best, and the choice depends on the specific characteristics of the dataset. - **Relevance:** This paper’s discussion on the limitations of oversampling (e.g., risk of overfitting) aligns with the motivation behind SVR-Tree’s regularization approach, which aims to mitigate overfitting by smoothing decision boundaries. #### 2. **"SMOTE: Synthetic Minority Over-sampling Technique" by Nitesh V. Chawla et al. (2002)** - **Perspective:** SMOTE is a widely recognized technique that generates synthetic samples for the minority class to address class imbalance. The paper presents SMOTE as a method to create larger, less specific decision regions, thereby reducing overfitting in minority classes. - **Comparison:** SMOTE aims to expand the decision regions, which contrasts with the SVR-Tree's approach of constraining decision boundaries through regularization. While SMOTE is effective in many scenarios, the SVR-Tree offers an alternative by focusing on the geometric properties of the decision boundary rather than data augmentation. - **Relevance:** The discussion on SMOTE’s efficacy in various scenarios underscores the importance of considering decision boundary shapes, which the SVR-Tree method directly addresses. #### 3. **"A Survey of Machine Learning Techniques for Handling Imbalanced Data" by H. He and E.A. Garcia (2009)** - **Perspective:** This survey categorizes techniques for handling imbalanced data into preprocessing methods (like oversampling and undersampling), algorithmic modifications, and ensemble methods. It emphasizes the trade-offs between these methods, such as complexity versus effectiveness. - **Comparison:** The SVR-Tree’s emphasis on algorithmic modification (via regularization) fits into the broader category of algorithm-level solutions discussed in this survey. The paper suggests that while preprocessing methods are simpler, algorithmic modifications can offer more robust solutions in specific contexts, which is the niche the SVR-Tree aims to fill. - **Relevance:** The survey’s insights into the trade-offs between different methods highlight the potential advantages of the SVR-Tree’s approach in scenarios where preserving the decision boundary’s regularity is critical. #### 4. **"Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning" by Han et al. (2005)** - **Perspective:** Borderline-SMOTE is an extension of SMOTE that focuses on generating synthetic samples for instances near the decision boundary, aiming to improve the classifier's ability to distinguish between classes. - **Comparison:** Borderline-SMOTE and SVR-Tree both pay attention to the decision boundary but from different angles. Borderline-SMOTE enhances the boundary’s resolution by focusing on difficult instances, while SVR-Tree regularizes the boundary’s shape to avoid overfitting. Both methods recognize the importance of the decision boundary but apply different strategies to improve classification performance. - **Relevance:** The approach taken by Borderline-SMOTE reflects the importance of decision boundary management in classification, a concept that is central to the SVR-Tree method as well. #### 5. **"Cost-Sensitive Learning and the Class Imbalance Problem: A Review" by X. Zhou and X. Liu (2006)** - **Perspective:** This paper reviews cost-sensitive learning techniques that adjust the learning process based on the costs associated with misclassifying different classes, particularly in imbalanced datasets. - **Comparison:** Cost-sensitive learning is an alternative to data-level or algorithm-level approaches, where the learning algorithm is adjusted to penalize misclassifications of the minority class more heavily. While SVR-Tree does not explicitly use cost-sensitive techniques, its regularization approach could be seen as implicitly reducing the cost of overfitting to the minority class by smoothing the decision boundaries. - **Relevance:** The cost-sensitive learning perspective complements the SVR-Tree’s focus on decision boundary regularization, providing another angle on how to handle the imbalanced data problem. The articles reviewed provide a comprehensive view of the various methods available to tackle imbalanced data in classification problems. The SVR-Tree method offers a novel algorithmic approach by focusing on the regularization of decision boundaries, which contrasts with the more common strategies of data augmentation and cost-sensitive learning. Each method has its strengths and weaknesses, and the choice of technique depends on the specific characteristics of the dataset and the goals of the analysis. The diverse perspectives highlight that while SVR-Tree provides strong theoretical guarantees, it should be considered alongside other methods like SMOTE, ADASYN, and cost-sensitive learning, depending on the application scenario. --DIVIDER--## Methodology The SVRTree is different from CART (Classification and Regression Tree) in two ways, first of all cart assigns the leaf prediction according to the proportion of the leaf node, however in case of SVR Tree the prediction is independent of the proportion of classes in the leaf, and a signed impurity, and other is regularization of tree to minimize surface to volumne ratio. ### Signed Impurity: Mathematical Expression and Definition In the context of the SVR-Tree methodology, the **signed impurity** is used to measure the quality of a classification tree's decision rule, taking into account both the purity of the nodes (how well the nodes separate the classes) and whether the predicted class for a node matches the majority class in that node. #### Mathematical Expression for Signed Impurity Let $ T $ be a classification tree with leaf nodes $ A_1, A_2, \dots, A_m $, where each node $ A_j $ is associated with a predicted class label $ z_j \in \{0, 1\} $ and a dominant class label $ \tilde{z}_j \in \{0, 1\} $ under the weighted probability measure $ P $. The **signed impurity** for a leaf node $ A_j $ under measure $ P $ is defined as: $$ \tilde{I}(A_j, P) = \begin{cases} I(A_j, P) & \text{if } z_j = \tilde{z}_j, \\ 1 - I(A_j, P) & \text{if } z_j \neq \tilde{z}_j, \end{cases} $$ where $ I(A_j, P) $ is the impurity of node $ A_j $, typically measured by a function such as Gini impurity or entropy. #### Explanation of Terms - **$ z_j $**: The predicted class label for node $ A_j $ based on the classification tree's decision rule. - **$ \tilde{z}_j $**: The dominant class label in node $ A_j $, i.e., the class label that would minimize the impurity if chosen as the prediction for that node. - **$ I(A_j, P) $**: The impurity of node $ A_j $, a measure of how mixed the classes are within the node. Lower impurity indicates a node that is predominantly one class. #### Interpretation - **$z_j = \tilde{z}_j $**: If the predicted class label $ z_j $ matches the dominant class label $ \tilde{z}_j $, the signed impurity $ \tilde{I}(A_j, P) $ is simply the regular impurity $ I(A_j, P) \). - **$ z_j \neq \tilde{z}_j $** If the predicted class label $ z_j $ does not match the dominant class label $ \tilde{z}_j $, the signed impurity $ \tilde{I}(A_j, P) $ is penalized, and it becomes $ 1 - I(A_j, P) $, reflecting a higher impurity due to the misclassification. The signed impurity is thus a measure that not only accounts for the purity of the node but also introduces a penalty when the predicted class does not align with the majority class within the node. This makes it a more comprehensive measure of the quality of the decision rule applied by the classification tree. #### Signed Impurity of a Tree: Mathematical Expression The **signed impurity of a tree** aggregates the signed impurities of all its leaf nodes to provide an overall measure of the tree's quality, considering both the purity of each node and whether the predicted class labels match the dominant class labels.The **signed impurity of the tree** $ T $ under measure $ P $ is defined as: $$ \tilde{I}(T, P) = \sum_{j=1}^{m} P(X \in A_j) \tilde{I}(A_j, P) $$ where: - **$ \tilde{I}(A_j, P) $**: The signed impurity of leaf node $ A_j $ as defined earlier. - **$ P(X \in A_j) $**: The probability that a sample $ X $ falls within the leaf node $ A_j $, under the weighted probability measure $ P $. By summing the weighted signed impurities across all leaf nodes, the signed impurity of the tree provides an overall assessment of the tree’s performance, balancing the trade-off between classification accuracy and the potential penalty for misclassifications within nodes. This measure is used in the SVR-Tree methodology to evaluate and optimize the quality of the tree as part of the regularization process. ### Surface-to-Volume Ratio (SVR) of a Tree The Surface-to-Volume Ratio (SVR) of a tree $ T $ is a measure of the complexity of the decision boundary that the tree creates. It is defined as the ratio of the total surface area of the decision set (which corresponds to the boundary of the regions classified as belonging to a particular class) to the volume of the decision set (which corresponds to the size of these regions). Let $ \mathcal{X}_1 $ be the decision set for the minority class (or the class of interest) in the tree $ T $, where $ \mathcal{X}_1 = \{x \in \mathcal{X} : T(x) = 1\} $. The **Surface-to-Volume Ratio (SVR) of the tree** $ T $ is mathematically expressed as: $$ r(T) = \frac{S(\mathcal{X}_1)}{V(\mathcal{X}_1)} $$ where: - **$ S(\mathcal{X}_1) $**: The surface area (boundary) of the decision set $ \mathcal{X}_1 $. - **$ V(\mathcal{X}_1) $**: The volume of the decision set $ \mathcal{X}_1 $. ### Mathematical Expression of SVR-Tree $$ \hat{T}_n = \arg\min_{\tilde{T} \in \mathcal{T}} \left[ I(T, P_n) + \lambda_n r(T) \right] $$ The SVR-Tree aims to find a classification tree that not only has low impurity (i.e., classifies the training data accurately) but also has a simple, regular decision boundary, as measured by the Surface-to-Volume Ratio. The penalty parameter $ \lambda_n $ allows the algorithm to control the balance between accuracy and boundary complexity, which is particularly useful for handling imbalanced data where overfitting to the minority class is a common concern. By minimizing this objective function, the SVR-Tree algorithm seeks to produce a decision tree that generalizes well to new, unseen data by avoiding overly complex, irregular decision boundaries. --DIVIDER--### Contrast Analysis: Comparison of Perspectives on Handling Imbalanced Data in Classification Trees | **Aspect** | **SVR-Tree (Surface-to-Volume Regularization)** | **SMOTE (Synthetic Minority Over-sampling Technique)** | **ADASYN (Adaptive Synthetic Sampling)** | |-------------------------------------|----------------------------------------------------------------------|------------------------------------------------------------------------|------------------------------------------------------------------| | **Methodology** | Penalizes Surface-to-Volume Ratio (SVR) to regularize decision boundaries. | Creates synthetic samples for the minority class to balance the dataset. | Similar to SMOTE but focuses more on difficult-to-classify samples. | | **Focus** | Regularization of decision boundary shape to prevent overfitting in imbalanced data scenarios. | Enlarges decision regions for the minority class by generating synthetic samples. | Adaptive generation of synthetic samples, prioritizing difficult cases. | | **Advantages** | - Improved generalization by avoiding complex decision boundaries.
- Theoretical consistency and convergence guarantees. | - Effective in reducing overfitting by balancing the class distribution.
- Simple to implement and widely used. | - More focused on handling difficult examples in the minority class.
- Potentially better performance in highly imbalanced datasets. | | **Challenges/Limitations** | - May obscure important patterns if the regularization is too strong.
- Computationally intensive compared to some other methods. | - Synthetic samples may not always represent the underlying distribution well.
- May struggle with high-dimensional data. | - Similar challenges as SMOTE, with added complexity in selecting the appropriate parameters.
- Potential risk of overfitting on noisy or redundant features. | | **Theoretical Foundation** | Based on penalizing the complexity of decision boundaries through geometric measures. | Based on oversampling with the aim of expanding decision regions.
- Rooted in statistical learning theory but relies heavily on heuristics. | - Builds on the SMOTE concept, with an emphasis on adaptively focusing on challenging cases.
- Also heuristic-driven with limited theoretical grounding. | | **Application Scenarios** | Best suited for datasets where decision boundary complexity leads to overfitting, particularly in low to moderately high dimensions. | Works well in a variety of imbalanced datasets, particularly when the minority class is under-represented. | Particularly useful in highly imbalanced datasets or when there are specific difficult-to-classify samples. | | **Performance in High Dimensions** | - May face challenges as the Surface-to-Volume Ratio becomes less intuitive in high dimensions.
- Requires careful tuning of regularization parameters. | - Performance typically degrades as dimensionality increases due to curse of dimensionality.
- Synthetic samples may become less meaningful. | - Similar to SMOTE, with added complexity in focusing on difficult samples in high dimensions.
- Might require extensive tuning. | | **Practical Use and Flexibility** | - Can be complex to implement and tune, but offers strong theoretical guarantees.
- Suitable for scenarios where interpretability and boundary regularity are key. | - Easy to implement and understand.
- Flexible but may require trial and error to tune effectively. | - More flexible than SMOTE in targeting specific difficult cases, but at the cost of added complexity and parameter tuning. | ### Summary of Contrast The SVR-Tree method contrasts with SMOTE and ADASYN in its focus on regularizing the complexity of decision boundaries rather than generating new data points. While SVR-Tree offers strong theoretical foundations and is well-suited for scenarios where interpretability and avoidance of overfitting are key, it may be more computationally intensive and less intuitive in high-dimensional spaces. On the other hand, SMOTE and ADASYN are more heuristic-based and easier to implement but may struggle with high-dimensional data and the generation of meaningful synthetic samples. 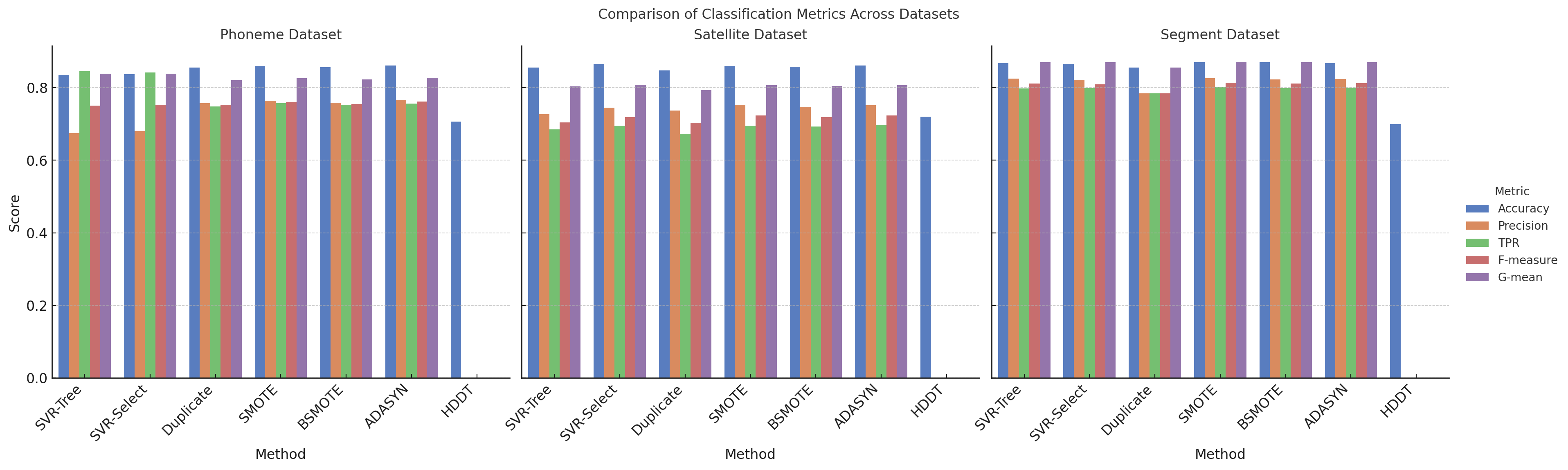This structured comparison highlights the strengths and weaknesses of each approach, helping to identify the most appropriate method depending on the specific characteristics of the dataset and the goals of the analysis.--DIVIDER--## Results ![output.png](output.png)--DIVIDER--### Conclusion The work presents a novel approach called SVR-Tree (Surface-to-Volume Ratio Tree) that effectively addresses the challenges associated with classification in the presence of imbalanced data. The key innovation of the SVR-Tree is the introduction of a regularization term based on the Surface-to-Volume Ratio (SVR) of the decision boundaries. This regularization penalizes overly complex and irregular decision boundaries, which are common when using traditional classification trees on imbalanced datasets. The theoretical analysis provided in the paper demonstrates that the SVR-Tree algorithm is consistent and converges at a good rate, making it a robust method for classification tasks. Experimental results across multiple datasets show that the SVR-Tree outperforms traditional methods, including CART with various oversampling techniques like SMOTE, Borderline-SMOTE, and ADASYN, particularly in terms of generalization performance and stability. Moreover, the SVR-Tree with feature selection further improves performance, indicating that combining SVR regularization with selective feature usage can lead to even more effective classification models. While the SVR-Tree shows strong promise, the paper acknowledges that the choice of the regularization parameter $\lambda_n$ is crucial and may require careful tuning depending on the specific dataset and application. In summary, the SVR-Tree offers a significant advancement in classification tree methodologies, particularly for imbalanced data scenarios. Its ability to maintain simpler, more regular decision boundaries while achieving high classification accuracy makes it a valuable tool for practitioners dealing with imbalanced datasets in various domains. Future work could explore further extensions of this method, including its application to multi-class problems and other types of classifiers.