![vagaro-xyxZWjuqeZA-tiny.png](vagaro-xyxZWjuqeZA-tiny.png) Credit: Photo by Vagaro on Unsplash # Abstract This case study explores an innovative subscription model introduced by a major financial institution in India to transform the traditional Point of Sale (POS) rental system. Merchants, who previously paid monthly rental fees for POS terminals, often faced difficulties maintaining sufficient account balances, leading to challenges in fee collection. To address this, the institution introduced a one-time subscription plan, eliminating recurring rental fees. Using the Kaplan-Meier estimator, the institution optimally priced the one-time fee based on merchant lifetime value (LTV), factoring in geography, merchant category, and turnover. This model enhances revenue predictability and mitigates risks associated with delayed or missed payments. Early results show strong market acceptance, with significant upfront revenue generated, and expansion plans are in progress. # Introduction Merchants are an integral part of a major financial institution’s business, and the bank offers a range of services to support their operations, including unified payment solutions such as Point of Sale (POS) terminals and payment gateways. Traditionally, merchants pay a monthly rental fee to retain their POS terminal IDs (TIDs). This fee is automatically deducted from the merchant’s linked Current Account (CA) through a standing instruction. However, in some cases, merchants struggle to maintain sufficient balances in their accounts, leading to difficulties in collecting charges like rental fees, low usage charges, and late settlement fees. Over time, these outstanding charges can accumulate, resulting in significant revenue losses for the bank. To address these challenges, the bank introduced a new pricing model: a simplified POS subscription plan. This innovative approach replaces the recurring monthly rental fees with a one-time setup fee, eliminating the need for ongoing charges. By shifting to this model, the bank aims to streamline operations, improve cash flow predictability, and increase revenue while offering merchants a simpler, more transparent payment structure. # Transforming POS Services with a One-Time Subscription Model The proposed approach aims to transform the traditional POS rental model into a one-time subscription service. This innovative approach focuses on determining the optimal upfront fee a merchant should be charged, taking into account lifetime monthly rentals and other associated charges. ## Understanding Merchant Relationships to Optimize Pricing To develop an effective pricing strategy, it's crucial to understand the nature of the bank's relationship with its merchants. This relationship fundamentally influences how we calculate a merchant's lifetime value (LT), which in turn informs the optimal pricing structure. 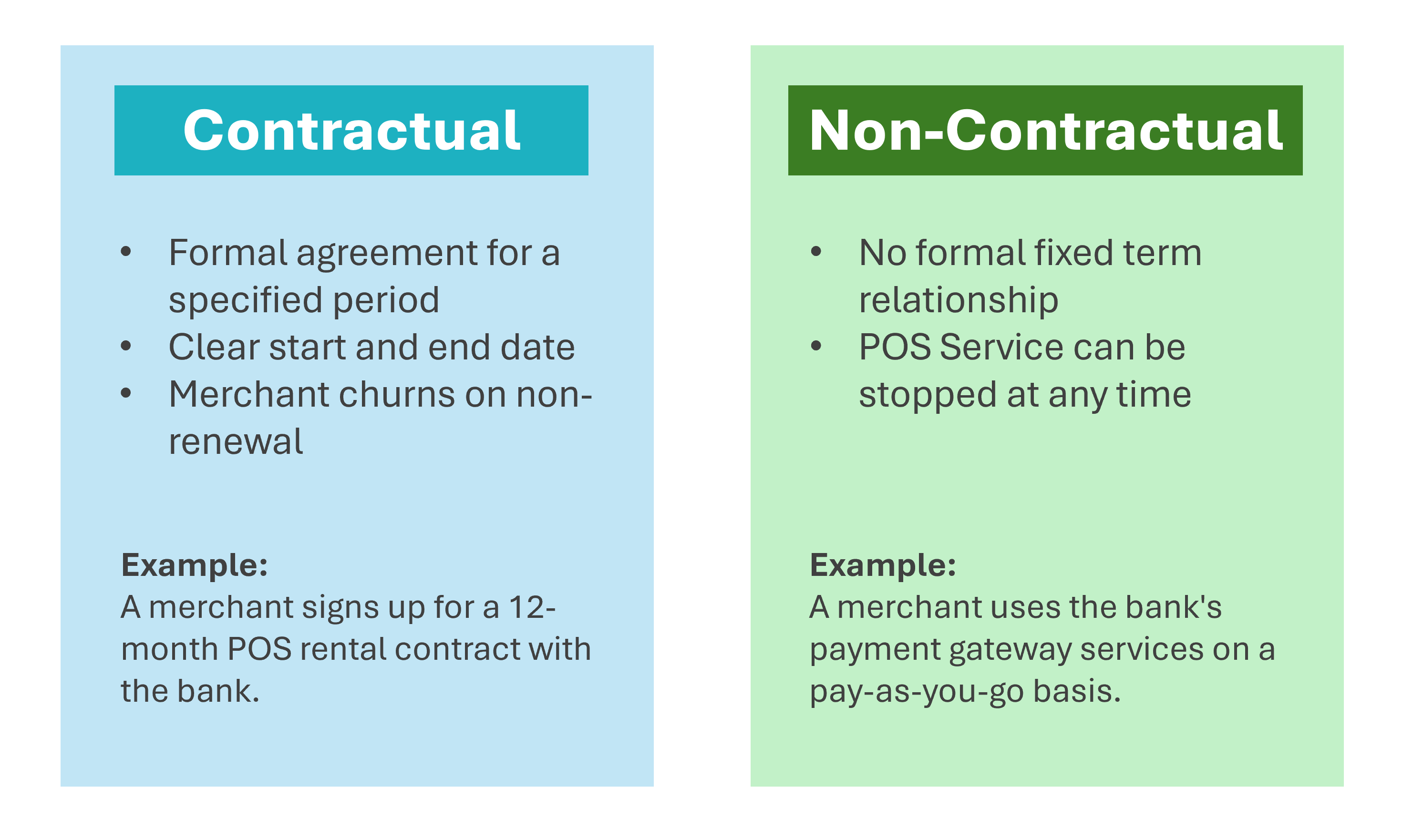In the context of POS services, merchant relationships with the bank can be categorized into two primary types: ![merchant-relationships.png](merchant-relationships.png) As seen in the visual above, merchant relationships can be broadly categorized as follows: - **Contractual**: Fixed-term agreements with defined start, end, and renewal points. - **Non-contractual**: Flexible arrangements without long-term commitments, allowing merchants to start or stop service use at will. In the case of POS rentals, the bank's relationship with merchants typically falls under the contractual type. Merchants are considered to have churned when they do not renew their contract or stop paying the monthly rental fee. This well-defined churn point makes it suitable for survival analysis techniques. In the rest of this case study, we will focus on the application of survival analysis techniques to optimize the one-time setup fee for contractual relationships. ## Calculating Lifetime Value for Contractual Relationships To determine the optimal approach for calculating Lifetime (LT) in contractual relationships, three techniques were explored: simple retention model, discrete time model, and Kaplan-Meier estimator. Our analysis found that the Kaplan-Meier estimator was best suited for our business problem. Below, we outline each method and explain why Kaplan-Meier was selected as the optimal solution. **1. Simple retention model** In this approach, LT is estimated as 1/Churn Rate. However, this method assumes a constant churn rate month-on-month, which did not align with the variability observed in our scenario. **2. Discrete time model** We fitted a logistic regression model using static independent variables such as demographics, merchant category, and declared annual turnover, along with the month of attrition. However, the model's accuracy and R-squared values remained low due to the limitation of using only these static variables. **3. Kaplan-Meier estimator** The Kaplan-Meier estimator is a non-parametric method for estimating survival probabilities in our merchant attrition scenario. These estimated probabilities can be used to calculate Merchant Lifetime (LT) as follows: $LT = \sum_{t=0}^{\infty} S(t)$ Where $S(t)$ is the survival function, representing the probability that a merchant will continue using the POS service beyond time $t$. The Kaplan-Meier estimator for the survival function in our context is given by: $\hat{S}(t) = \prod_{i: t_i \leq t} \left(1 - \frac{a_i}{m_i}\right)$ Where: - $t_i$ are the ordered attrition times - $a_i$ is the number of merchant attritions at time $t_i$ - $m_i$ is the number of merchants still using the service just prior to $t_i$ The probability of a merchant continuing service from one time point to the next is calculated as: $p_t = P(T > t | T \geq t) = \frac{S(t)}{S(t-1)}$ This method proved to be the most effective for our analysis of merchant attrition, as it doesn't rely on assumptions about the distribution of service durations and can handle the variability in our merchant data. It's worth noting that in our scenario, both Type I (fixed-time) and random right censoring apply. The Kaplan-Meier estimator naturally handles these types of censoring without requiring modifications to our calculations. For an explanation of right censoring and its implications, please refer to **Appendix A**. In the following section, we will provide a detailed example to demonstrate how the Kaplan-Meier estimator was applied to calculate Merchant Lifetime (LT) in our specific POS service context. ## Example: Calculating Survival Probabilities and Merchant Lifetime Let's consider a simplified example to illustrate how the Kaplan-Meier estimator can be used to calculate survival probabilities and Merchant Lifetime (LT) for POS terminal services. Note that these values are illustrative and not reflective of actual data. Suppose we have data for 100 merchants who started using POS terminals at the same time. We'll look at their status over a 6-month period. | Month ($t$) | Merchants at start ($m_t$) | Attritions ($a_t$) | | ----------- | -------------------------- | ------------------ | | 1 | 100 | 10 | | 2 | 90 | 10 | | 3 | 80 | 5 | | 4 | 75 | 10 | | 5 | 65 | 5 | | 6 | 60 | 5 | Note: At the end of month 6, the remaining 55 merchants are considered right-censored due to the study ending.

Step 1: Calculate Survival Probabilities

Using the Kaplan-Meier estimator, we calculate the survival probabilities $\hat{S}(t)$ for each month: $\hat{S}(t) = \prod_{i: t_i \leq t} \left(1 - \frac{a_i}{m_i}\right)$ 1. Month 1: $\hat{S}(1) = 1 - \frac{10}{100} = 0.900$ 2. Month 2: $\hat{S}(2) = 0.900 * (1 - \frac{10}{90}) = 0.900 * 0.889 = 0.800$ 3. Month 3: $\hat{S}(3) = 0.800 * (1 - \frac{5}{80}) = 0.800 * 0.9375 = 0.750$ 4. Month 4: $\hat{S}(4) = 0.750 * (1 - \frac{10}{75}) = 0.750 * 0.867 = 0.650$ 5. Month 5: $\hat{S}(5) = 0.650 * (1 - \frac{5}{65}) = 0.650 * 0.923 = 0.600$ 6. Month 6: $\hat{S}(6) = 0.600 * (1 - \frac{5}{60}) = 0.600 * 0.917 = 0.550$ Here's a detailed table showing the values at each month: | Month ($t$) | Merchants at start | Attritions | Survival Rate | Cumulative Survival Probability | | ----------- | ------------------ | ---------- | ------------- | ------------------------------- | | 0 | 100 | 0 | 1.000 | 1.00 | | 1 | 100 | 10 | 0.900 | 0.90 | | 2 | 90 | 10 | 0.889 | 0.800 | | 3 | 80 | 5 | 0.9375 | 0.75 | | 4 | 75 | 10 | 0.867 | 0.65 | | 5 | 65 | 5 | 0.923 | 0.60 | | 6 | 60 | 5 | 0.917 | 0.55 | Note: The survival rate for each month is calculated as $(1 - a_t/m_t)$, and the cumulative survival probability $\hat{S}(t)$ is the product of the current month's survival rate and all previous months' survival rates. See the following chart which plots the survival rates over time. ![survival_chart_example.svg](survival_chart_example.svg)

Step 2: Calculate Merchant Lifetime (LT)

The Merchant Lifetime (LT) is calculated as the sum of the survival probabilities: $LT = \sum_{t=0}^{\infty} \hat{S}(t)$ In our example, summing up to 6 months: $LT = 1 + 0.900 + 0.800 + 0.750 + 0.650 + 0.600 + 0.550 = 5.250$ months

Step 3: Calculate Lifetime Value (LTV)

Assuming a monthly rental fee of ₹2,000, the LTV would be: $LTV = LT$ _ Monthly Rental Fee = 5.250 × ₹2,000 = ₹10,500

Interpreting Results

1. On average, we expect a merchant to continue using the POS terminal for about 5.25 months. 2. The expected lifetime value of a merchant is ₹10,500. 3. This is a conservative estimate due to right-censoring at the end of the study period. 4. When pricing a one-time subscription, consider factors such as upfront costs, desired profit margin, and market conditions. For example, with upfront costs of ₹5,000 and a 20% profit margin target: Subscription Fee = ₹5,000 + ₹10,500 + (₹10,500 × 0.20) = ₹17,600 This simplified example demonstrates how the Kaplan-Meier estimator can be used to inform pricing strategies for POS terminal services, while accounting for the realities of merchant attrition and study limitations. # Implementing the Kaplan-Meier Estimator ## Dataset and Time Frame Merchant deactivations over a 12-month period were used to estimate Lifetime (LT). This timeframe provided a substantial dataset to capture various patterns of merchant behavior and attrition. ## Clustering for Differential LT Estimation For efficient LT estimation, the entire merchant base was divided into clusters based on various parameters such as geography, merchant operating category, annual turnover, and other relevant factors. Outlier treatment was performed on these clusters to ensure data quality. Through this process, approximately 20 clusters were formed by combining different levels of each clustering variable. This clustering approach allowed for a more nuanced analysis of merchant lifetimes across different segments of the business. The Kaplan-Meier estimator was applied to each cluster to calculate the survival function S(t) at each time point. Lifetime (LT) was then estimated using the following formula: $LT = \sum_{t=0}^{\infty} S(t)$ Where $S(t)$ represents the survival function, giving the probability that a merchant will continue using the POS service beyond time $t$. In practice, this summation is performed from $t=0$ to the last observed time point in our data. The following table shows illustrative results for several clusters: | Cluster # | Estimated LT (months) | | --------- | --------------------: | | Cluster 1 | 37.6 | | Cluster 2 | 41.4 | | Cluster 3 | 46.2 | | Cluster 4 | 39.1 | | Cluster 5 | 53.8 | | ... | ... | | ... | ... | | ... | ... | For each cluster, this method allowed for the calculation of cluster-specific lifetimes, which were found to range from 38 to 54 months, as illustrated in the table above. The variation in lifetimes across clusters highlights the importance of this segmented approach in capturing the diverse characteristics of different merchant groups. By applying the Kaplan-Meier estimator to each cluster separately, we were able to account for the unique attrition patterns within each segment of our merchant base. ## Validating the Model for Real-World Impact To ensure the reliability of the model, an out-of-time validation approach was employed. The cluster-wise lifetime (LT) estimates were validated using merchant deactivations from the subsequent 3 months. This method allowed the model to be tested on data not used in the initial estimation. The validation process achieved an accuracy of approximately 82%, with a tolerance for variation of ±3 months. This validation demonstrates the robustness of the Kaplan-Meier estimator in predicting merchant lifetimes, even when accounting for some variability in the exact timing of deactivations. The high accuracy supports the reliability of the model for business decision-making. # Immediate Business Impact: Revenue and Efficiency Gains The implementation of the one-time subscription fee model, based on the Kaplan-Meier lifetime estimation, has yielded significant immediate benefits: 1. **Revenue Generation**: Within the first 6 months, the model generated substantial upfront revenue from new-to-bank (NTB) merchants, representing a marked improvement over the previous monthly rental collection model. 2. **Improved Cash Flow**: By collecting fees upfront, the bank eliminated the need for monthly rental collections, reducing administrative overhead and improving cash flow predictability. 3. **Market Acceptance**: The model has been well-received by merchants, suggesting they see value in the simplified, one-time payment structure. 4. **Expansion Plans**: Given the initial success, plans are underway to extend this model to existing-to-bank (ETB) merchants, with strategic modifications to suit this segment. # Conclusion: A Data-Driven Revolution in Merchant Services The success of the one-time subscription fee model demonstrates the power of applying advanced statistical techniques to solve real-world financial challenges. This case study illustrates several key points: 1. **Data-Driven Innovation**: The application of the Kaplan-Meier estimator to merchant lifetime prediction showcases how data analysis can drive product innovation in financial services. 2. **Risk Mitigation**: The upfront fee structure reduces the bank's exposure to potential losses from merchant attrition, as the lifetime value is collected at the outset of the relationship. 3. **Competitive Advantage**: By offering a unique pricing model, the bank has differentiated itself in the competitive merchant services market, potentially attracting more merchants and increasing market share. 4. **Scalability and Adaptability**: The model's success with NTB merchants and planned expansion to ETB merchants demonstrates its scalability and adaptability to different customer segments. 5. **Future Potential**: This approach opens up possibilities for similar innovations in other areas of banking and financial services, where customer lifetime value plays a crucial role. This case study illustrates the potential for statistical modeling and data analysis to create tangible business value, improve customer experiences, and drive strategic decision-making in the banking sector. It serves as an example of how traditional financial institutions can advanced analytical methods to innovate within their existing business models and enhance their service offerings. # References 1. Discrete time survival models customer lifetime value: https://youtu.be/uFyYcgwyQFs?feature=shared 2. Klein, J. P., & Moeschberger, M. L. (2003). Survival analysis: techniques for censored and truncated data. Springer Science & Business Media. # Appendix ## A. Understanding Censoring in Survival Analysis In survival analysis, censoring occurs when we have incomplete information about the survival time of some individuals in the study. In the context of our POS terminal service, censoring happens when we don't observe the exact time a merchant stops using the service. Two types of right censoring are particularly relevant to our analysis: 1. Type I (fixed-time) censoring: This occurs when the study ends at a predetermined time. Any merchants still using the service at this point are right-censored, as we only know that their service duration exceeded the study period. 2. Random right censoring: This happens when merchants leave the study for reasons unrelated to the event of interest (stopping POS service). For example, if we lose contact with a merchant or if they go out of business for external reasons. The Kaplan-Meier estimator handles these types of censoring by: - Including censored observations in the risk set ($m_i$) up until their censoring time. - Not counting censored observations as attritions (they don't contribute to $a_i$). - Updating the survival probability only at times when attritions occur. This approach allows us to make use of the partial information provided by censored observations, leading to more accurate estimates of survival probabilities and merchant lifetimes. It's important to note that in the presence of heavy censoring, especially towards the end of the study period, the LT calculation may underestimate the true average lifetime. In such cases, the calculated LT effectively becomes a lower bound of the true lifetime. While there are other types of censoring in survival analysis (such as left censoring and interval censoring), these do not apply to our POS terminal service scenario. For readers interested in learning more about various types of censoring and their applications in survival analysis, we recommend referring to Klein and Moeschberger (2003) in References. ## B. Kaplan-Meier Estimator Calculation in Python ```python # Python code to calculate expected merchant lifetime using Kaplan-Meier estimator expected_lifetime = [] # Loop through 20 distinct merchant clusters for cluster_id in range(20): # Separate churned and censored merchants by cluster churned_merchants = df_comb2_ch[df_comb2_ch['Clust'] == cluster_id] censored_merchants = df_comb2[df_comb2['Clust'] == cluster_id] # Get survival times for churned and censored merchants churned_survival_times = churned_merchants['Surv_time'].to_list() censored_survival_times = censored_merchants['Surv_time'].to_list() # Sort survival times for both churned and censored merchants churned_survival_times.sort() censored_survival_times.sort() # Create a range of survival times from the minimum to the maximum in churned merchants time_range = range(int(churned_merchants['Surv_time'].min()), int(churned_merchants['Surv_time'].max()) + 1) # Dictionary to count occurrences of survival times for churned merchants churned_counts = {time: churned_survival_times.count(time) for time in time_range} # Dictionary to count occurrences of survival times for censored merchants censored_counts = {time: censored_survival_times.count(time) for time in time_range} # Initialize the total number of merchants and at-risk merchants n_total = len(churned_survival_times) n_at_risk = n_total # Initialize cumulative survival probability and list to store probabilities cumulative_prob = 1 survival_probabilities = [] # Loop through unique survival times to calculate Kaplan-Meier survival probabilities for time in time_range: churned_events = churned_counts[time] censored_events = censored_counts[time] # Calculate survival probability and update cumulative probability survival_prob = (n_at_risk - censored_events) / n_at_risk cumulative_prob *= survival_prob # Store cumulative survival probability survival_probabilities.append(cumulative_prob) # Update the number of at-risk merchants by subtracting churned events n_at_risk -= churned_events # Calculate expected lifetime for the current cluster by summing survival probabilities lifetime_estimate = sum(survival_probabilities) expected_lifetime.append(lifetime_estimate) ```