Survival analysis, often referred to as time-to-event analysis, is a critical tool in many domains, including economics, engineering, and especially medicine. This type of analysis is used to predict the time until the occurrence of an event of interest, such as equipment failure or death due to a specific disease. Traditional approaches to survival analysis, such as the Cox proportional hazards model, have been widely used for decades. However, these methods often rely on strong parametric assumptions that may not hold in real-world scenarios, particularly when dealing with competing risks—situations where multiple possible events could occur.
In the paper titled "DeepHit: A Deep Learning Approach to Survival Analysis with Competing Risks," the authors Changhee Lee, William R. Zame, Jinsung Yoon, and Mihaela van der Schaar present a novel approach to survival analysis that leverages the power of deep learning. DeepHit is a model that directly learns the distribution of survival times, without making any assumptions about the underlying stochastic processes. This blog will provide a comprehensive overview of the DeepHit model, including its architecture, the loss function used for training, and the results from experiments that demonstrate its effectiveness.
Survival analysis, also known as time-to-event analysis, is a statistical method used to analyze the expected duration of time until one or more events happen. This type of analysis is crucial in various fields, such as:
One of the most common models in survival analysis is the Cox proportional hazards model, which models the hazard function—a function that estimates the risk of an event occurring at time
In real-world scenarios, individuals or systems may be subject to more than one type of event, each of which could terminate the observation period. These scenarios are known as competing risks. For instance, in medical studies, a patient might die from different causes (e.g., cardiovascular disease or cancer). The presence of competing risks complicates survival analysis because the occurrence of one event (e.g., death from cardiovascular disease) precludes the occurrence of another event (e.g., death from cancer).
Traditional survival models often assume independence between risks or simplify the problem by considering only one event and treating others as censoring. This can lead to biased or incomplete analysis.
The DeepHit model is designed to address the limitations of traditional survival analysis methods by using deep learning to directly model the joint distribution of survival times and events, without relying on strong parametric assumptions.
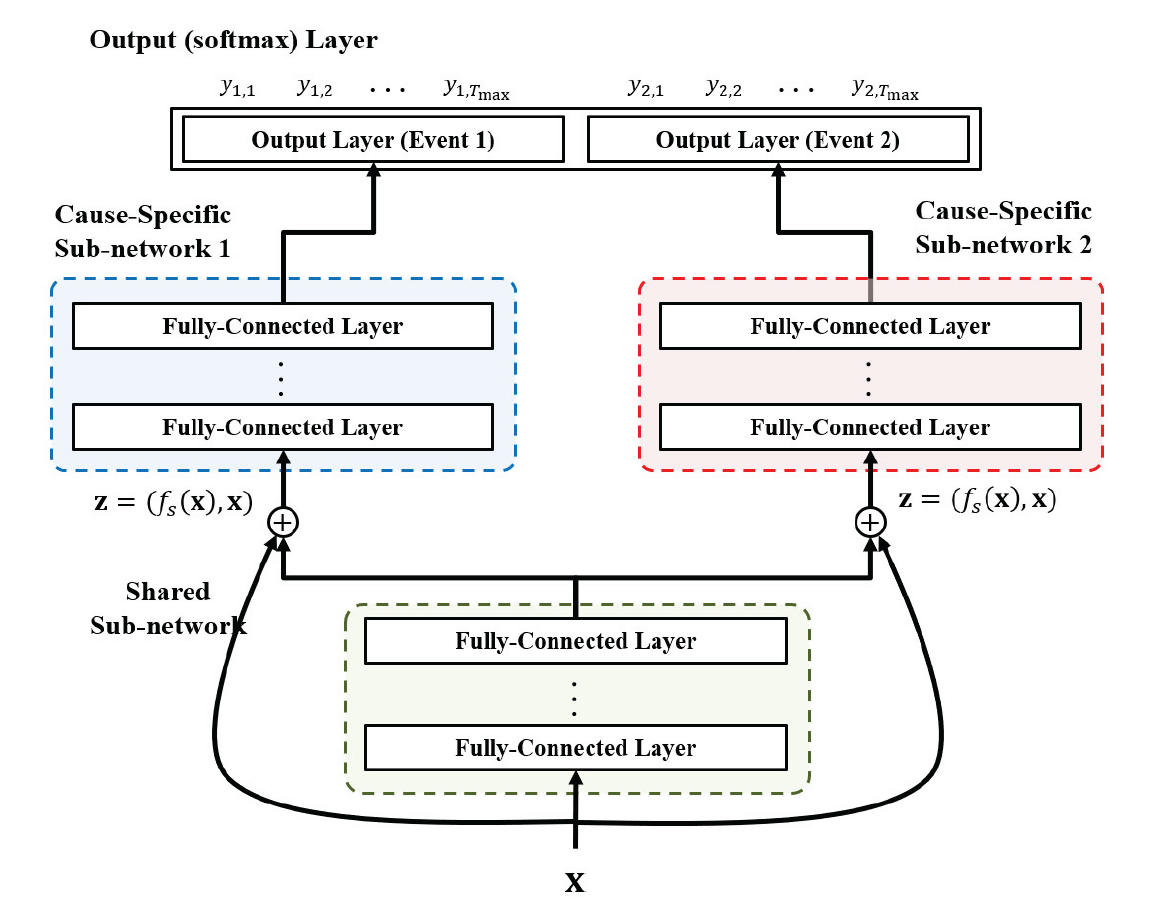
The DeepHit model consists of a neural network with the following structure:
Shared Sub-Network: This network is responsible for capturing the common features across all competing risks. It takes as input the covariates (features)
Cause-Specific Sub-Networks: Each event (or cause) has its own sub-network, which takes as input both the shared latent representation
Softmax Layer: The outputs of the cause-specific sub-networks are combined in a softmax layer, which produces the final probability distribution over the time-to-event for all possible events.
The DeepHit model aims to learn the joint distribution of the time-to-event and the event type, denoted by
To train the model, a custom loss function is designed to handle the unique challenges of survival data, such as right-censoring.
Log-Likelihood Loss
**Ranking Loss
risk. The idea is that if a patient (or subject) experiences an event earlier than another patient, then the predicted risk for the first patient should be higher. The ranking loss penalizes the model if this order is incorrect.
Here:
The total loss function is the sum of these two components:
This combined loss ensures that the model accurately predicts both the timing and the type of events, while appropriately handling censored data and encouraging correct ranking of risk.
DeepHit is trained using backpropagation and gradient descent. The network's parameters are adjusted to minimize the total loss
The training process involves feeding the network batches of patient data, each containing covariates, observed times, and event types (or censoring indicators). The network outputs the probability distribution over survival times for each possible event, and the loss is computed based on the discrepancy between the predictions and the actual data.
The performance of the DeepHit model is evaluated using the time-dependent concordance index (Ctd-index). This metric extends the traditional concordance index (C-index) to account for the time-varying nature of survival data. It measures the agreement between predicted and actual event times across the entire time horizon.
For each pair of patients, the Ctd-index compares their predicted survival times and the observed survival times. If the model consistently predicts higher risk (shorter survival time) for the patient who experiences the event earlier, the Ctd-index will be close to 1, indicating high predictive accuracy.
The authors of the DeepHit paper conducted extensive experiments to compare the performance of DeepHit with traditional and state-of-the-art survival models, including:
| Dataset | No. Uncensored | No. Censored | No. Features (real, categorical) | Event Time | Censoring Time |
|---|---|---|---|---|---|
| SEER CVD | 903 (1.3%) | 56,788 (83.1%) | 23 (7,16) | min 0, max 176, mean 79.8 | min 0, max 179, mean 144.6 |
| SEER BC | 10,634 (15.6%) | 5,668 (13.1%) | 23 (7,16) | min 0, max 177, mean 55.9 | min 0, max 177, mean 144.6 |
| UNOS | 29,436 (48.7%) | 30,964 (51.3%) | 50 (17,33) | min 0, max 331, mean 71.5 | min 1, max 331, mean 90.5 |
| METABRIC | 888 (44.8%) | 1,093 (55.2%) | 21 (6,15) | min 1, max 299, mean 77.8 | min 1, max 308, mean 116.0 |
A detailed discritpion of the datasets is provided in the folllowing table 1
Performance in Competing Risks:
Performance in Single Risk Scenarios:
In Table 2, The cause specific hazard concordance is compared for the SEER dataset, Table 3 shows the comparison for the synthetic dataset and Table 4 shows the comparison for the single event datasets.
| Algorithms | CVD | Breast Cancer |
|---|---|---|
| cs-Cox | 0.672 (0.664 - 0.680) | 0.639* (0.633 - 0.645) |
| Fine-Gray | 0.663‡ (0.656 - 0.670) | 0.639* (0.632 - 0.646) |
| DMGP | 0.657 (0.632 - 0.682) | 0.742‡ (0.738 - 0.746) |
| DeepHit (α = 0) | 0.674 (0.661 - 0.687) | 0.736 (0.733 - 0.739) |
| DeepHit | 0.684 (0.674 - 0.694) | 0.752 (0.748 - 0.756) |
* indicates p-value < 0.001
‡ indicates p-value < 0.05
| Algorithms | Event 1 | Event 2 |
|---|---|---|
| cs-Cox | 0.578* (0.570 - 0.586) | 0.588* (0.584 - 0.593) |
| Fine-Gray | 0.579* (0.572 - 0.586) | 0.589* (0.585 - 0.593) |
| DMGP | 0.663* (0.658 - 0.668) | 0.666* (0.660 - 0.672) |
| DeepHit (α = 0) | 0.739 (0.735 - 0.744) | 0.737 (0.732 - 0.742) |
| DeepHit | 0.755 (0.749 - 0.761) | 0.755 (0.748 - 0.762) |
* indicates p-value < 0.001
| Algorithms | UNOS | METABRIC |
|---|---|---|
| Cox | 0.566* (0.563 - 0.569) | 0.648† (0.634 - 0.662) |
| RSF | 0.575† (0.571 - 0.579) | 0.672 (0.655 - 0.689) |
| ThresReg | 0.571* (0.568 - 0.574) | 0.649† (0.633 - 0.665) |
| MP-RForest | 0.552* (0.548 - 0.556) | 0.650† (0.630 - 0.670) |
| MP-AdaBoost | 0.582 (0.578 - 0.586) | 0.633* (0.617 - 0.649) |
| MP-LogitR | 0.571* (0.567 - 0.575) | 0.661‡ (0.643 - 0.679) |
| DeepSurv | 0.563* (0.555 - 0.571) | 0.648† (0.636 - 0.660) |
| DeepHit (α = 0) | 0.573 (0.571 - 0.575) | 0.646 (0.634 - 0.658) |
| DeepHit | 0.589 (0.586 - 0.592) | 0.691 (0.679 - 0.703) |
* indicates p-value < 0.001
† indicates p-value < 0.01
‡ indicates p-value < 0.05
DeepHit’s core innovation is its ability to estimate the joint distribution of survival times and events. This is mathematically challenging because it requires simultaneously modeling the probability of different events over time. The neural network architecture allows for the flexible modeling of these distributions by learning complex relationships directly from data.
For each patient
A key concept in competing risks is the cumulative incidence function (CIF), which represents the probability that a particular event
DeepHit estimates the CIF by summing the predicted probabilities over time:
This allows DeepHit to compute the CIF for each cause, which is critical for making accurate predictions in the presence of competing risks.
DeepHit represents a significant advancement in survival analysis, offering a powerful tool for researchers and practitioners dealing with complex, real-world data. Its ability to handle multiple competing risks, model non-linear relationships, and provide accurate predictions even in the presence of censoring makes it a versatile and robust choice for survival analysis tasks.
The model’s performance in diverse datasets highlights its generalizability and potential for widespread application in medicine, engineering, and beyond. As deep learning continues to evolve, models like DeepHit are likely to become increasingly important, providing insights and predictions that were previously unattainable with traditional methods.
For those looking to implement or extend DeepHit, the authors have provided a solid foundation, but there are numerous avenues for further research, including exploring different network architectures, loss functions, and applications in new domains.
In summary, DeepHit is not just a step forward for survival analysis—it is a leap into the future, where deep learning enables us to tackle the most challenging predictive modeling problems with unprecedented accuracy and flexibility.