
Previous Article :-Mastering LLaMA
Previously, we explored the theoretical foundations of the LLaMA model, delving into its architecture and key components. Now, it’s time to put that knowledge into practice. In this article, we will implement the LLaMA model from scratch, translating the theoretical concepts into working code. By the end of this guide, you’ll have a solid understanding of how to build, train, and utilize a LLaMA model. Let’s get started!
@dataclass class ModelArgs: dim: int = 4096 n_layers: int = 32 n_heads: int = 32 n_kv_heads: Optional[int] = None vocab_size: int = -1 # set after loading the tokenizer multiple_of: int = 256 ffn_dim_multiplier: Optional[float] = None norm_eps: float = 1e-5 # Needed for KV cache max_batch_size: int = 32 max_seq_len: int = 2048 device: str = None
Define the model parameters first inside the class ModelArgs.
We have set the embedding dimensions to 4096, number of layers to 32, number of heads for the Queries to 32, number of heads for the Keys and Values to None. The multiple_of and ffn_dim_multiplier defines the dimension of the hidden layers.
def precompute_theta_pos_frequencies(head_dim: int, seq_len: int, device: str, theta: float = 10000.0): assert head_dim % 2 == 0, "Dimension must be divisible by 2" theta_numerator = torch.arange(0, head_dim, 2).float() theta = 1.0 / (theta ** (theta_numerator / head_dim)).to(device) # (Head_Dim / 2) m = torch.arange(seq_len, device=device) freqs = torch.outer(m, theta).float() freqs_complex = torch.polar(torch.ones_like(freqs), freqs) return freqs_complex
The theta parameter here is set as 1000 (taken from the paper). We need to check that the dimension of the word on which we are applying the embedding must be even because according to the paper we cannot apply this method on embeddings with odd dimension.
The shape of theta head according to the paper is set as (head_dim/2) and then we apply the formula.
Then we will calcuate all the possible theta for all the possible positions that our model will see.
Then using the outer method we will multiply m and theta such that the first element in m is multiplied with the first element of theta. Then we convert the frequency values to polar coordinates with magnitude 1.
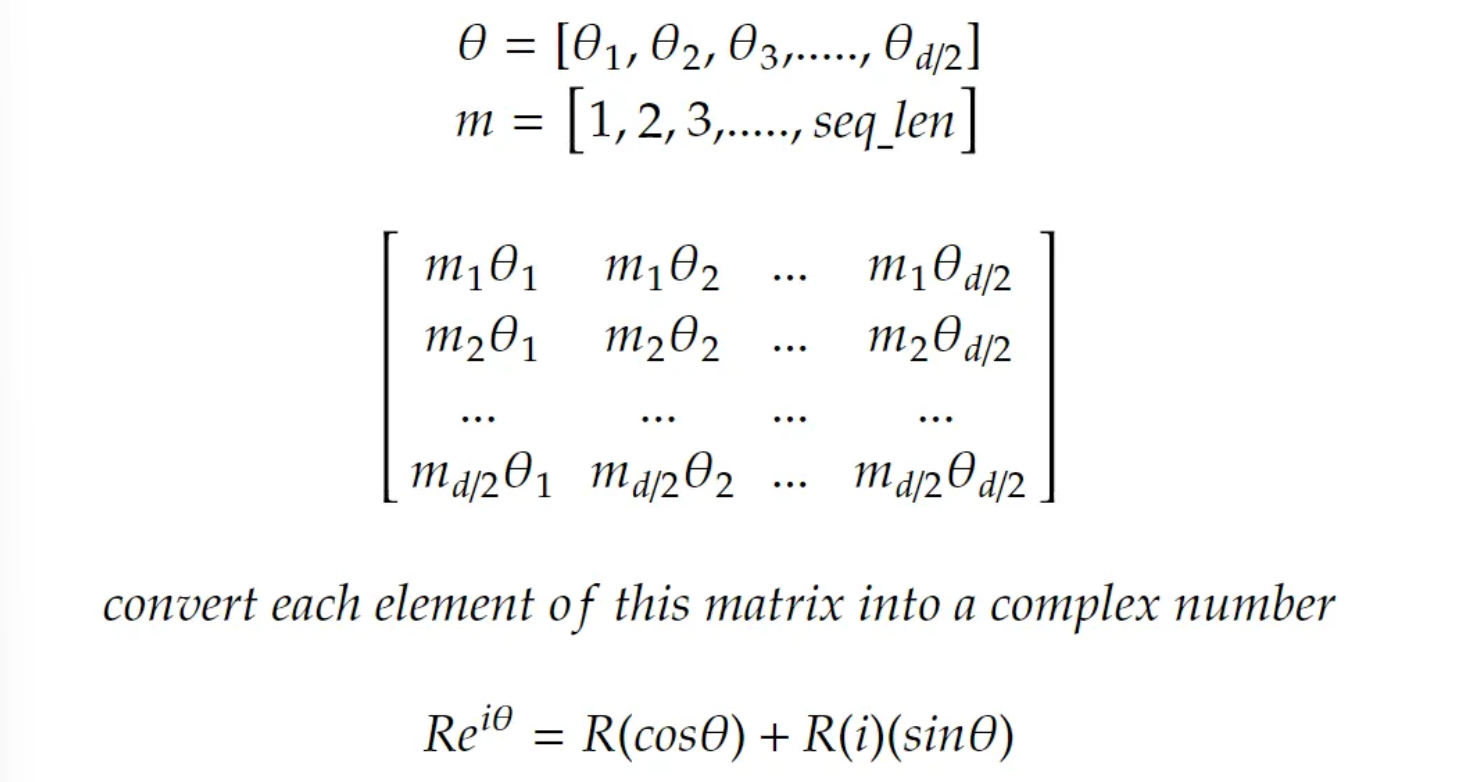
The matrix must be converted into a complex number hence we use polar function.
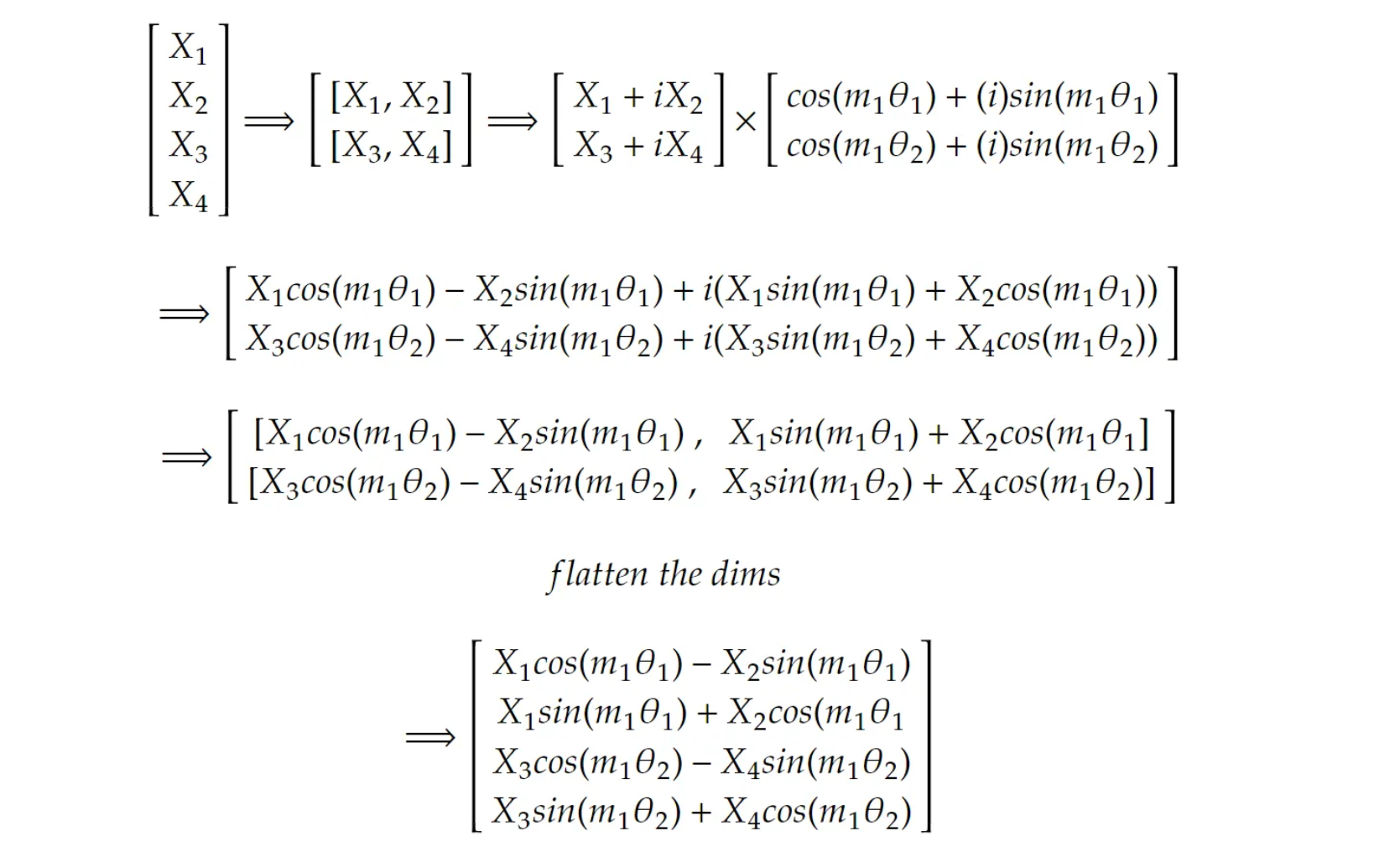
The above operation gives the resultant martix that we get after performing rotatory positional encodings.
def apply_rotary_embeddings(x: torch.Tensor, freqs_complex: torch.Tensor, device: str): x_complex = torch.view_as_complex(x.float().reshape(*x.shape[:-1], -1, 2)) freqs_complex = freqs_complex.unsqueeze(0).unsqueeze(2) x_rotated = x_complex * freqs_complex x_out = torch.view_as_real(x_rotated) x_out = x_out.reshape(*x.shape) return x_out.type_as(x).to(device)
Convert x to a float tensor if it is not already. Then reshape the tensor to have an additional dimension of size 2, which is necessary for converting it to a complex tensor. The resulting shape will be (batch_size, seq_len, head_dim/2, 2).
Then convert the reshaped tensor into a complex tensor. Each pair of real numbers is treated as the real and imaginary parts of a complex number. The resulting shape will be (batch_size, seq_len, head_dim/2).
Then add two singleton dimensions to freqs_complex, changing its shape from (seq_len, head_dim/2) to (1, seq_len, 1, head_dim/2). This allows for broadcasting when multiplying with x_complex.
x_complex * freqs_complex: Performs element-wise multiplication between the input complex tensor and the complex frequencies. This operation rotates the embeddings according to the positional encodings.
Then convert the complex tensor back to a real tensor with an additional dimension for the real and imaginary parteshapes.
class RMSNorm(nn.Module): def __init__(self, dim: int, eps: float = 1e-6): super().__init__() self.eps = eps self.weight = nn.Parameter(torch.ones(dim)) def _norm(self, x: torch.Tensor): return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps) def forward(self, x: torch.Tensor): return self.weight * self._norm(x.float()).type_as(x)
It normalizes the input tensor x by dividing it by the square root of the mean of its squared values (plus a small epsilon for numerical stability), then scales the normalized output by a learnable parameter weight. This normalization helps stabilize and accelerate the training of neural networks by ensuring that the inputs to each layer have similar distributions.
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor: batch_size, seq_len, n_kv_heads, head_dim = x.shape if n_rep == 1: return x return ( x[:, :, :, None, :] # (B, Seq_Len, N_KV_Heads, 1, Head_Dim) .expand(batch_size, seq_len, n_kv_heads, n_rep, head_dim) # (B, Seq_Len, N_KV_Heads, N_Rep, Head_Dim) .reshape(batch_size, seq_len, n_kv_heads * n_rep, head_dim) # (B, Seq_Len, N_KV_Heads * N_Rep, Head_Dim) ) class SelfAttention(nn.Module): def __init__(self, args: ModelArgs): super().__init__() self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads self.n_heads_q = args.n_heads self.n_rep = self.n_heads_q // self.n_kv_heads self.head_dim = args.dim // args.n_heads self.wq = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False) self.wk = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False) self.wv = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False) self.wo = nn.Linear(args.n_heads * self.head_dim, args.dim, bias=False) self.cache_k = torch.zeros((args.max_batch_size, args.max_seq_len, self.n_kv_heads, self.head_dim)) self.cache_v = torch.zeros((args.max_batch_size, args.max_seq_len, self.n_kv_heads, self.head_dim)) def forward(self, x: torch.Tensor, start_pos: int, freqs_complex: torch.Tensor): batch_size, seq_len, _ = x.shape xq = self.wq(x) # (B, 1, Dim) -> (B, 1, H_Q * Head_Dim) xk = self.wk(x) # (B, 1, Dim) -> (B, 1, H_KV * Head_Dim)) xv = self.wv(x) # (B, 1, Dim) -> (B, 1, H_KV * Head_Dim) xq = xq.view(batch_size, seq_len, self.n_heads_q, self.head_dim) # (B, 1, H_Q * Head_Dim) -> (B, 1, H_Q, Head_Dim) xk = xk.view(batch_size, seq_len, self.n_kv_heads, self.head_dim) # (B, 1, H_KV * Head_Dim) -> (B, 1, H_KV, Head_Dim) xv = xv.view(batch_size, seq_len, self.n_kv_heads, self.head_dim) # (B, 1, H_KV * Head_Dim) -> (B, 1, H_KV, Head_Dim) xq = apply_rotary_embeddings(xq, freqs_complex, device=x.device) # (B, 1, H_Q, Head_Dim) --> (B, 1, H_Q, Head_Dim) xk = apply_rotary_embeddings(xk, freqs_complex, device=x.device) # (B, 1, H_KV, Head_Dim) --> (B, 1, H_KV, Head_Dim) self.cache_k[:batch_size, start_pos : start_pos + seq_len] = xk self.cache_v[:batch_size, start_pos : start_pos + seq_len] = xv keys = self.cache_k[:batch_size, : start_pos + seq_len] # (B, Seq_Len_KV, H_KV, Head_Dim) values = self.cache_v[:batch_size, : start_pos + seq_len] # (B, Seq_Len_KV, H_KV, Head_Dim) keys = repeat_kv(keys, self.n_rep) # (B, Seq_Len_KV, H_KV, Head_Dim) --> (B, Seq_Len_KV, H_Q, Head_Dim) values = repeat_kv(values, self.n_rep) # (B, Seq_Len_KV, H_KV, Head_Dim) --> (B, Seq_Len_KV, H_Q, Head_Dim) xq = xq.transpose(1, 2) # (B, 1, H_Q, Head_Dim) -> (B, H_Q, 1, Head_Dim) keys = keys.transpose(1, 2) # (B, Seq_Len_KV, H_Q, Head_Dim) -> (B, H_Q, Seq_Len_KV, Head_Dim) values = values.transpose(1, 2) # (B, Seq_Len_KV, H_Q, Head_Dim) -> (B, H_Q, Seq_Len_KV, Head_Dim) scores = torch.matmul(xq, keys.transpose(2, 3)) / math.sqrt(self.head_dim) # (B, H_Q, 1, Head_Dim) @ (B, H_Q, Head_Dim, Seq_Len_KV) -> (B, H_Q, 1, Seq_Len_KV) scores = F.softmax(scores.float(), dim=-1).type_as(xq) # (B, H_Q, 1, Seq_Len_KV) -> (B, H_Q, 1, Seq_Len_KV) output = torch.matmul(scores, values) # (B, H_Q, 1, Seq_Len) @ (B, H_Q, Seq_Len_KV, Head_Dim) -> (B, H_Q, 1, Head_Dim) output = (output.transpose(1, 2).contiguous().view(batch_size, seq_len, -1)) # (B, H_Q, 1, Head_Dim) -> (B, 1, H_Q, Head_Dim) -> (B, 1, Dim) return self.wo(output) # (B, 1, Dim) -> (B, 1, Dim)
First we define number of heads for the Keys and Values then for the Queries, then n_rep is number of times the heads of K and V should be repeated to match the head of the Q. Then we define the weight metrices Wꟴ, Wᴷ, Wⱽ, Wᴼ. Then we will create cache one for the Keys and one for the Values. Then finally apply the forward function.
class FeedForward(nn.Module): def __init__( self, args: ModelArgs ): super().__init__() hidden_dim = 4 * args.dim hidden_dim = int(2 * hidden_dim / 3) if args.ffn_dim_multiplier is not None: hidden_dim = int(args.ffn_dim_multiplier * hidden_dim) hidden_dim = args.multiple_of * ((hidden_dim + args.multiple_of - 1) // args.multiple_of) self.w1 = nn.Linear(args.dim, hidden_dim, bias=False) self.w2 = nn.Linear(hidden_dim, args.dim, bias=False) self.w3 = nn.Linear(args.dim, hidden_dim, bias=False) def forward(self, x: torch.Tensor): swish = F.silu(self.w1(x)) # (B, Seq_Len, Dim) --> (B, Seq_Len, Hidden_Dim) x_V = self.w3(x) # (B, Seq_Len, Dim) --> (B, Seq_Len, Hidden_Dim) x = swish * x_V # (B, Seq_Len, Hidden_Dim) * (B, Seq_Len, Hidden_Dim) --> (B, Seq_Len, Hidden_Dim) x = self.w2(x) # (B, Seq_Len, Hidden_Dim) --> (B, Seq_Len, Dim) return x
Initially we are just rounding up the hidden dims to the nearest multiple of the multiple_of parameter. Suppose we have a hidden size of 7 and we want in multiple of 5 then we do (hidden + multiple — 1) → 7+4 = 11 and then divide this with multiple → 11/5 = 2. Then multiply the output again with multiple which will give 10. This is the first multiple bigger or equal to the hidden size.
Then we apply the SwiGLU function by implementing the formula given in its paper.
This block contains RMS Norm, Rotatory Positional Encodings, Self-Attetion, Skip Connections, again RMS Borm and Feed Forward Layers.
class EncoderBlock(nn.Module): def __init__(self, args: ModelArgs): super().__init__() self.n_heads = args.n_heads self.dim = args.dim self.head_dim = args.dim // args.n_heads self.attention = SelfAttention(args) self.feed_forward = FeedForward(args) self.attention_norm = RMSNorm(args.dim, eps=args.norm_eps) self.ffn_norm = RMSNorm(args.dim, eps=args.norm_eps) def forward(self, x: torch.Tensor, start_pos: int, freqs_complex: torch.Tensor): h = x + self.attention.forward( self.attention_norm(x), start_pos, freqs_complex ) out = h + self.feed_forward.forward(self.ffn_norm(h)) return out
Combine all the blocks to create the final LLaMA architecture.
class llamaModel(nn.Module): def __init__(self, args: ModelArgs): super().__init__() assert args.vocab_size != -1, "Vocab size must be set" self.args = args self.vocab_size = args.vocab_size self.n_layers = args.n_layers self.tok_embeddings = nn.Embedding(self.vocab_size, args.dim) self.layers = nn.ModuleList() for layer_id in range(args.n_layers): self.layers.append(EncoderBlock(args)) self.norm = RMSNorm(args.dim, eps=args.norm_eps) self.output = nn.Linear(args.dim, self.vocab_size, bias=False) self.freqs_complex = precompute_theta_pos_frequencies(self.args.dim // self.args.n_heads, self.args.max_seq_len * 2, device=self.args.device) def forward(self, tokens: torch.Tensor, start_pos: int): batch_size, seq_len = tokens.shape assert seq_len == 1, "Only one token at a time can be processed" h = self.tok_embeddings(tokens) freqs_complex = self.freqs_complex[start_pos:start_pos + seq_len] for layer in self.layers: h = layer(h, start_pos, freqs_complex) h = self.norm(h) output = self.output(h).float() return output
The n_layers parameter represents the number of times the Encoder block will get repeated 32 times. Here we have to recompute the frequencies of the rotatry positional encodings.
In the forward method we have set seq_len == 1 because we need to pass one token at a time, rest of them will be stored in KV Cache.
This class uses embeddings to convert tokens into dense vectors, passes them through multiple layers of EncoderBlocks, normalizes the final hidden states, and projects them to the vocabulary size to produce logits. Precomputed positional frequencies are used for rotary embeddings to incorporate positional information. The forward pass processes one token at a time and returns the output logits for the given token.
Next Article :- Training LLaMA