Abstract

Thanks to the advances in deep Reinforcement Learning (RL) and its demonstrated capabilities to perform complex tasks, the field of Multi-Agent RL (MARL) has recently undergone major developments. However, current MARL approaches based on deep learning still suffer from a general lack of interpretability. Recently, hybrid models combining Decision Trees (DTs) with simple leaves running Q-Learning have been proposed as an alternative to achieve high performance while preserving interpretability. However, efficient search strategies are needed to optimize such models. In this paper, we address this challenge by proposing a novel Quality-Diversity evolutionary optimization approach based on MAP-Elites. We test the method on a team-based game, on which we introduce a coach agent, also optimized via evolutionary search, to optimize the team creation during training. The proposed strategy is tested in conjunction with three different evolutionary selection methods ods and two different mappings between MAP-Elites archives and team members. Results demonstrate how the proposed approach can effectively find high-performing policies to accomplish the given task while the coach pushes even further the team

Introduction

Multi-Agent Reinforcement Learning (MARL) has received significant attention in recent decades, as it extends the applicability of traditional (single-agent) RL to problems where different agents must interact with each other and with a given environment. Typically, this results in a significantly more complex learn-
ing problem (compared to single-agent contexts), as in MARL the interactions between each single agent and the environment depend not only on the actions performed by that agent but also on what the other agents, which simultaneously interact with the same environment, do. Previous work addressed this challenge by employing Decision Trees (DTs) combined with RL in the context of MARL. Yet, this approach was limited to the fact that only one solution (i.e., one policy obtained as a DT with RL) was
generated. Another recent work, instead, showed that, in the case of single-agent RL tasks, applying a Quality-Diversity (QD) algorithm, specifically MAP-Elites (ME), can be an effective way to discover multiple DTs characterized by different depths and with different behaviors. In this work, we combine these two approaches and apply ME to derive multiple interpretable models for a MARL task. Furthermore, we propose the use of a “coach” agent to optimize team composition. This coach-based approach aims to enhance the trade-off between exploitation and exploration created by ME in order to fully exploit the characteristics of the evolutionary process. The paper describing the project has been accepted at Evostar2025.

Methodology

Figure 1 shows the whole process, illustrating how theselection methods and mapping strategies (see below for details) are set up in the tell and ask methods, which are important parts of our ME-based proposal. Our codebase is made publicly available on GitHub.
Each agent is formed by a DT combined with simple leaves running Q-Learning. The structure of the DT is optimized for ME, while IQL learns the optimal action for each leaf. The workflow is reported in the figure.

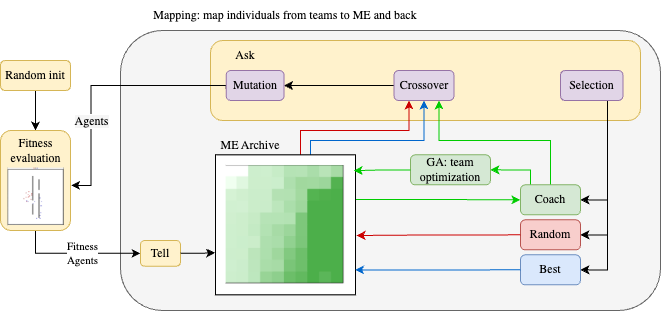
Our approach to optimizing the team selection process uses a coach agent that exploits MAP-Elites properties to optimally evolve sets of agents. The workflow of the agent can be described as follows:

1. The Coach collects the descriptors of the solutions with their corresponding fitness;
2. It optimizes k teams formed by m solutions via GA (with a population size of 100, uniform crossover with probability 1.0, Gaussian mutation with probability 0.1, and a maximum of 40000 generations), using the descriptors as “genes” and the n-percentile fitness of the solutions forming the teams as
   objective value;
3. For each optimized team, the Coach asks the corresponding solutions to the ME archive;
4. ME evolves the solutions and returns them to the Coach, to start the evaluation process.

The goal of using GA to select the optimal team is to efficiently achieve a trade-off between exploration and exploitation of solutions in order to increase the probability of having a higher number of optimal solutions stored in ME.

Experiments

Environment

Battlefield is a game environment specifically developed for testing MARL algorithms, available in the PettingZoo library. The game is based on two teams, blue and red, composed of 12 agents each. The goal of each team is to beat the other team by “killing” (i.e., removing from the environment) each member of it. In this work we optimize the policy of the blue team against a red team performing random actions at each step. The environment is an 80x80 grid, closed by outer walls that prevent the agents from exiting the game area; moreover, to make the task more challenging for the agents, there are 4 inner
walls as obstacles. The agents have the option to perform 21 different actions, namely taking no action, moving to one of the 8 nearby cells, attacking one of those cells, or moving two cells on either left, right, up, or down. Lastly, the reward is given by the performances during the task: each kill corresponds to 5 points; each attack carried out against an opponent corresponds to 0.9 points. The agent is penalized by−0.1 points for receiving hits, being killed, or attacking without hitting the enemy. In addition, at each step without other rewards, the agent loses −0.5 points.

Evaluations metrics

MAP-Elites evaluation The metrics that are most suitable for the purposes of our experiments concerning the archive coverage and the archive precision, which are defined as follows:
– Archive coverage It represents the percentage of the number of cells covered
by the algorithm out of the maximum number of cells in the grid.
– Archive precision Given the highest fitness found across all cells in a given run of ME, it represents the average error between the best fitness found in each cell and the highest fitness overall. Since the fitness values, in this case, are continuous variables, we consider the root mean square error (RMSE).
Fitness evaluation During the evaluation phase of the evolutionary process, a team consists of m agents that engage in a certain number of episodes, i.e., simulations of the task, denoted as Nep. Once the simulation is over, the fitness score is based on the agents’ rewards returned from the environment. To aggregate the rewards across episodes, we use n%-percentile, which was shown to achieve a trade-off between considering the maximum and the average performance across episodes.
Final team evaluation In the end, the algorithm stores the final optimal solutions to form the optimal team of agents. To evaluate the final teams, we test each formation derived from 10 executions of each approach in 100 new additional episodes. In this case, we evaluate these teams using three key metrics:
namely the average agent reward, the average number of kills, and the average task completion rate (along with the overall fitness of the team).

Research Questions

RQ1 Is ME a viable approach to solving MARL tasks?
RQ2 What is the effect that different selection strategies have on the evolution?
RQ3 Is it possible to interpret the optimized agents?

Results

RQ1 Is ME a viable approach to solving MARL tasks?

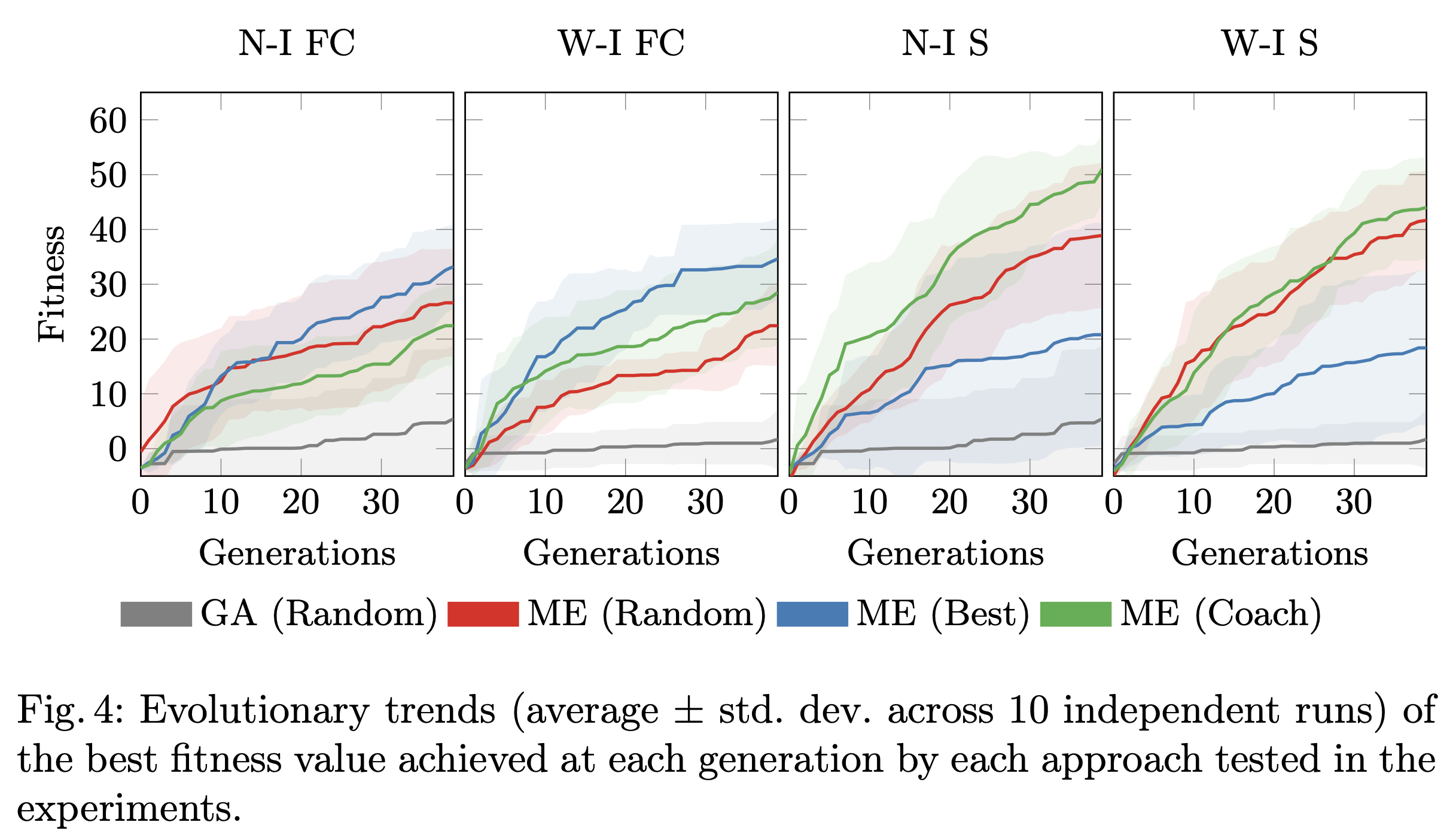
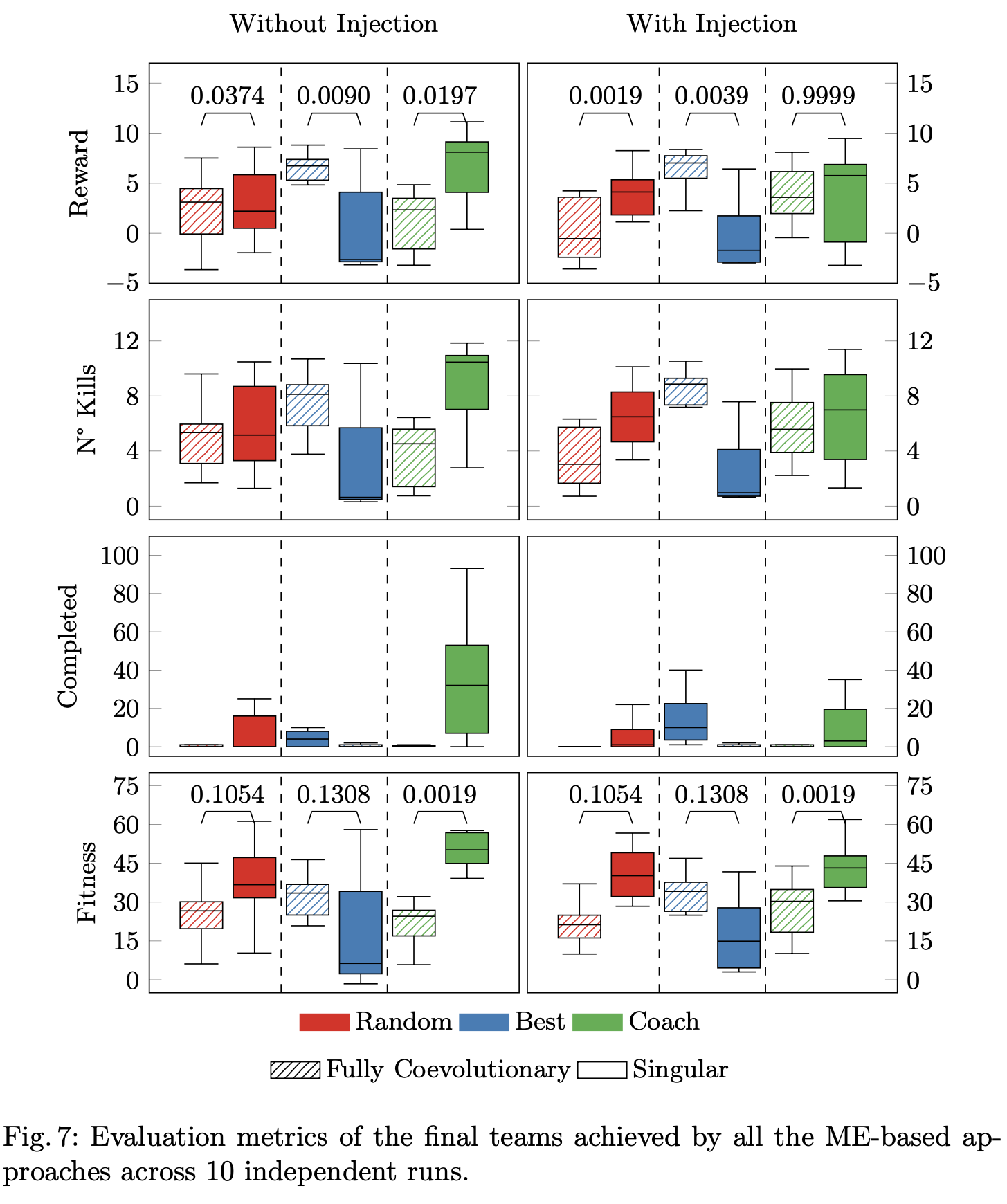
In Figure, we report the fitness trends during the generations of 10 independent runs of each approach tested in the experiments. While the baseline algorithm (based on GA) seems incapable of finding high-performing solutions (with fitness values below 10), the approaches using ME reach fitness values above 20. Exploiting ME in multi-agent reinforcement learning tasks can improve the overall performances.

RQ2 What is the effect that different selection strategies have on the evolution?

Our second analysis aims to evaluate ME using the three different selection mechanisms. To determine whether our proposal, i.e., the Coach selection, can indeed improve the trade-off between exploration and exploitation. In Figure, we show the best archives achieved across the 10 runs of each ME-based approach, where it is visible how the different approaches are characterized by different levels of
exploration-exploitation trade-off. In particular, Random shows a better exploration of the archive; Best achieves more exploitation with the singular mapping; whereas Coach produces several high-performing solutions in a more dense area than Random.

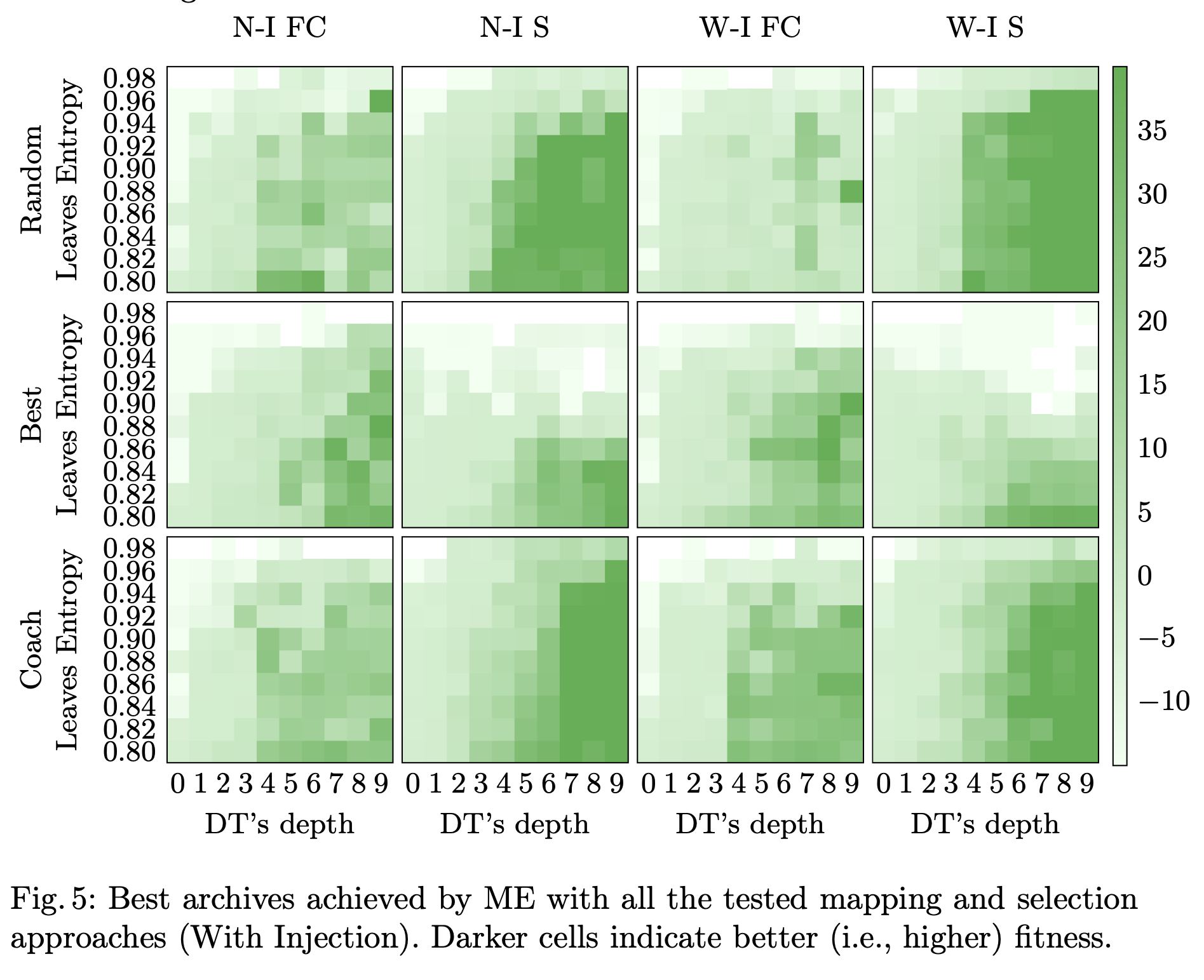
As for the singular mapping, it achieves the best results with Coach selection, which allows for higher exploration. This is Coach-Based Quality-Diversity for Multi-Agent Reinforcement Learning confirmed by the fact that Random (which is highly explorative) achieves higher coverage than Best in the case of Singular mapping. Overall, the best results in terms of archive coverage and precision are achieved by the Singular mapping with Coach and Random selection. Also in this case, we applied the Wilcoxon
signed-rank test (α= 0.05) to statistically confirm these findings, revealing that in all mapping settings Coach selection outperforms Best and Random with statistical significance.

RQ3 Is it possible to interpret the optimized agents?

The aim of the project was to develop a fully interpretable model. In the figure is reported the final structure of one of the agents forming the best-performing team, with the coach selection applied to a singular ME approach.

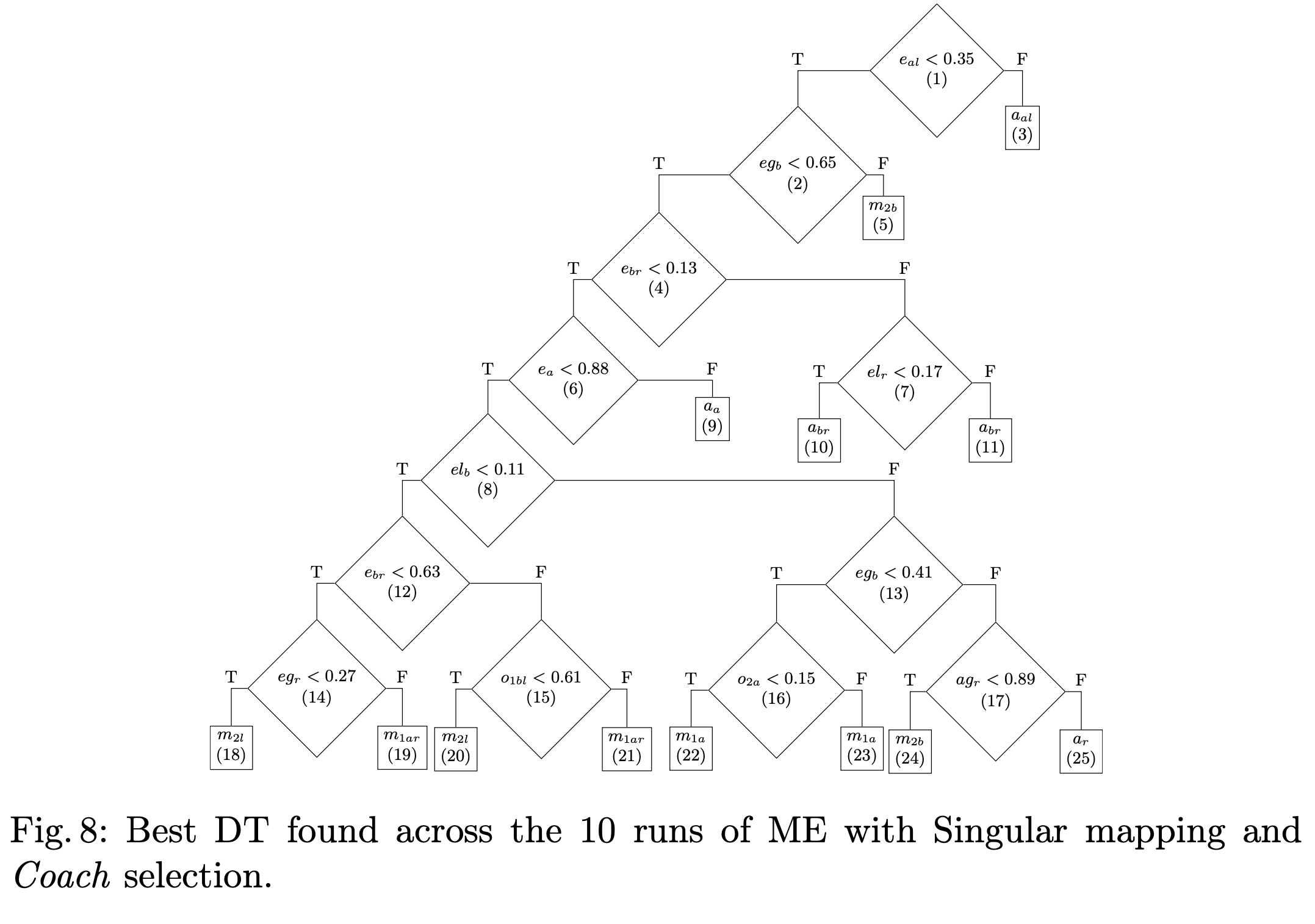
From the structure, it is possible to understand the reason behind a decided action by the agent. The sequence explains how the agent first navigates around the obstacle, which is initially below-left (id 15) and then above (id 16), by moving first left, then below, and finally above (id 20, 22, 24). Then it follows the enemy’s presence (id 14) by moving above (id 19). Occasionally, it adjusts the position to the right (id 19, 21). Then, it reaches the enemy from below (id 9), and it attacks 4 or 5 times (id 9). The episode
concludes with the agent adjusting its position (id 5, 19, 24) until it detects the presence of an enemy above (id 6). Then, it moves above (id 22) to attack the last remaining enemy three times (id 9).

Execute the project

The instructions on how to download and run the project and the models are reported on GitHub.

Conclusion

In this paper, we developed an evolutionary algorithm based on ME that optimizes the creation of teams to deal with MARL tasks. Considering agents based on a DT structure with leaves running Q-Learning, the proposed QD approach optimizes the structure of the DT, while RL learns the optimal actions to perform. Hence, it maintains high interpretability while returning high-performing solutions. In our experiments, we considered three selection mechanisms: two baselines, namely Random and Best selection, and then the proposed Coach selection, which uses a coach agent to supervise team formation. We also considered two ME mappings, namely fully coevolutionary and singular. The proposed Coach selection with Singular mapping revealed several advantages in terms of performance and computational complexity. In fact, it requires a reduced number of populations compared to Fully Coevolutionary mapping: the latter uses 12 populations, while Singular uses only one, besides the population for the coach agent. In terms of performance, this configuration outperformed all the other approaches in all evaluation metrics, still finding interpretable models.

Citing

If you like this project, we would appreciate it if you starred the GitHub repository in order to help us increase its visibility. Furthermore, if you find the framework useful in your research, we would be grateful if you could cite our publication, bibtex coming soon.

citing

Acknowledgements

I would like to thank Professor Giovanni Iacca and Andrea Ferigo, who led me into an interesting research topic and project, helping me to finalize the Master's degree in the best manner. Moreover, DIOL-UniTN, which is the perfect research environment to develop these ideas.