Abstract
The Principle of Maximum Entropy (MEP), first formalized by E.T. Jaynes, provides a powerful theoretical framework for addressing bias and uncertainty in probabilistic modeling. This article explores the largely unacknowledged yet evidently pervasive role of MEP in machine learning, highlighting its potential as a unifying principle for the field. By balancing uncertainty against known constraints, MEP aligns with foundational tasks in machine learning, such as regularization, Bayesian inference, and reinforcement learning.
We argue that MEP serves not only as a conceptual guide but also as an explanatory lens for understanding why certain methods—like stochastic gradient descent, overparameterization, soft actor-critic algorithms, and diffusion models—succeed. Moreover, the principle’s emphasis on maximizing learning opportunities within constraints positions it as a candidate for a broader "theory of machine learning."
This article examines the scientific foundations of MEP, connects it to practical applications across various machine learning methodologies, and discusses its limitations in high-dimensional and computationally constrained contexts. Finally, we advocate for increased exploration of MEP in machine learning research and practice, proposing that its systematic adoption could yield more principled and efficient approaches to model initialization, uncertainty quantification, and optimization.
One thing that is almost always in the back of the minds of machine learning practitioners and data scientists is how to construct less biased models. We want models to be objective and factual in their predictions and classifications. Prior distributions also need to integrate current information effectively without narrowly foreclosing on potentially enriching novel discoveries or getting trapped in local minima.
Mathematically, the problem of how to objectively avoid bias and calculate priors to maximize learning potential in the abstract is illuminated by the concepts of the principle of maximum entropy and the maximal entropy probability distribution, ideas which have been respected contributions to the scientific literature since the 1960s through the work of physicist and statistician E.T Jaynes [1].
The principle of maximum entropy asserts that subject to known constraints, the probability distribution that best represents our state of knowledge is the one with the highest entropy. That is to say, it’s the distribution with the highest uncertainty, or equivalently, one that makes the fewest assumptions or that rules out the fewest possibilities initially. The MEP essentially codifies the dictum, "be as open-minded as you can, while still respecting what you know for sure."
In essence, The MEP codifies the insight that, given what one knows the limits of what's possible, one should never rule out any possibilities that knowledge leaves open in order to best leverage the most informationally rich and open-ended learning opportunties. This relatively common sense axiom has broad implications when properly situated in a machine learning context.
Generally, the field of machine learning tends to be heavily empirical and results-driven. While this applied mindset is practical, theoretical insight into why various machine learning techniques work, or why such observations as the neural scaling effect hold, is lacking. This lack of a true theory of machine learning hampers empirical progress. We have incredibly powerful models, but we often lack theoretical guarantees about their behavior. We're often shooting in the dark when it comes to architecture design, regularization, and uncertainty quantification. With a proper theory of machine learning, practice can be better guided and informed, and reach more promising results within a clear framework of understanding.
I propose that the MEP and its related concepts could serve as a strong candidate for this "unified theory of machine learning", or gets us closer to one.
Rarely-and only recently- have researchers connected the maximum entropy principle to the machine learning domain. When researchers have investigated the maximum entropy concepts they often find broad and pervasive parallels and applications to a rich variety of machine learning topics. The MEP can be seen floating around the machine learning space, with some research and algorithms such as Soft-Actor Critic [2] Max Entropy Regularization [3] and Maximum-entropy Markov models [5] either explicitly built around it or tacitly incorporating it. Some researchers arguing that certain methods, such as Stochastic Gradient Descent (SGD), essentially embody it [4], and diffusion models naturally assume the maximal entropy state as their saturation point owing to their thermodynamic principles. It seems as though almost everywhere you look, this idea has some relevance or fits in some way.
I propose these forays into maximum entropy thinking for machine learning are just the tips of the iceberg. The MEP- this idea of always balancing uncertainty to known constraints, permeates machine learning and is a fundamental organizing principle of the field itself. On closer inspection, the MEP begins to look like the closest thing to a "scientific law" or universal generality we have in machine learning thus far.
To that end, here is a theoretical overview of MEP that draws parallels to its near ubiquitous and often understated role in machine learning. Despite largely this piece being largely theoretical in nature, several practical use cases of maximum entropy algorithms exist and will be briefly described, and more may be possible. Maximum entropy research could hold considerable future potential.
The format of this article is as follows:
1. To begin, we will have to work our way through some of the mathematical and scientific foundations of the MEP, with its roots in thermodynamics, probability theory, and information theory.
2. Then we will demonstrate some of its explanatory power by showing what areas of machine learning it unifies
3. We review some of its existing or potential applications
4. Following that, we'll discuss its practical, computational and mathematical limitations
5. We propose a conjecture that attempts to properly contextualize the scope and extent of the MEP's role in machine learning theory and practice
6. We close with a call to action for increased research interest in this MEP framework
Every probability distribution has a MaxEnt limiting case once known constraints are specified. The operative term is “known constraints.” For a distribution with no known constraints other than that the actual value is contained in the distribution’s support, the MaxEnt distribution is the uniform distribution. This limiting case of the MaxEnt principle as a whole is sometimes called the Principle of Indifference.
Intuitively, if you have three random variables A, B, and C, and know nothing about them at first other than that they are mutually exclusive (only one can be the "true" actual value) and no other alternatives to A, B, or C are in play, the most objectively unbiased initial prior probability distribution is one that assigns the same 1/3 = .3333… probability to each. The principle of indifference , or uniform distribution, is a kind of boundary condition for the MaxEnt principle in general-it's where you would start from if you had zero known constraints.
For a Bernoulli distribution, your known constraint would be:
For geometric:
and exponential, it would be:
and so on.
In principle, it's possible to calculate the maximal entropy distribution for any probability distribution with a bounded support or well-defined constraints.
In thermodynamic terms, you could think of this as the “truth particles” (random variables) of your probability density function equally diffused in a state of equilibrium throughout a “volume” (the distribution). Each distribution would effectively be a differently "shaped" volume. This analogy is far from superficial, as information theory has its roots in the same math as statistical mechanics.
Let's explore how the principle of maximum entropy illuminates this thermodynamic analogy of probability distributions. This connects beautifully to both statistical mechanics and information theory through the concept of entropy.
In thermodynamics, entropy measures the number of possible microscopic arrangements (microstates) that could give rise to the same macroscopic properties (macrostate). A system naturally evolves toward the macrostate with the most possible microstates - the maximum entropy state - subject to whatever constraints are present.
When we apply this thinking to probability distributions, we can see why the principle of maximum entropy makes deep theoretical sense. Just as a gas will diffuse to fill its container uniformly (maximizing entropy) unless constrained, our probability distribution should spread out as much as possible while respecting any known constraints.
Let's break this down step by step:
In our probability "volume", each possible configuration of the random variables represents a microstate. The overall shape of the probability distribution represents the macrostate.
Just as particles in a gas will spread out evenly in space unless constrained, our probability mass should spread out evenly across all possible outcomes unless we have specific information (constraints) telling us otherwise.
The mathematical form of entropy in both cases measures this "spread":
These forms are fundamentally the same - they both measure the logarithm of the number of possible arrangements.
So when we apply maximum entropy to find a probability distribution, we're essentially asking: "What's the most spread-out distribution possible that still satisfies what we know?" This gives us the distribution that:
For example, if we only know the mean of a continuous distribution, the maximum entropy principle tells us the distribution must be Gaussian. If we only know that a variable is positive with a known mean, we get an exponential distribution. These aren't arbitrary choices - they're the most "spread out" distributions possible given those constraints.
(N.B The math over distributions of continuous variables gets a bit hairy, and you can end up with infinite entropy, rendering the concept impractical if naively applied. I talk a bit more about this in the "limitations" section below.)
To connect this back to machine learning, let's talk a little bit about how randomness is often "employed." In innumerable machine learning tasks, we're generally concerned with the discovery of an approximation of an unknown function that satisfies a predictive or classificatory problem defined over a dataset. We tend to apply machine learning to problems which we can't solve ourselves for whatever reasons-so we're almost always dealing with some degree of uncertainty. Overfitting a model is equivalent to settling on a too low of an entropy solution. It lacks flexibility as the system loses the ability to map transformations to variations of the same class or problem. When we use regularization or similar methods to improve the situation, we're effectively tossing in some entropy to help break the model out of overly fixated patterns. The randomness we employ is not as ideal as applying knowledge to help instruct the model-but if we had that knowledge, we'd not be using machine learning! So we use randomness-within constraints- to inject some volatility into the search process, in the hopes that this advances the learning process.
The MEP tells us what kinds of uncertainty to throw into such computations, since it is only what is uncertain relative to known constraints, and therefore only what could possibly be true. It's not pure randomness in the literal sense. This is a powerful concept.
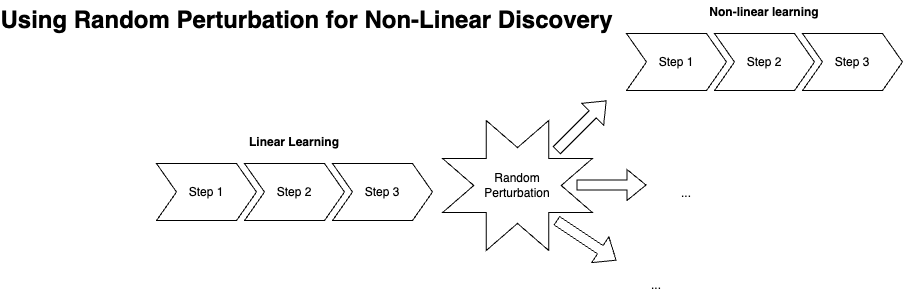
The maximum entropy framework provides a principled way to think about how much regularization to apply. Rather than treating regularization as just a practical tool to prevent overfitting, we can view it as implementing a fundamental principle: use the highest entropy solution that's consistent with our known constraints (in this case, our training data and prior knowledge about the problem structure).
Similarly, maximum entropy helps us contextualize under-fitting. By calculating the maximum entropy of a dataset—representing the theoretical upper bound of uncertainty—we can determine whether a model is under-fit by comparing its predictive entropy or residual entropy to this maximum. A model close to the maximum entropy may indicate under-fitting, as it suggests a high uncertainty model that has not captured enough structure from the data. (However, this comparison should account for the inherent uncertainty in the dataset, as some tasks naturally have high entropy even when well-fitted.)
The MaxEnt perspective suggests an elegant definition for what we mean by “learning” in machine learning (and perhaps in general). MaxEnt suggests learning is simply the reduction of excess entropy—the exclusion of irrelevant computational possibilities from the current estimate, reflected as a “gain in confidence” encoded into the continuously refining learned parameters of the model. Learning is "emptying out", everything you don't need within a space of uncertain possibilities, leaving only what you do need. This is more than a simplistic trial and error depiction, however, since the more you learn the more you reshape the outlay of what's possible for future learning (by updating constraints in a directed fashion).
Occasionally, learning can also mean the controlled “release” of entropy within known constraints, in the case of regularization during overfitting, when new areas of possibility need to be explored to counteract premature restrictions on the bounds of the solution space. Periodically, we may want to also update our known constraints and recompute the outlay of maximally entropic probabilities relative to them.
But in an idealized-not necessarily realistic-MaxEnt ML workflow, all learning would be reductive (starting from relatively disordered values and shrinking to ordered values), which is conceptually elegant. MaxEnt suggests a steady "cast a wide net, then reel in" workflow.
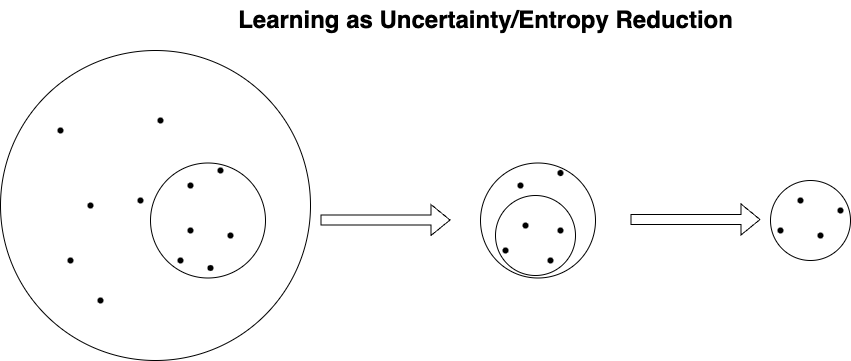
The MEP tells us how to determine the upper bounds of the search space considering known constraints, ensuring that our targets are always within distribution.
The MEP also tells us why despite efforts at optimization, machine learning techniques always tend to be computationally expensive relative to almost everything else we do with computers. The "no free lunch" principle is a corollary to the need to assume explorable uncertainty within known constraints to discover an approximation of an unknown function.
Indeed, if taken at face value, the principle of maximum entropy suggests that the essence of machine learning can be summed up as:
Maximize Learning Opportunities Under Known Constraints and Update Constraints in Response to Successful Learning.
That is to say, it seems to suggest machine learning is an exercise in entropy maximization (within the constraints of prior estimations) and constraint satisfaction, followed by an update on prior estimates using posterior probabilities to reflect the new known constraints earned from that learning.
Many modern machine learning techniques can be seen as—perhaps even unwittingly—approximations of a MaxEnt principle under certain constraints. Or, put differently, the MaxEnt principle is a rough first pass on these techniques. Below are some examples:
Researchers argue the overparameterization of DNNs allows them to represent many possible solutions for a given task. Among these solutions, entropy maximization guides the network to choose those with the least amount of unwarranted bias (i.e., the solutions with the highest entropy). [4]
Data augmentations of visual inputs can be seen as applications of group transformations over an approximate maximal entropy dataset, in order to detect invariances [1]. Put differently, a CNN that achieves rotational invariance under its theoretical maximal entropy distribution could be seen as "complete" within its constraints. Each rotation is a state in the maximum entropy configuration space, and sufficient data augmentation achieves saturation within this space. When we apply group transformations over a maximum entropy distribution, we're essentially saying "these are ALL the ways our assumptions allow the world to vary."
While not exclusively a machine learning concept, genetic and evolutionary algorithms tacitly reflect maximum entropy thinking. Random mutation happens under the "known constraints" of selection pressures, ensuring that we can progressively build structure from "constrained noise" over time.
Diffusion processes, being thermodynamically inspired by their nature, naturally assume the maximal entropy distribution as their saturation point or extremum. What makes this particularly interesting is that diffusion models essentially implement the maximal entropy principle twice:
In the forward process, they explicitly maximize entropy by adding noise until reaching a known maximum entropy distribution (Gaussian).
In the reverse process, they implicitly maintain maximum entropy subject to the learned constraints of the data distribution. At each denoising step t, the model produces a distribution that has the highest entropy possible while still being consistent with what it has learned about the structure of real data.
The MEP has much to teach us about how to approach sampling objectively in general. It suggests that rather than taking a random sample in the absence of informed priors, there may be more comprehensive ways to sample a distribution for training and testing that is designed to cover the full range of possibilities over a dataset.
As can be seen from the examples above, many methodologies considered “least biased” or “uninformative,” or "well chosen" in actuality pay homage to the MaxEnt Principle or apply it either implicitly or explicitly. MaxEnt explains why certain distributions, techniques, or initializations appear frequently. In a field starved for explanation, this is a major insight.
Aside from a simple lack of awareness, there are other reasons why the MEP is not a commonplace in machine learning teaching and practice. Why not always use the MaxEnt distribution as the objectively most unbiased and information rich prior and then “drill down”? The reasons are several:
Initializing to the MaxEnt distribution would be overkill for many projects that incorporate domain knowledge or fine-tuned research insight into the setup. The concept is most useful when informed priors are unavailable or when open-ended exploration is preferred .
Most nontrivial ML projects deal with large high-dimensional datasets, and thus the true MaxEnt distribution would be astronomical. For many practical use cases, MaxEnt is only approximated as "more entropy" (Ent+). For such datasets would not want to literally generate the MaxEnt distribution and then "pick through it". (However, the coarse boundaries and statistics of the MaxEnt distribution can be calculated cheaply, "on the back of a napkin" and used as a frame of reference.)
Bias mitigation and prior selection aren't the only concerns of ML engineering, which often has to concern purely practical constraints such as GPU usage. If they come at the expense of other priorities, such as optimization, they may need to take a backseat. Sometimes, it would be simply be overly indulgent to assume a more entropic, let alone a maximally entropic condition unnecessarily.
Entropy-as the degree of uncertainty of a probability distribution-is not necessarily valuable and usable in its own right. At best, it correlates with complexity or variation-themselves only correlated with interestingness or usability. At worst, it's just random noise. We use information entropy in the hopes that it helps us discover unknown and useful complexity, but it is a volatile substance. Without optimization mechanisms (Bayesian principles seem to pair well) MaxEnt methods can be wasteful.
A hard mathematical limit to the practical utility of the Maximum Entropy Principle (MEP) applies to distributions with unbounded support (e.g., (-∞ to +∞)), as the entropy may diverge to infinity or become computationally intractable. Even for well-behaved distributions like the Gaussian, the entropy calculation assumes an idealized continuous domain, which is not feasible in real-world computation. In machine learning, unbounded domains are typically clipped or truncated to make the problem computationally manageable. However, this truncation imposes artificial constraints, effectively altering the MaxEnt solution and potentially introducing bias. The need to truncate or discretize approximations of the MaxEnt distribution highlights its often approximative use involving continuous domains.
The curse of dimensionality also underscores a subtle point: a fine line exists between known constraint and bias. When dealing with large, complex datasets, we’re usually trying to find the relative MaxEnt distribution as “allowed” by computational constraints. This “allowed” distribution may not be the True MaxEnt distribution, but it’s the best approximation of it we can feasibly manage. Arguably many initialization and regularization techniques are essentially seeking this “allowed” sweet spot. Constraint selection is crucial to any maximum entropy technique, and an inappropriate choice could throw everything off. If the proper constraints are not selected, then we'll have effectively introduced bias in the effort to remove it.
The MEP is intended for probability distributions. While probability distributions are pervasive in the statistical modeling central to mainstream machine learning concepts, they aren't an a priori necessary condition for it. While comparatively little progress has been made in this deterministic AI front (e.g. rule-based systems, symbolic AI), deterministic machine learning might be possible. As a method of uncertainty quantification the MEP would be of no apparent use for these predictable programs.
These limitations clearly show why the MEP can't be penciled in as an unquestionable "law of gravity" of machine learning without footnotes and caveats. That said, these limits speak to matters of the computational feasibly of the principle applied to certain problems rather than its overall mathematical soundness.
While I can’t prove it, one could even see the opportunity to propose a conjecture: any carefully considered initialization will approximate the MaxEnt principle so far as is computationally feasible. The key word here is “approximate”, since the goal of any machine learning model is to shed as much unnecessary entropy as possible, and only allow enough to permit some flexibility and adaptive potential to the system’s future learning potential and to therefore strike the right balance between order and chaos. The second key phrase is “computationally feasible”, since in practice, working with the true MaxEnt distribution for the typically large datasets of machine learning is often intractable.
I find the reasoning behind this conjecture simple and elegant.
Conclusion: Finally, while you may not always assume the maximum entropy distribution according to this reasoning, you'd always want to take the Ent+ distribution; you'd always want to-or have to- take on more resources than you'll eventually need. This grow and prune strategy appears often in nature: newborns are born with many more neurons than they will eventually end up with, since this overproduction equips their brains with all the degrees of freedom they would ever need to adapt to whatever they might experience. And in general, pretty much all serious ML applications over-consume computational resources in the process of honing in on their targets, making their computations inherently entropic. Overabundance is a better problem to have to deal with than scarcity when you don't know how much resources you'll need. This thinking is embodied in the proverbial "throw stuff at the wall and see what sticks" approach.
At the end of the day, for most practical situations domain knowledge often trumps theoretical purity when constraints are well understood. Nevertheless, the MaxEnt Principle is an insightful theoretical baseline to contextualize our machine learning explorations. It reminds us what we’re truly doing with machine learning: sorting through and reducing vast spaces of irrelevant possibilities in search of thin bands of useful structure that fit the constraints of our datasets and requirements. It's helpful to know everything we do happens against the backdrop of this ceiling of maximum entropy. It forms, as it were, a "meta-constraint" on the field itself.
One main reason why the MaxEnt principle is relatively obscure despite being an implicit theme to so much machine learning work is the degree to which “known constraints” and informed priors play an oversized role in applied machine learning. Prior experience, research, and best practices cluster around certain techniques and tools, making whatever implicit MaxEnt thinking hinted at almost imperceptible.
MaxEnt avoids bias in the starting point, but in practice subsequent optimization relies on data and the loss function to guide the model toward useful solutions. In effect, to get anything done we have to treat a model's search space as a closed system, even though, just as the physicists say, "the only truly closed system is the universe as a whole."
One could argue against this story I'm telling by claiming that I'm essentially mesmerizing myself into seeing a general truth everywhere in a specific case to which it applies and mistaking the truth to be specially "made for" that case. In other words, of course the MEP, as the codification of common sense precept of rationality would apply to machine learning. Machine learning is a rational enterprise that would naturally inherit the traits of sound reasoning. One could expand the critique to say that it's just information theory that's the proper basis of a theory of machine learning, and the MEP is just an extension of information theory.
I'd argue against this by weighing the specificity of the insights the MEP gives us with respect to improbably many highly niche applications which could otherwise assume any other possible interpretation if left to chance. "Maximizing learning opportunities relative to known constraints" is a definition that is uniquely contoured to learning and search problems.
None of this is to suggest that MaxEnt is the whole piece of a unified theory of machine learning. In a field as complex and variegated as machine learning a single answer for everything is unlikely. Nevertheless, its systematic and repeated appearance across various methodologies, techniques, and applications warrants more attention and further investigation.
The MEP provides us with a formalized means to determine how much uncertainty we should take on in our models considering known constraints and the boundaries of the problem space. As such it serves as a kind of "ceiling" for the field. However, it doesn't tell us how to certify what constraints we adopt, or how to select the fewest, but most valid assumptions. If the wrong constraints are chosen, the MEP fails completely. Constraint selection is obviously nontrivial. One might therefore imagine a complementary, "minimum information principle" to serve as a corresponding "floor" to help explain this side of machine learning theory left unaddressed by the MEP. For any problem space, is there a principle mechanism to calculate, without the need for fine tuning the question presupposes, the appropriate hyper-parameters as minimum viable information constraints?
Incorporating MaxEnt reasoning and the MEP particularly into our work allows us to set up better conditions to let the data “speak for itself.” While the practical utility of MaxEnt is usually only approximative, considering the lack of a systematic research program around it, it could be more useful than is currently appreciated. I would advocate for increased research interest into the topic and for its more widespread adoption and awareness among educators and the ML research community. The Principle of Maximum Entropy and the family of concepts under its umbrella provides a strong framework for much machine learning theory and practice.
[1] E. T. Jaynes, "Prior Probabilities," in IEEE Transactions on Systems Science and Cybernetics, vol. 4, no. 3, pp. 227-241, Sept. 1968, doi: 10.1109/TSSC.1968.300117.
[2]Haarnoja, T., Zhou, A., Abbeel, P., & Levine, S. (2018). Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv preprint arXiv:1801.01290. Available at: https://arxiv.org/abs/1801.01290.
[3] Kim, D., Bae, J., Jo, Y., & Choi, J. (2019). Incremental Learning with Maximum Entropy Regularization: Rethinking Forgetting and Intransigence. arXiv preprint. Available at: arXiv:1902.00829v1.
[4] Guanhua Zheng, Jitao Sang, and Changsheng Xu. Understanding Deep Learning Generalization by Maximum Entropy. Published as a conference paper at ICLR 2018. Available at arXiv:1711.07758v1.
[5] Toutanova, Kristina; Manning, Christopher D. (2000). "Enriching the Knowledge Sources Used in a Maximum Entropy Part-of-Speech Tagger". Proc. J. SIGDAT Conf. on Empirical Methods in NLP and Very Large Corpora (EMNLP/VLC-2000). pp. 63–70.
There are no models linked
There are no models linked
There are no datasets linked
There are no datasets linked
