Before Transformers, Recurrent Neural Networks (RNNs) were used to handle sequence-to-sequence tasks. RNNs process sequences by maintaining a hidden state, allowing them to map an input sequence to an output sequence over several time steps. At each time step, an input token and the hidden state from the previous step are fed into the RNN to produce an output.
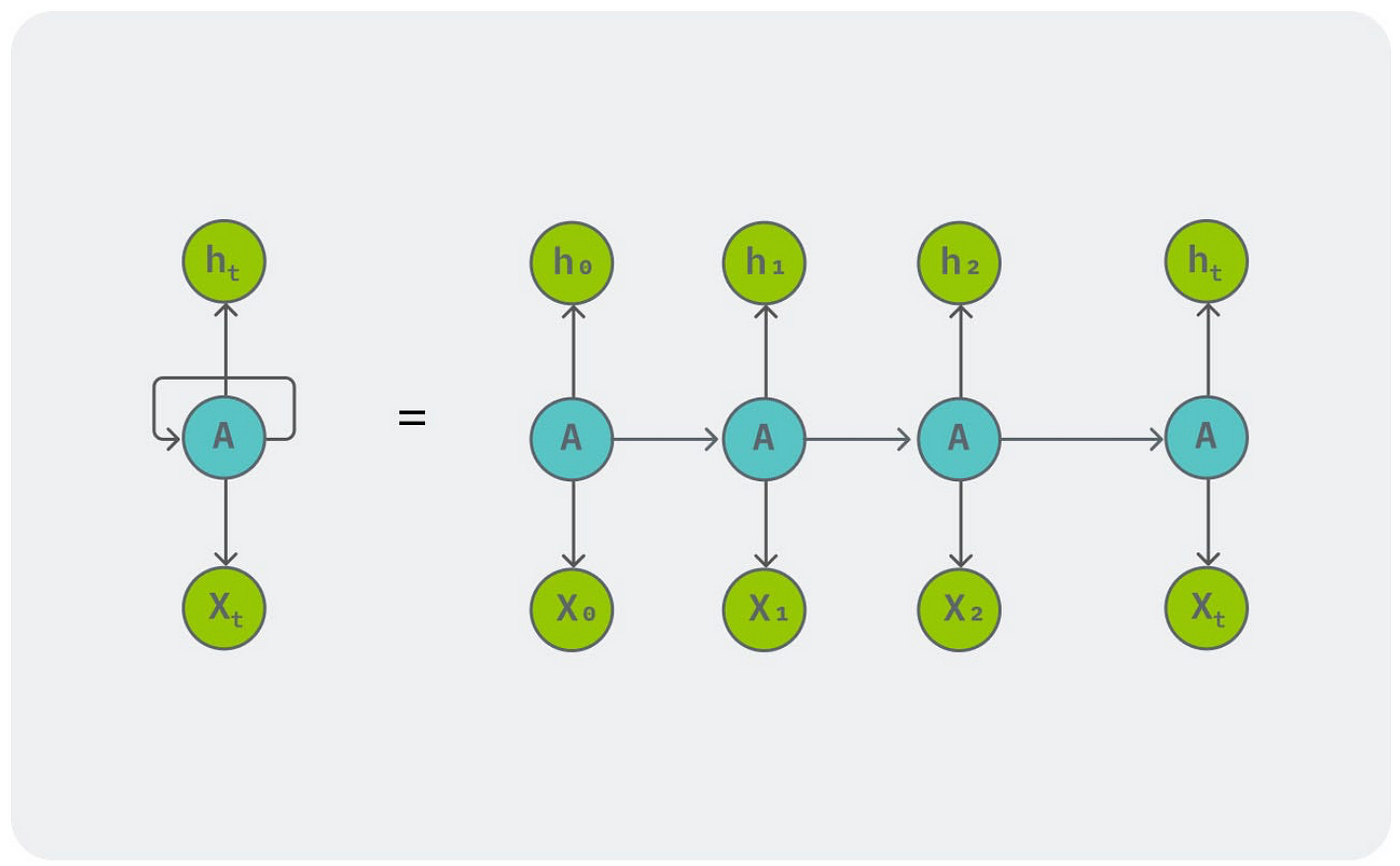
We split the sequence into single items (X₀) and pass it to RNN along with the initial state usually made up of only zeros and the model produces an output (h₀). This happens at the first time step. In the second time step we take the hidden input from the first and the next token X₁ to get h₁. So if we have n tokens then we need n time steps to map a sequence input to sequence output. This works fine for a lot of tasks but has some problems.
While effective for many tasks, RNNs had limitations, particularly with capturing long-range dependencies due to vanishing and exploding gradients. Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs) improved on this but still struggled with efficiency and scalability, especially for long sequences.
1. Slow Computation for Long Sequences: Processing each token sequentially involves a for-loop that runs for every token, making it a time-consuming process.
2. Vanishing or Exploding Gradients: During training, PyTorch calculates the derivative of the loss function with respect to the weights using the chain rule. As the number of hidden layers increases, the chain becomes longer, leading to derivatives that can either be extremely large or extremely small. This is problematic because CPUs and GPUs have limited precision for representing numbers. Consequently, the gradients can either vanish or explode, causing very small or very large updates to the model parameters, which is undesirable.
3. Difficulty in Accessing Information from Earlier in the Sequence: Due to the long chain of dependencies, the influence of the hidden state from the initial tokens diminishes as the sequence progresses. This means the effect of the first token on the last token becomes negligible, making it hard for the model to retain long-range dependencies.
Transformer solves all the above problems. The structure of the transformer can be divided into two macro blocks, the left part is called encoder and the right one is called decoder.
Paper :- Attention is all you need
We will look at each blocks on the encoder.
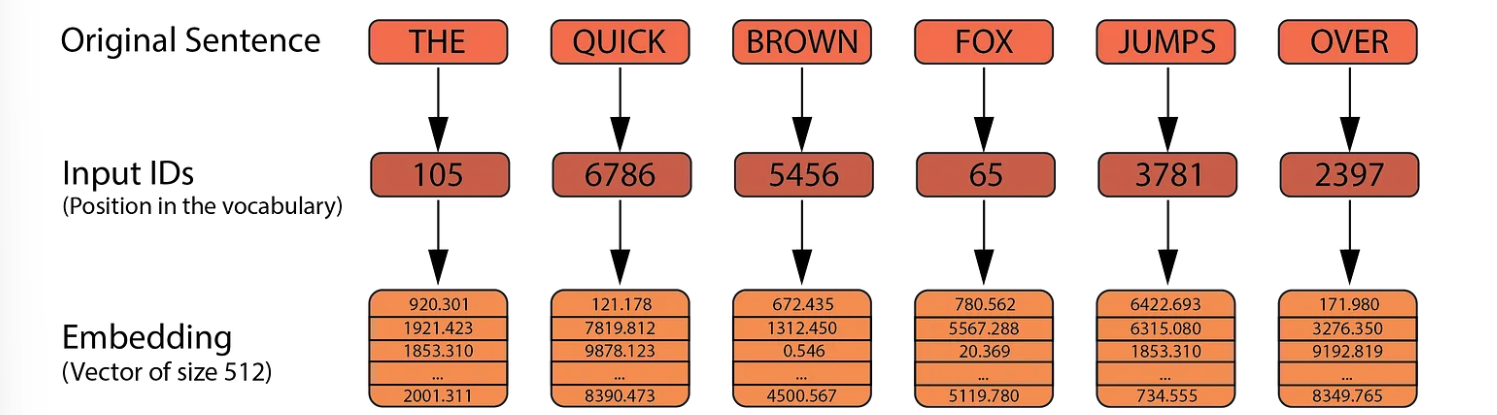
The encoder begins with the input embeddings. Given a sentence of six words, “The quick brown fox jumps over” we first transform the sentence into tokens. These tokens are then mapped to numbers that represent their positions in the vocabulary, known as Input IDs. These Input IDs are converted into vectors of size 512, referred to as embeddings. These embeddings are not fixed; they are parameters that the model learns and adjusts to capture the meaning of each word.
Note that while the Input IDs remain constant, the embeddings will change throughout the training process.
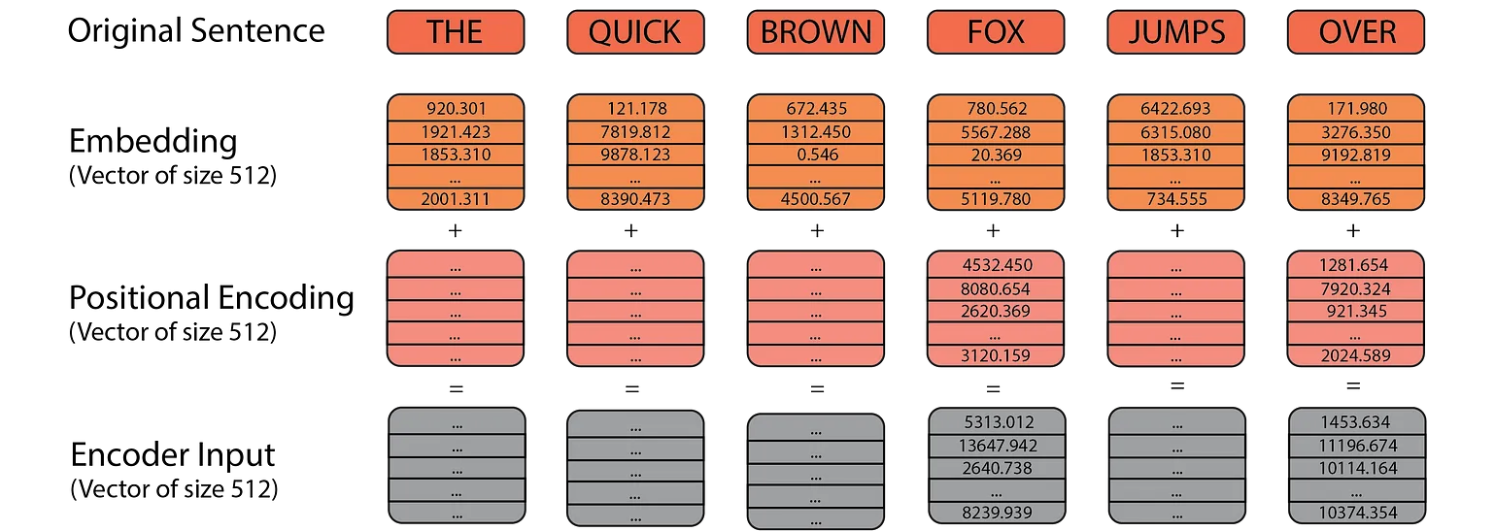
Next, we have the positional encoding. While our word embeddings capture the meaning of the words, they don’t convey any information about the position of each word in the sentence. We want the model to understand that words appearing close together in a sentence are related, and those far apart are less so. Positional encoding provides spatial information about each word’s position, helping the model recognize patterns in the sentence structure.
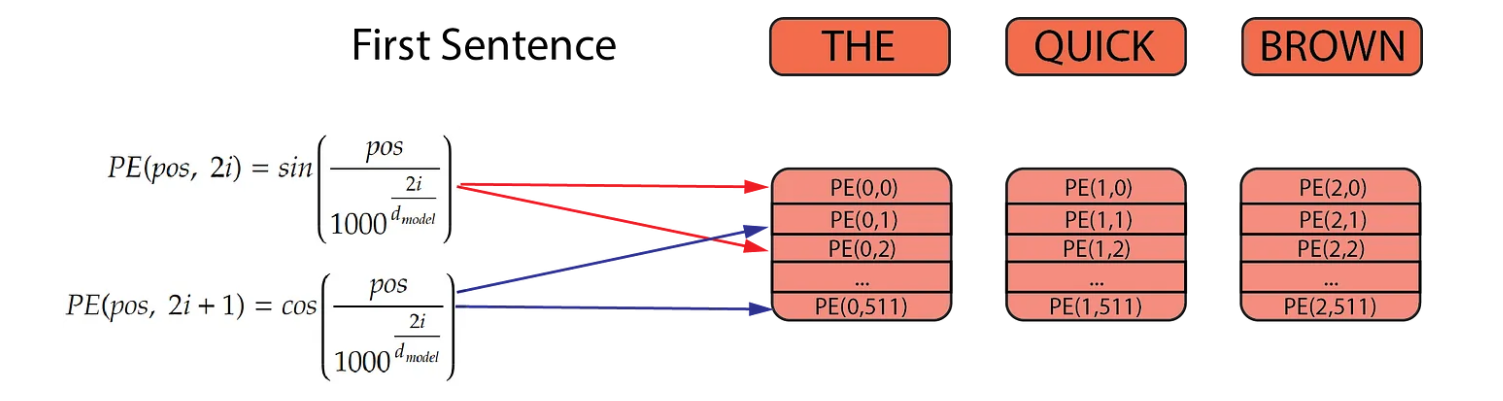
To calculate the positional encodings, we use two formulas as described in the original Transformer paper. The first formula is applied to even positions and the second to odd positions. These positional encodings are computed once and then reused during both training and inference for every sentence.
First, let’s understand what self-attention is. This mechanism existed before the Transformer, but the creators of the Transformer adapted it into multi-head attention. Self-attention allows the model to relate words to one another. The input embeddings capture the meanings of the words, while the positional encoding provides information about the position of each word in the sentence. The input matrix (6,512) is used three times here, for Q(query), K(key) and V(values). Using the formula mentioned in the paper, we will multiply Q (6,512) with Kᵀ (512,6) then divide it with √dₖ and then apply softmax.
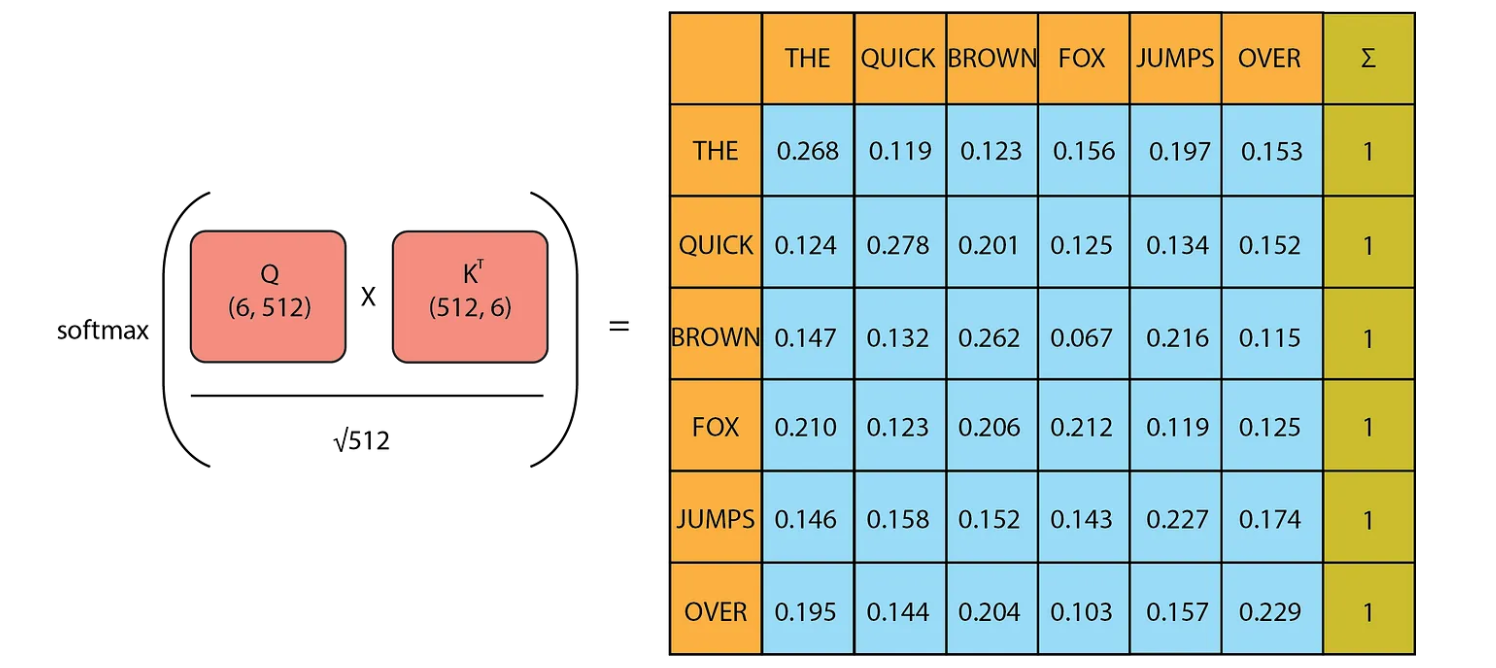
These values are a score, representing how intense the relationship between one word and another is.
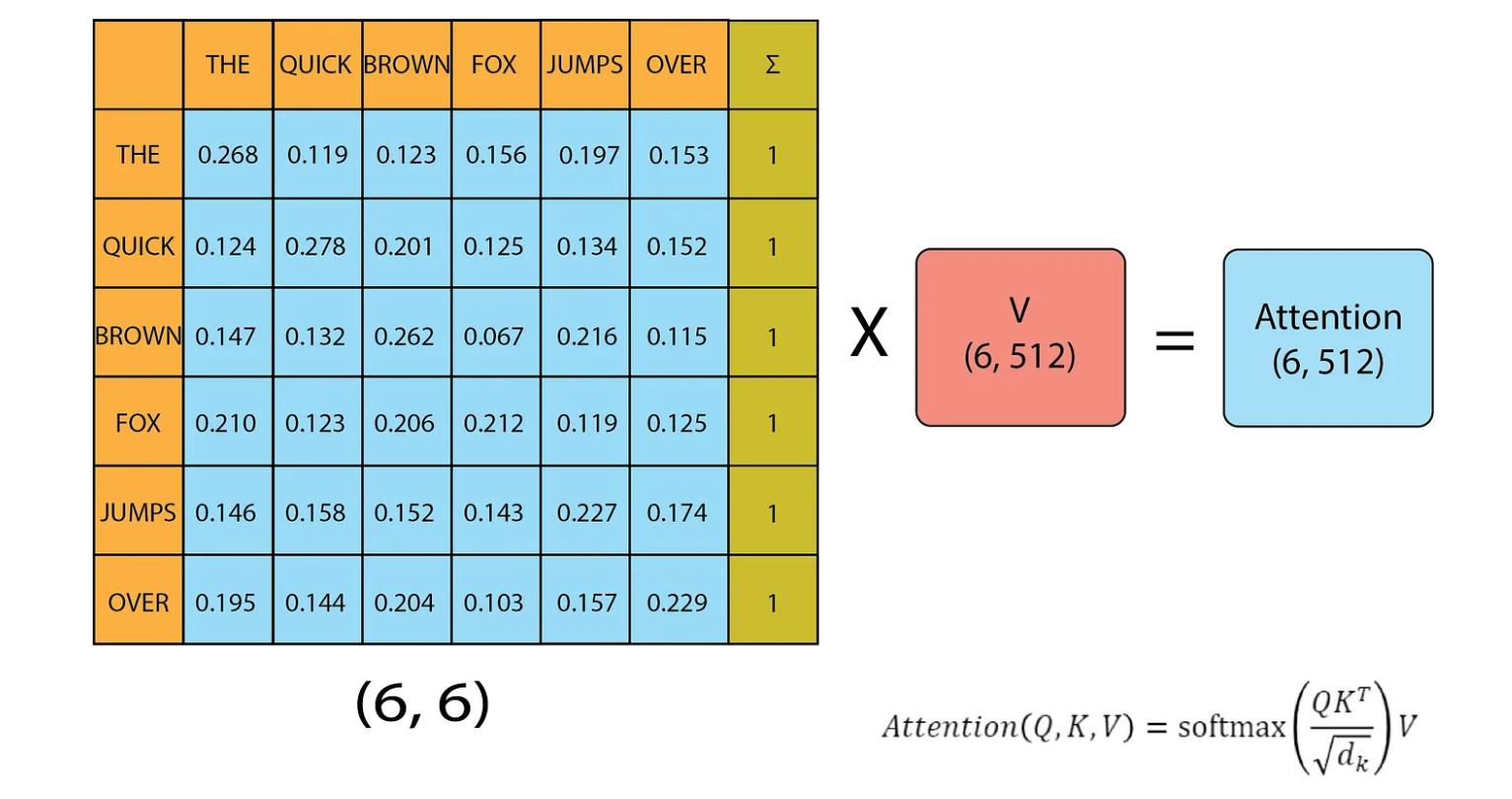
Finally we multiply this matrix with V to get the attention matrix. The dimension of the attention matrix is the same as the dimension of the initial matrix. After this the matrix embedding represents not only meaning and position of the word but also its relation with other words.
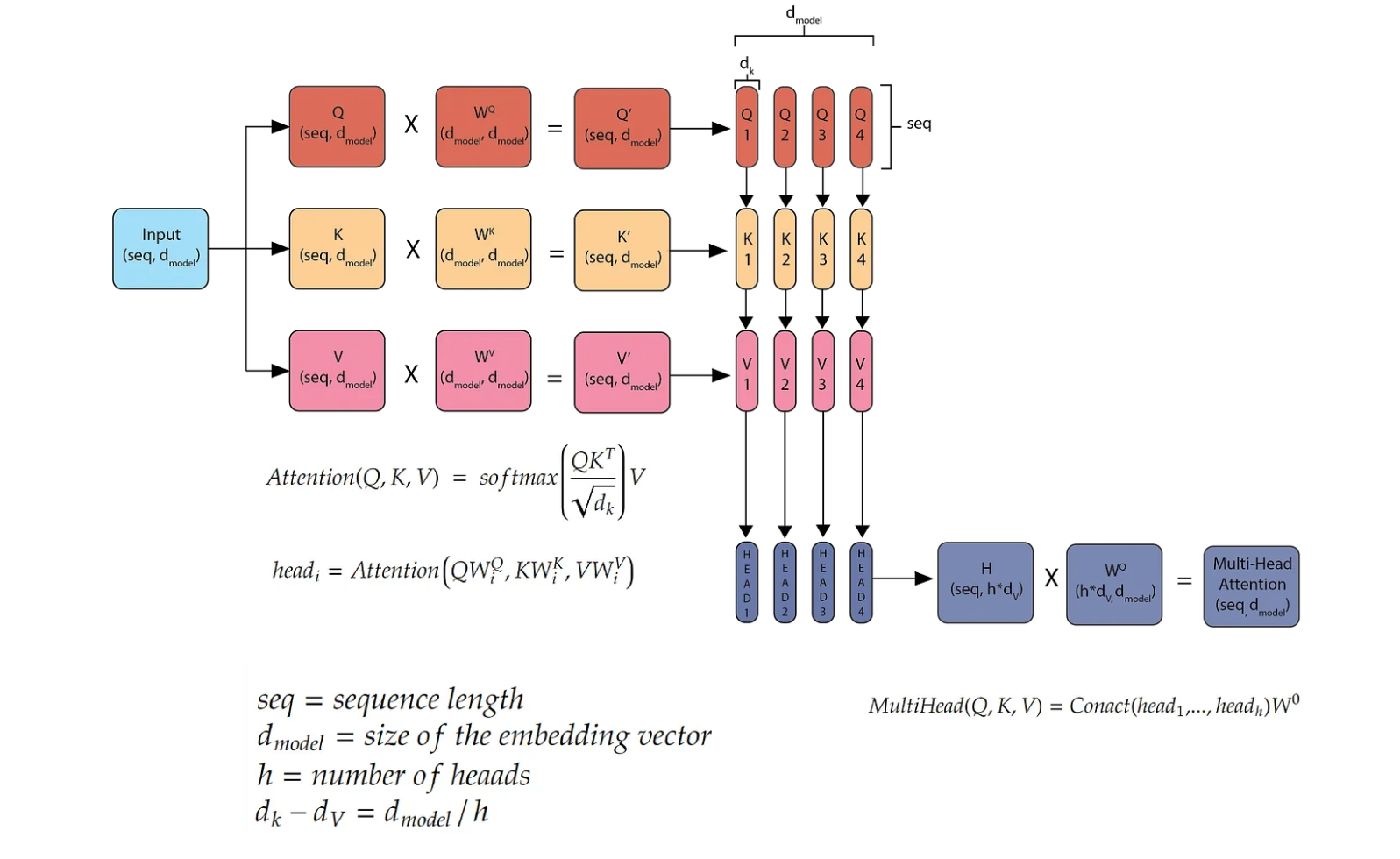
In multi-head attention, the input embeddings is duplicated to make three copies of it (Q, K, V) with dimension (seq, d_model) and each multiplied by parameter matrices (Wꟴ, Wᴷ, Wⱽ) with dimension (d_model, d_model). We get the resultant matrices (Q’, K’, V’) with dimension (seq, d_model). Next we will split these matrices by the d_model dimension. dₖ = d_model/h where h is the number of heads here equal to 4. We can then find the attention using the formula given in the paper. And we get small matrices head1, head2, head3 and head4 with dimension (seq, dᵥ) here dᵥ= dₖ. Then we will concatenate these matrices along the dᵥ dimension. Then we multiply this new matrix with weight matrix (h*dᵥ, d_model) to get the final output of multi-head attention (seq, d_model).
So instead of calculating the attentions on (Q’, K’, V’) we split them into multiple heads and calculate the attentions between these smaller matrices. Each head is watching a different aspect of the same word. For example in context a word can be a noun, a verb or an adverb. So head1 learns to relate the word as a noun, head2 learns to relate it as a verb and so on.
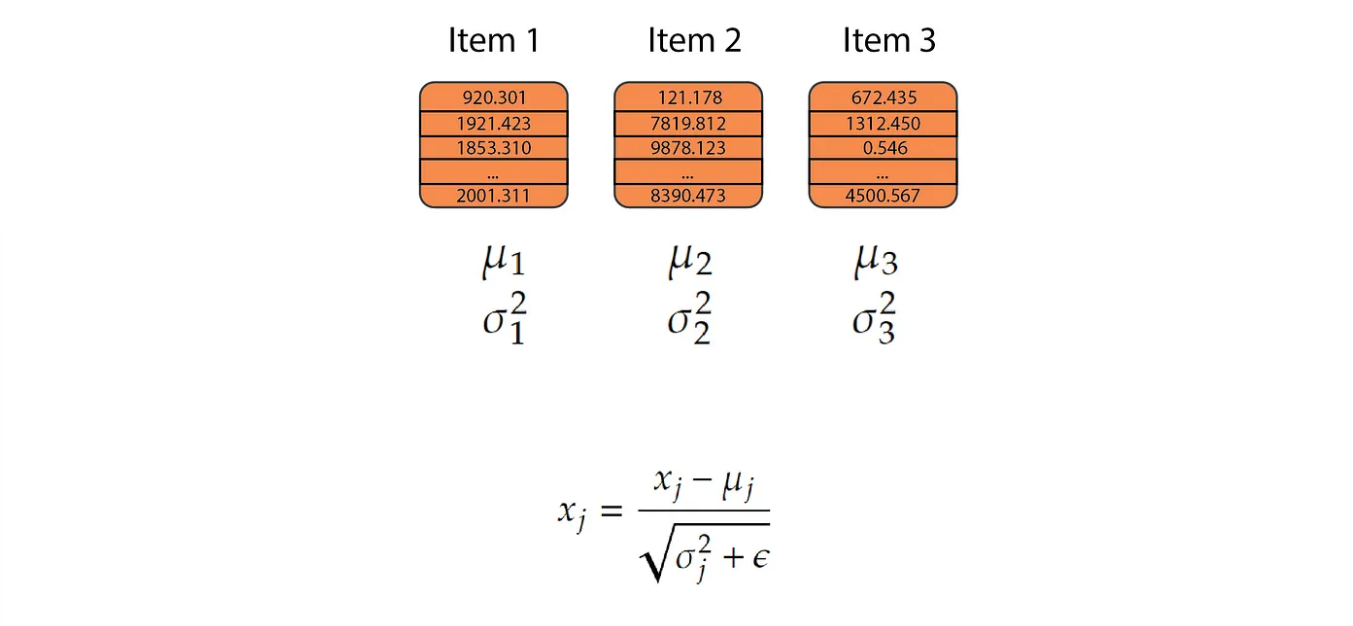
Suppose we have a batch of n items and each of them will have some features it could be an embedding. We will calculate the mean and variance of each of these items independently from each other and we replace each value with another value given by the expression. We multiply this with parameters 𝜶 or 𝛾(multiplicative) and 𝛽(additive). We also add 𝜖 for numerical stability so that the denominator value doesn’t approach zero.
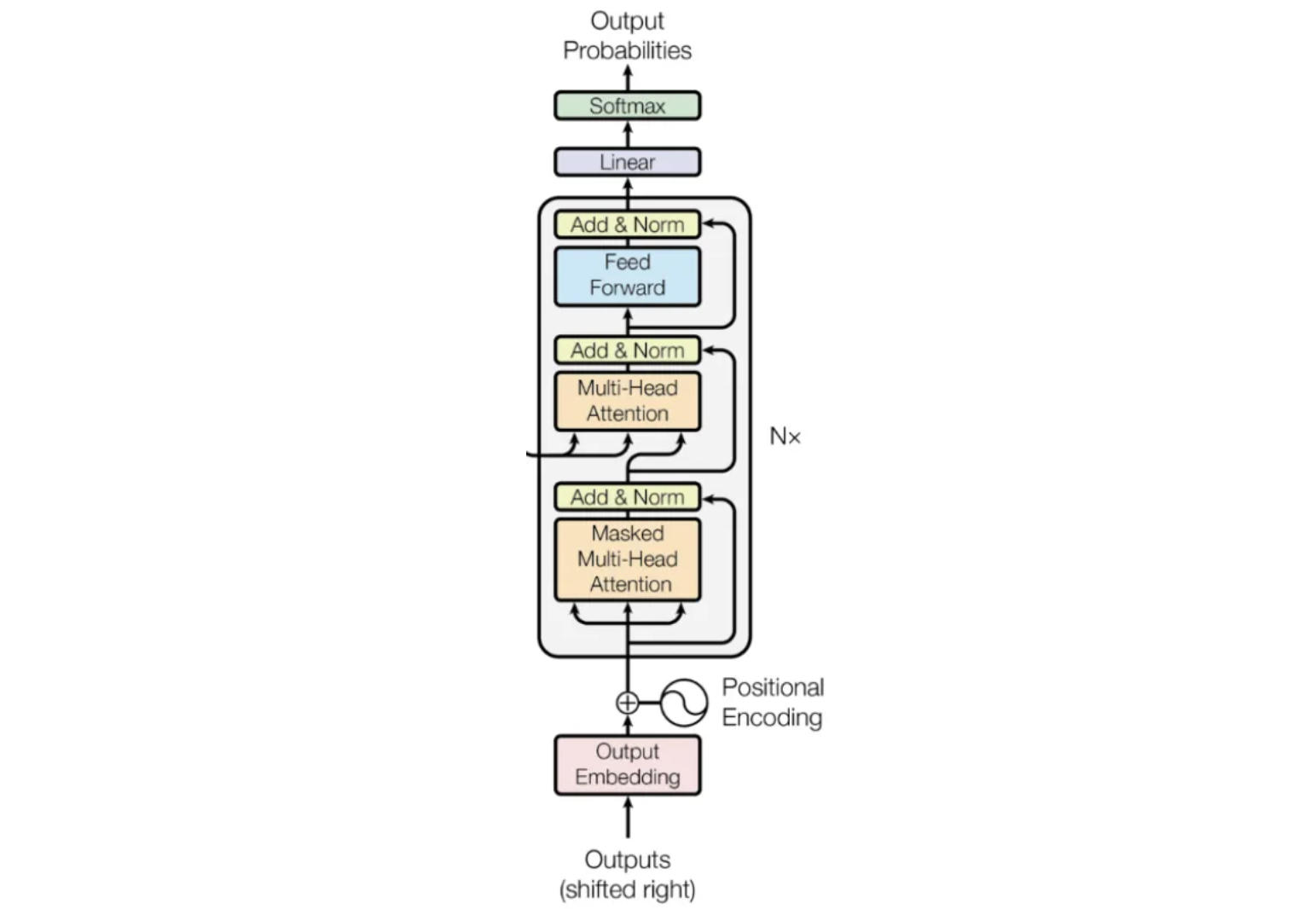
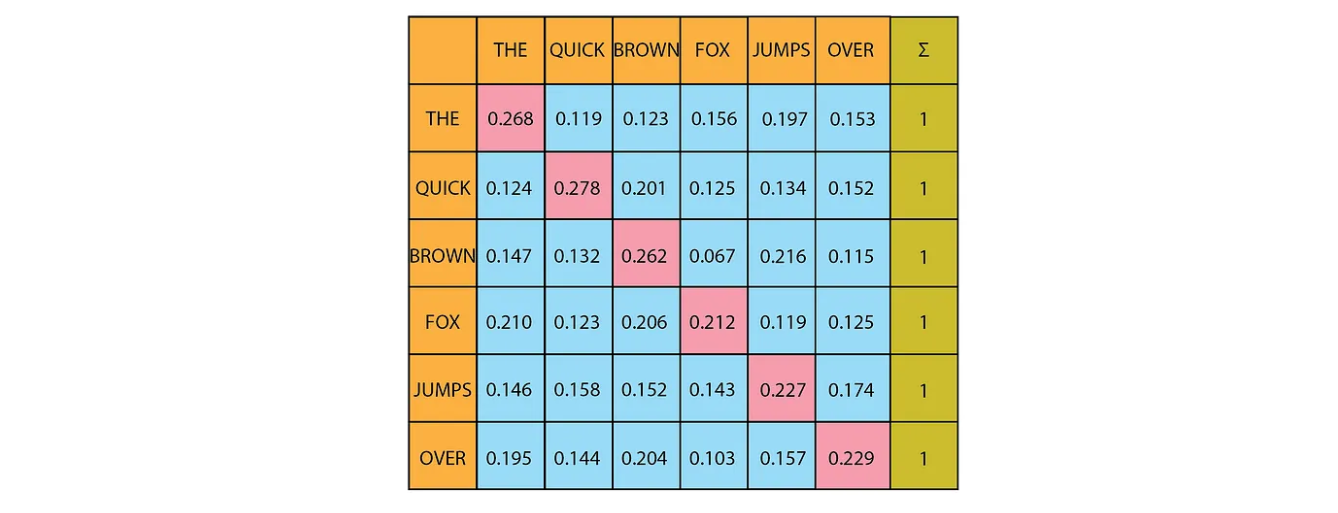
To ensure the model is causal, meaning that the output at a given position depends only on the words in the preceding positions, we need to prevent it from seeing future words. In multi-head attention, we achieve this by masking. Specifically, we replace all values above the main diagonal with negative infinity before applying the softmax function.
Output of the encoder are keys and values which go inside the decoder’s multi-head attention. This is cross self-attention as two parameters are the output of the encoder and the query matrix comes from the decoder’s input after processing through masked multi-head attention.
Linear Transformation: The input to the feedforward block is a tensor with shape (batch_size, seq, d_model). This tensor is passed through a fully connected linear layer, which transforms it to another tensor with shape (batch_size, seq, d_ff), where d_ff is the dimensionality of the feedforward layer, typically larger than d_model.
ReLU Activation: The output of the first linear layer is then passed through a rectified linear unit (ReLU) activation function element-wise. This introduces non-linearity into the model.
Second Linear Transformation: The result of the ReLU activation is passed through another linear layer, which projects the tensor back to the original dimensionality, (batch_size, seq, d_model).
The feedforward block allows the model to learn complex, non-linear transformations of the input. It is applied independently to each position in the sequence, making it highly parallelizable and efficient for processing sequences.
Suppose we are performing a language translation from English to French. We begin by taking the English sentence and sending it to the encoder. We add two special tokens: one at the beginning to mark the start of the sentence and another at the end to mark its conclusion. These tokens, taken from the vocabulary, indicate the boundaries of the sentence to the model.
Next, we convert the sentence into input embeddings, add positional encodings, and pass it through the encoder. The encoder produces an output matrix with the shape (seq, d_model). This matrix contains embeddings that capture the meaning of each word, its position, and its relationship with every other word in the sentence.
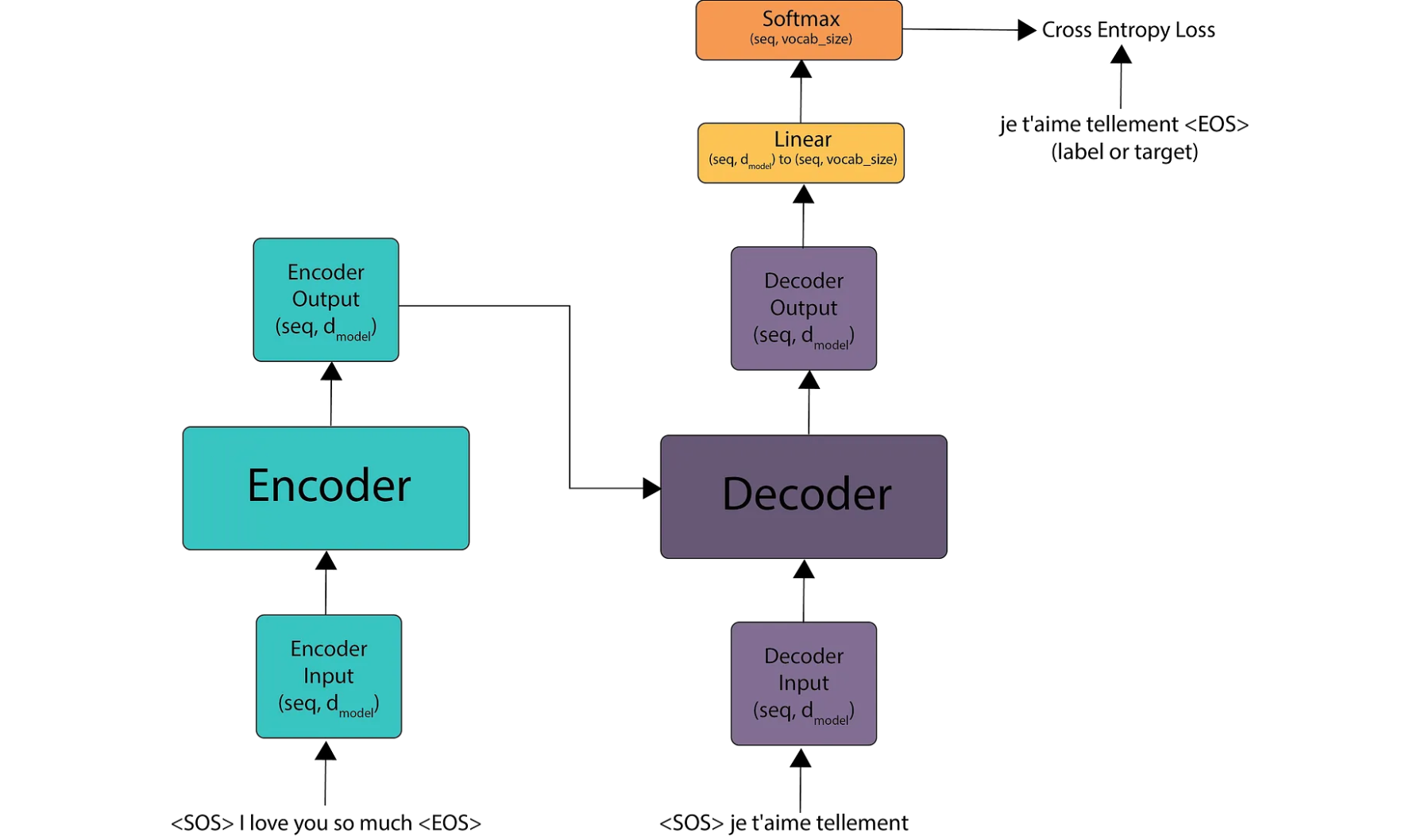
To convert an English sentence (“I love you so much”) into French (“je t’aime tellement”) using the Transformer model, we start by passing the start token (SOS) to the decoder. The output (shifted right) is then processed by converting it into embeddings, adding positional encoding, and feeding it into the decoder’s masked multi-head attention. Next, we take the output from the encoder as the query and keys, and the output from the masked multi-head attention as the values. These three components are then passed as input to the decoder’s multi-head attention.
The decoder produces an output matrix of shape (seq, d_model). To map this output to the vocabulary, we use a linear layer that transforms the matrix from (seq, d_model) to (seq, vocab_size). This linear layer helps determine the position of each word in the vocabulary, allowing us to understand the actual token output by the model. Finally, we apply a softmax function to generate probabilities for each token, producing the predicted French sentence.
The model’s output is compared to the target French sentence to calculate the loss. This loss is then used to update the model’s weights through backpropagation. This entire process occurs in a single time step.
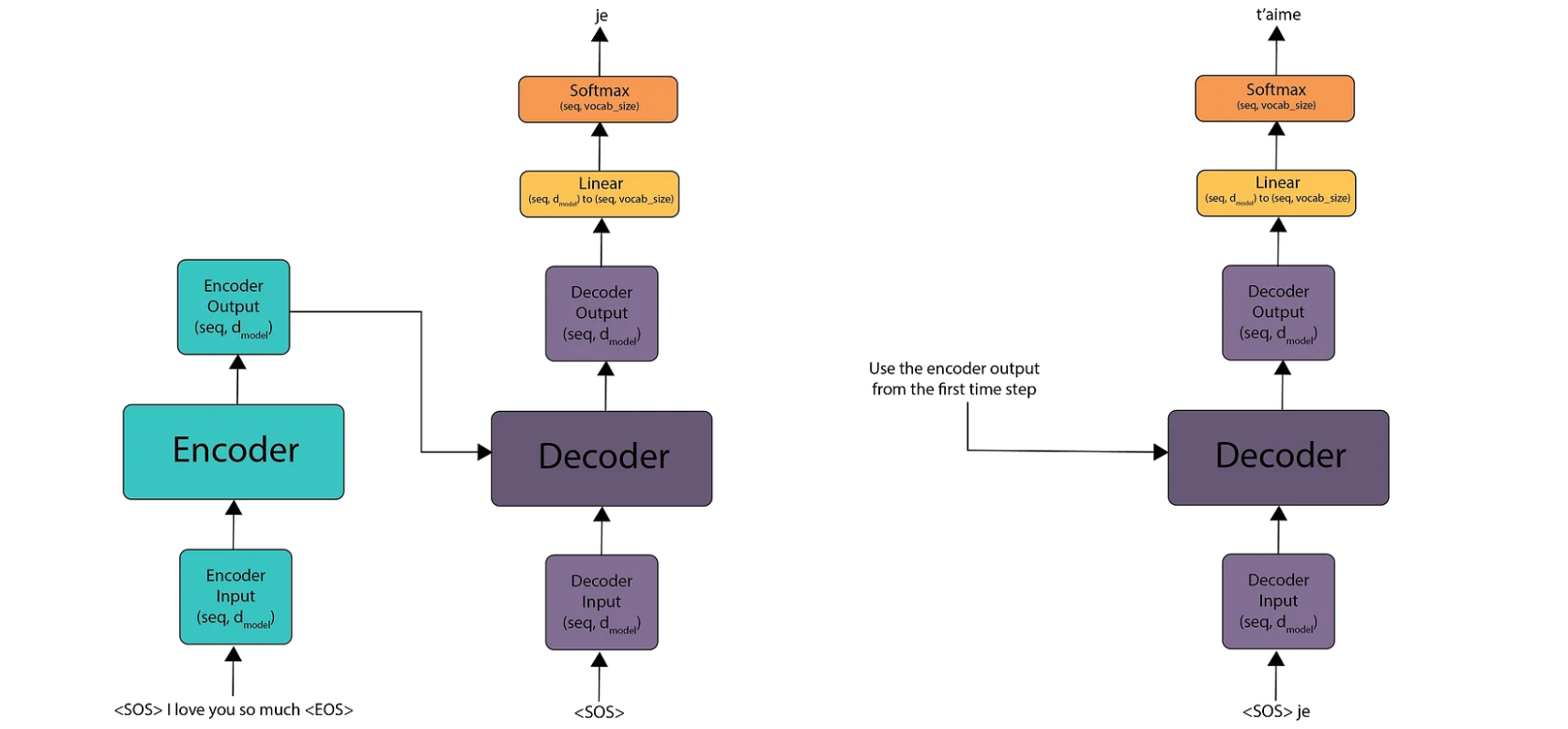
We start by passing the start-of-sentence (SOS) and end-of-sentence (EOS) tokens through the encoder, which produces an output matrix. For the decoder, we initially pass only the SOS token. The decoder’s output is then fed into a linear layer, producing logits. After applying the softmax function, we select the token from the vocabulary that corresponds to the highest value. This gives us the first token of the translated sentence, all occurring at time step 1.
At time step 2, we do not need to recompute the encoder’s output because the English sentence remains unchanged. Instead, we take the first French word predicted in the previous time step, append it to the decoder’s input, and feed it back into the decoder. This process is repeated to generate the second token. We continue this process until we encounter the EOS token.
In the decoding process, we traditionally selected the word with the highest softmax probability at each step. However, this greedy approach often does not yield optimal results.
A more effective strategy is Beam Search, where, at each decoding step, we consider the top B words based on their probabilities. We then evaluate all possible next words for each of these B words, keeping track of the top B most probable sequences. This strategy allows us to explore multiple potential sequences simultaneously, often leading to better overall performance in generating the output sequence.
The Transformer model has transformed natural language processing, especially in machine translation, with its self-attention mechanisms. It efficiently captures dependencies in input sequences, enabling accurate translations. In decoding, it selects the highest probability word at each step, though Beam Search, considering the top B words, often performs better. The Transformer’s ability to handle long-range dependencies and parallel processing makes it a significant advancement in NLP, with future developments promising further enhancements.
To gain a better intuition into the math behind each block :- Understanding Transformer with Math Examples
Next Article :- Build the Transformer Architecture from Scratch
