Introduction

Polynomial regression extends linear regression by modeling nonlinear relationships using polynomial terms. In this comprehensive guide, we'll implement polynomial regression from scratch, compare it with scikit-learn's implementation, and explore optimization techniques.

Mathematical Foundation

Linear Regression

Basic linear regression is expressed as:

where:

• y is the dependent variable
• x is the independent variable
• β₀ is the intercept
• β₁ is the slope
• ε is the error term

Polynomial Regression

Polynomial regression extends this to:

Cost Function

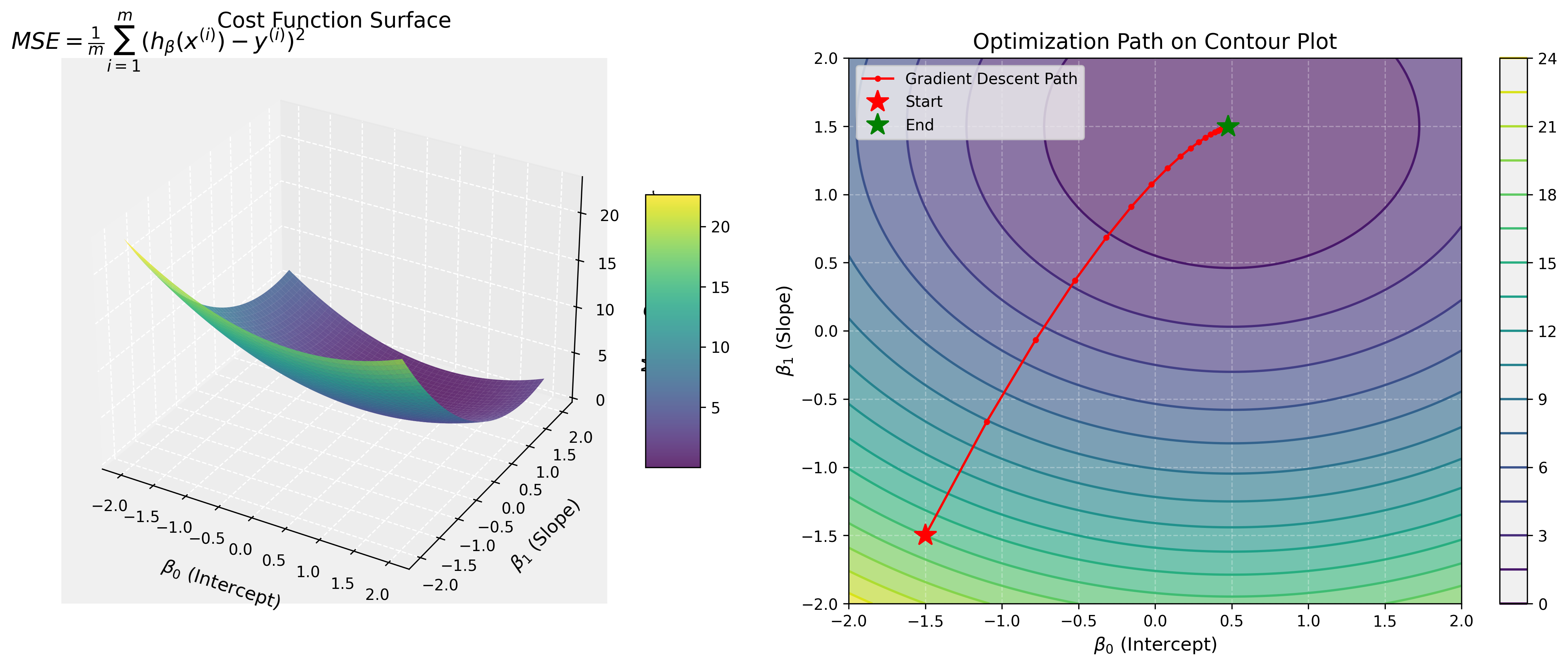
The Mean Squared Error (MSE) cost function:

Implementation Steps

1. Data Generation and Visualization

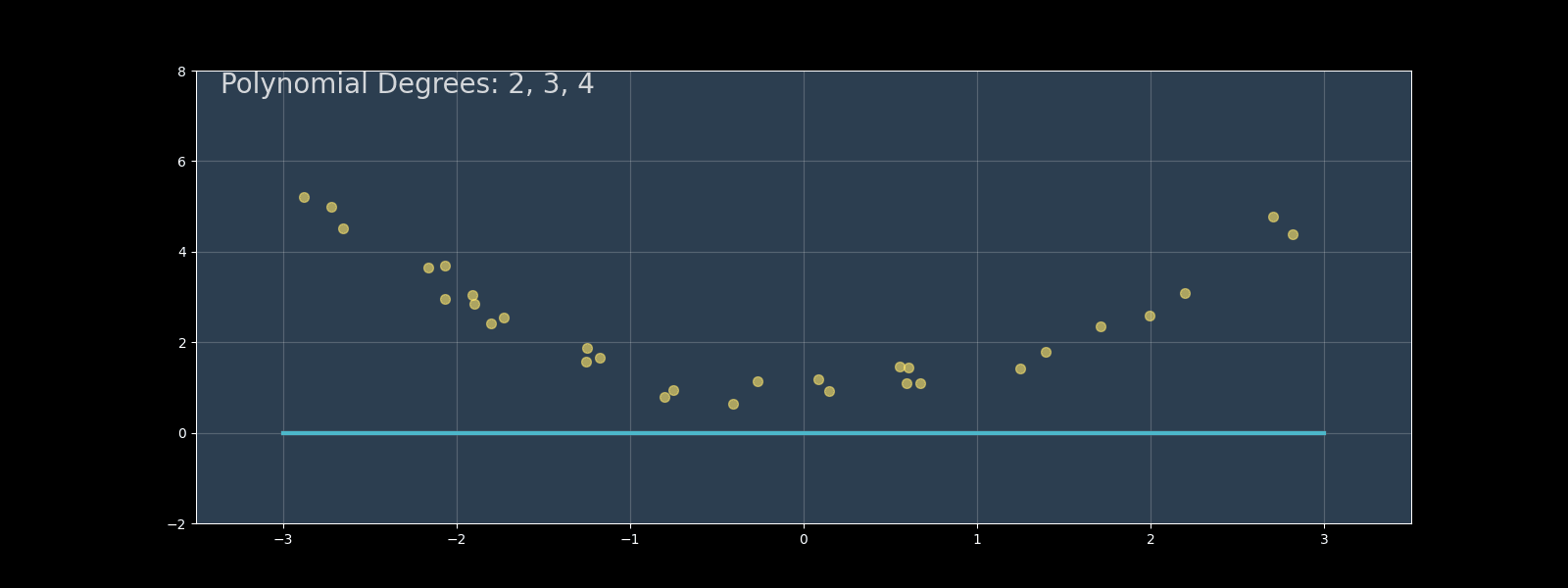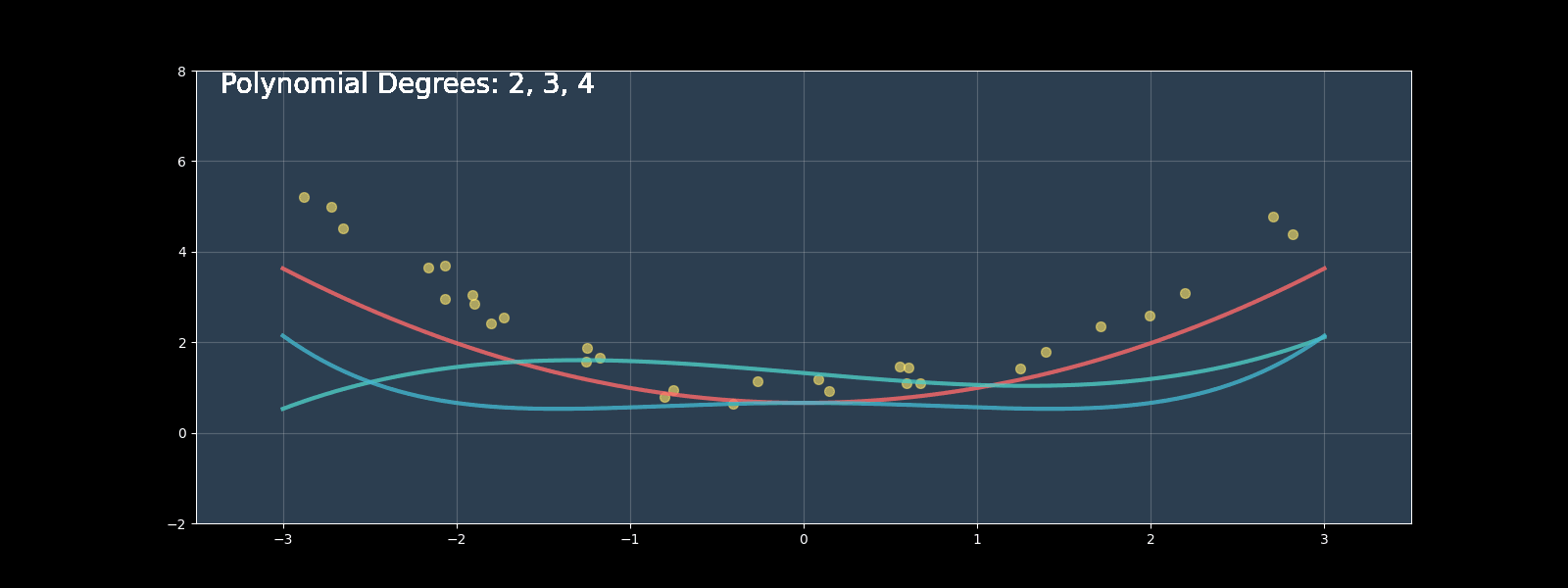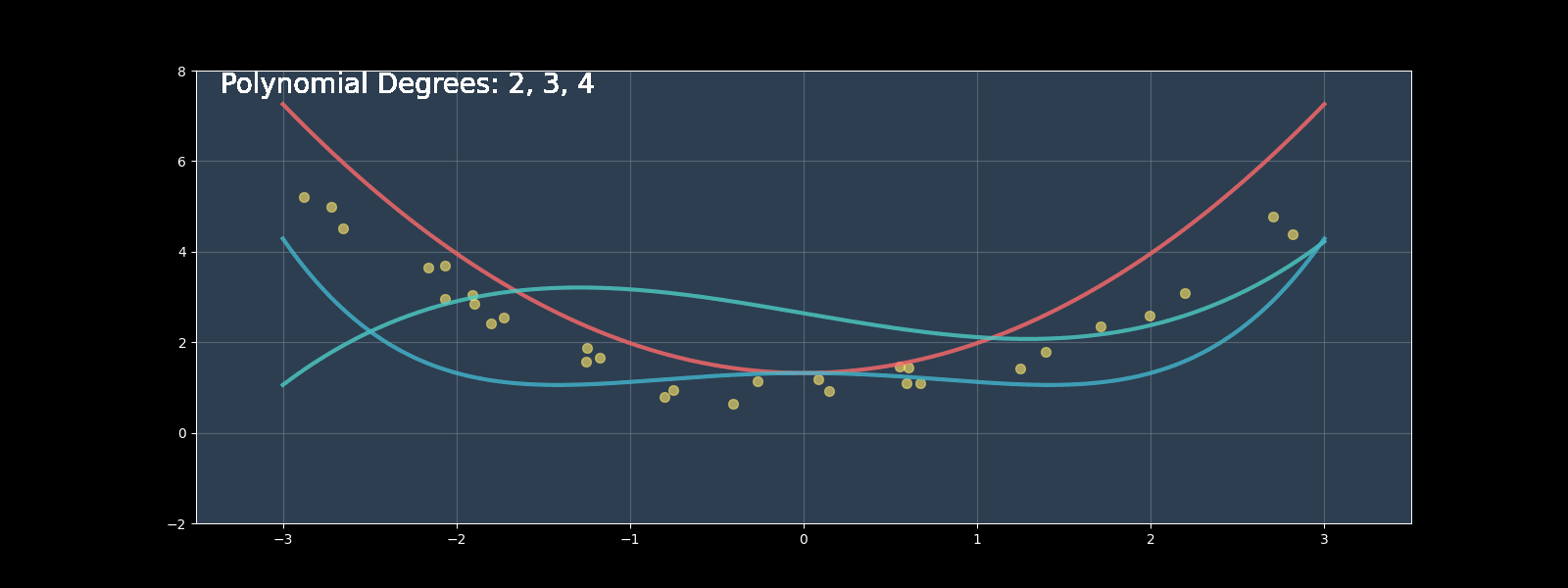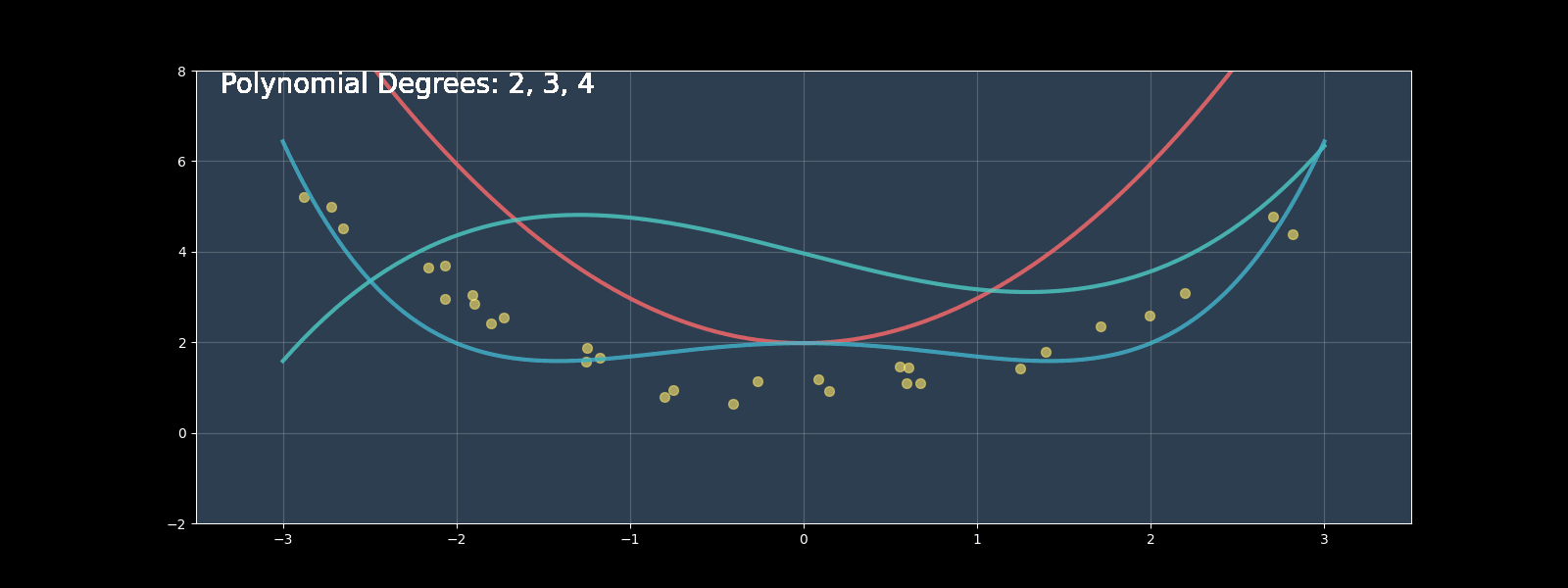
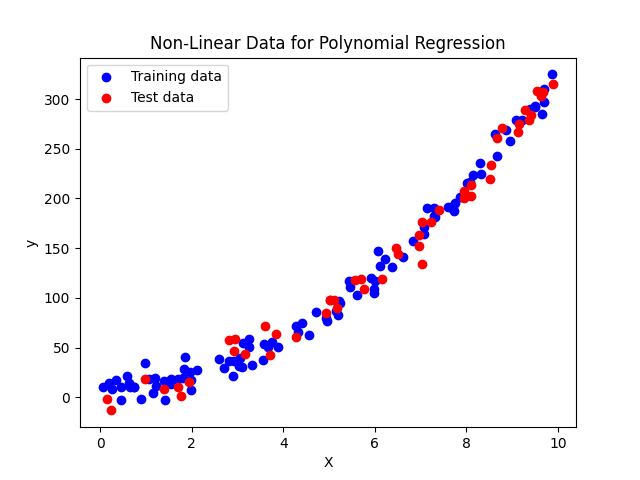
First, let's create synthetic nonlinear data:

import numpy as np
import matplotlib.pyplot as plt

# Create non-linear data (quadratic)
np.random.seed(42)
X_train = np.random.rand(100, 1) * 10
y_train = 3 * X_train**2 + 2 * X_train + 5 + np.random.randn(100, 1) * 10

X_test = np.random.rand(50, 1) * 10
y_test = 3 * X_test**2 + 2 * X_test + 5 + np.random.randn(50, 1) * 10

2. Custom Polynomial Regression Implementation

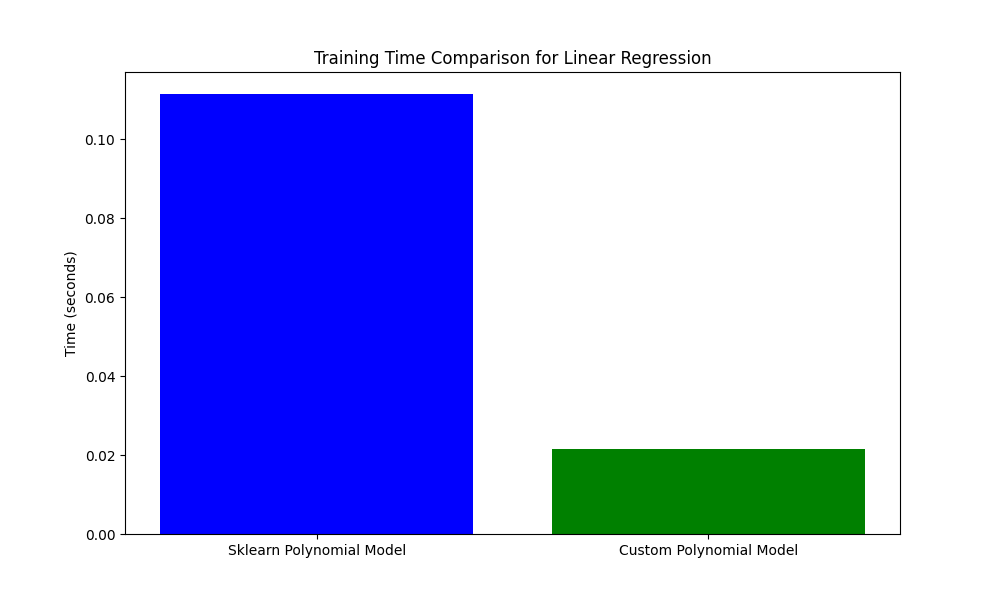
Our enhanced CustomPolynomialEstimator class:

class CustomPolynomialEstimator:
    def __init__(self, degree=2, include_bias=True, include_interactions=True, 
                 feature_selection_threshold=0.01, use_scaling=True):
        self.degree = degree
        self.include_bias = include_bias
        self.include_interactions = include_interactions
        self.feature_selection_threshold = feature_selection_threshold
        self.use_scaling = use_scaling
        self.scaler = StandardScaler() if use_scaling else None

Key Features:

1. Feature Scaling: Normalizes features using StandardScaler
2. Polynomial Transformation: Creates polynomial terms up to specified degree
3. Interaction Terms: Optional interaction terms between features
4. Feature Selection: Variance-based feature selection
5. Memory Optimization: Efficient matrix operations

3. Model Comparison

Build-In Linear Regression VS Build-In Polynomial Regression

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

model_sklearn = make_pipeline(
    PolynomialFeatures(degree=2), 
    LinearRegression()
)

Build-In Linear Regression VS Custom Polynomial Regression

import numpy as np
from itertools import combinations, combinations_with_replacement
from sklearn.preprocessing import StandardScaler
from sklearn.base import BaseEstimator, RegressorMixin

class CustomPolynomialEstimator:
    def __init__(self, degree=2, include_bias=True, include_interactions=True, 
                 feature_selection_threshold=0.01, use_scaling=True):
        self.degree = degree
        self.include_bias = include_bias
        self.include_interactions = include_interactions
        self.feature_selection_threshold = feature_selection_threshold
        self.use_scaling = use_scaling
        self.scaler = StandardScaler() if use_scaling else None
        self.feature_importances_ = None

model_custom = make_pipeline(CustomPolynomialEstimator(degree=2, include_interactions=True), LinearRegression())
model_custom.fit(X_train, y_train)

pred_custom = model_custom.predict(X_test)

Performance Metrics

4. Gradient Descent Implementation

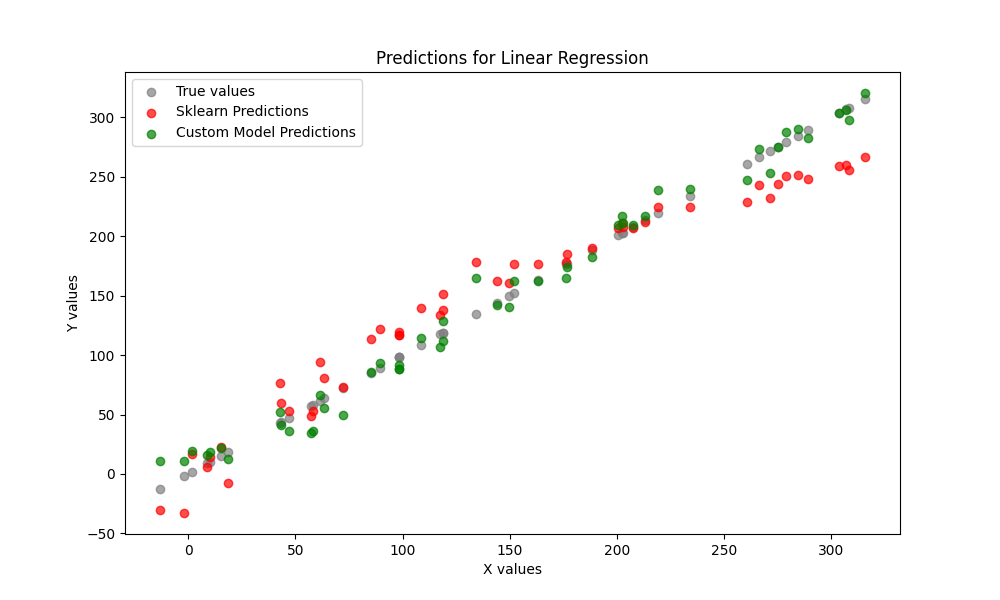
The gradient descent update rule:

where α is the learning rate.

Build-In Gradient Descent VS Build-In Polynomial Regressor

from sklearn.linear_model import SGDRegressor

sgd_model = make_pipeline(
    PolynomialFeatures(degree=2),
    SGDRegressor(max_iter=1000, tol=1e-3)
)

Build-In Gradient Descent VS Custom Polynomial Regressor

custom_sgd = make_pipeline(CustomPolynomialEstimator(degree=2, include_interactions=True), SGDRegressor())

# Measure training time
start_time = time.time()
custom_sgd.fit(X_train, y_train)
pred_custom_sgd = custom_sgd.predict(X_test)

# Calculate R^2 score
score_custom_sgd_train = custom_sgd.score(X_test, y_test)
print(f"Custom SGD Model Training R^2 Score: {score_custom_sgd_train:.4f}")

end_time = time.time()
time_custom_sgd = end_time - start_time

print(f"Time taken for training and prediction: {time_custom_sgd:.4f} seconds")

Performance Metrics for Gradient Descent

Results Analysis

1. Model Performance

Optimization Techniques

1. Feature Selection

2. Regularization

• L1 (Lasso):

• L2 (Ridge):

Code Repository

Complete implementation: GitHub Repository Link

Future Improvements

1. Cross-validation implementation
2. Advanced regularization techniques
3. Sparse matrix support
4. GPU acceleration

References

1. Scikit-learn Documentation
2. Statistical Learning Theory
3. Numerical Optimization Techniques

---

Follow me on social media:

• LinkedIn
• NoteBook
• GitHub