"Bagging Predictors : " by Leo Breiman, published in Machine Learning, 24, 123-140 (1996), discusses a method called "Bagging" (Bootstrap Aggregating), which was designed to improve the accuracy of predictors in both classification and regression tasks. The technique involves generating multiple versions of a predictor through bootstrap sampling, and then averaging the outputs (for numerical predictions) or voting (for classification tasks) to produce a final prediction. The paper provides a theoretical foundation, experimental results, and proofs demonstrating why and when bagging works effectively. Below is a detailed blog-style explanation of the key concepts, results, and proofs from the paper.

Introduction to Bagging

In machine learning, a predictor is trained on a learning set of data, , where represents either class labels or numerical responses, and represents feature vectors. The goal is to generate a function that predicts based on new, unseen feature vectors .

Breiman’s work introduces the concept of bagging as a method to enhance the accuracy of predictors. Bagging creates multiple versions of a predictor by drawing random bootstrap samples (with replacement) from the training set, and then averaging these models for numerical responses or aggregating their votes for classification. This reduces variance and mitigates overfitting, particularly for models that are inherently unstable, meaning their predictions are sensitive to small changes in the training data.

Key Concept: Bootstrap Aggregating (Bagging)

Bagging involves the following steps:

1. Bootstrap Sampling: Given a training set , generate bootstrap replicates, each denoted by , by sampling with replacement from . Each sample is of size , the number of observations in .
2. Train Predictors: Train a predictor on each bootstrap sample .
3. Aggregate Predictions:
   • For regression tasks (numerical outcomes), the final prediction is the average of the individual predictions:
   • For classification tasks, the final prediction is determined by a majority vote from all the predictors:

Why Bagging Works: Theoretical Foundation

Breiman provides a theoretical justification for why bagging can improve predictive accuracy. The key lies in understanding how the instability of a model contributes to its performance.

• Instability refers to how much a model changes when trained on slightly different datasets. For instance, models like decision trees or neural networks are known to be unstable—small changes in the training data can lead to significant changes in the output predictor.

• Variance Reduction: Bagging reduces the variance of a predictor without increasing the bias. The final aggregated predictor is less sensitive to fluctuations in the training set, which typically arise from model instability. This stabilization improves accuracy, especially in high-variance models.

To illustrate why bagging reduces variance in regression, consider the expected error of a predictor:

The bagged predictor, being an average of many bootstrapped models, will have lower variance compared to a single model, as averaging reduces the effect of outliers or overfitting to noise in the training data.

For classification, the improvement stems from a better approximation of the Bayes optimal classifier. Aggregating the votes from unstable models leads to better generalization and, in many cases, a higher accuracy compared to using a single model.

.

Theoretical Proofs

Breiman provides theoretical support for bagging’s effectiveness through the following key proofs:

1. Reduction in Mean Squared Error (MSE) for Regression

The section provided from the paper "Bagging Predictors" by Leo Breiman details a proof for the effectiveness of bagging in numerical prediction scenarios. Let's break down this proof for a clearer understanding:

Setup and Notation

The paper establishes that each data pair is drawn independently from a probability distribution . Here, is a numerical output, is the input, and is the predictor trained on the dataset . The aggregated predictor, denoted as , is then the expected value over of , i.e.,

Proof of Reduction in MSE

Breiman then discusses that for a fixed input and output , the error term can be expressed as:

He then utilizes the fact that and applies the inequality to the third term, leading to:

Integrating this inequality over the joint distribution of and yields that the mean-squared error of is less than the mean-squared error averaged over of .

Instability and Bagging

The paper highlights that the improvement from bagging hinges on the instability of the predictor. If changes in the dataset lead to significant variations in , bagging can substantially reduce prediction error through averaging, as unstable models exhibit large variances that are averaged out.

Practical Implications

Bagging leads to a predictor , which not only depends on but also on a bootstrap approximation to the probability distribution . concentrates the probability mass uniformly over the observed data points, creating a new distribution from which the bootstrap samples are drawn. Breiman notes that while bagging improves performance through averaging, its effectiveness is contingent on the underlying instability of the model.

Stability vs. Instability

The paper concludes this section by discussing the limits of bagging:

• For stable procedures, where slight changes in do not significantly affect , bagging does not lead to improvement and might not reach the accuracy of for the original distribution .
• For unstable procedures, bagging can lead to significant improvements, but there is a "cross-over point" where further gains diminish as the procedure's predictions approach the theoretical limits of accuracy on that data.

This detailed proof from Breiman’s paper underscores the theoretical basis for bagging in reducing variance, especially in the context of unstable prediction methods, thereby improving the overall accuracy of numerical predictions.

Foundations for Classification

Definition of and :

• is the probability that the classifier predicts class for an input when trained on dataset .
• is the true probability of class given input .

Key Concepts

Probability of Correct Classification:
The probability that the predictor correctly classifies an input as class is computed as:

This sums over all possible classes , where acts as a weight for how frequently the model predicts class , and is the actual likelihood of being class .

Overall Accuracy:
The overall probability of correct classification across the input space is:

Here, is the probability distribution of over the input space.

Proof of Bagging's Effectiveness

Maximizing Correct Classification:
For any class probability , the sum:

holds, where equality is achieved if . This condition implies that the classifier is perfectly aligned with the true class probabilities.

Bayes Classifier:
The ideal classifier, known as the Bayes classifier, is:

which leads to the highest attainable correct classification rate:

Order-Correctness:
A classifier is "order-correct" at input if:

This means ranks the classes in the same order as their true probabilities. An "order-correct" classifier is not necessarily highly accurate but ensures that the most likely class according to is indeed the most probable class.

How Bagging Enhances Classification

Bagging tends to make an unstable classifier more robust by reducing variance through averaging predictions from multiple models. If is order-correct, bagging further enhances accuracy by transforming into a nearly optimal predictor, especially in cases where the base classifiers are good but not perfect. This is particularly useful when dealing with complex decision boundaries or datasets where the models exhibit significant variance in their predictions.

Limitations of Bagging

The proof also underscores that if the classifiers are stable, meaning that changes in do not significantly affect their predictions, then bagging will not improve performance and can even degrade it. This is due to the fact that bagging inherently relies on variance between the classifiers to improve accuracy.

Conclusion

Breiman’s paper on bagging predictors is a foundational work in ensemble methods, introducing a simple yet powerful technique for improving the accuracy of predictive models. By reducing variance and mitigating overfitting, bagging transforms unstable models into robust, high-performing predictors.

The results of the paper, both theoretical and empirical, demonstrate the wide applicability of bagging across different types of tasks, from classification to regression. While bagging may not always yield significant improvements for stable models, its simplicity and effectiveness for high-variance models have made it a cornerstone of modern machine learning.

Breiman concludes by discussing the practical aspects of bagging, such as the number of bootstrap replications required and the computational efficiency of the method, particularly in parallel computing environments.

In summary, bagging is a versatile and essential tool in the machine learning toolbox, particularly for models where variance is the dominant source of error.

Code

Lets take a look with a simple example of how bagging can be implemented in Python using the BaggingRegressor and BaggingClassifier classes from the sklearn.ensemble module.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor

# Generating synthetic data from a non-linear function
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.power(X, 2).ravel() / 10 + 0.1 * np.random.randn(*X.shape).ravel()

# Plotting settings
plt.figure(figsize=(16, 10))
x_plot = np.linspace(0, 5, 500).reshape(-1, 1)

# Train a different model with increasing number of weak learners
for i, n_estimators in enumerate([1, 2, 4, 8, 16, 32], start=1):
    # Bagging regressor
    bagging = BaggingRegressor(base_estimator=DecisionTreeRegressor(),
                               n_estimators=n_estimators,
                               random_state=0).fit(X, y)
    # Predictions
    y_pred = bagging.predict(x_plot)

    # Plot
    plt.subplot(2, 3, i)
    plt.scatter(X, y, c='k', label="training samples")
    plt.plot(x_plot, y_pred, c='r', label=f"n_estimators={n_estimators}", linewidth=2)
    plt.xlabel("Data")
    plt.ylabel("Target")
    plt.title(f"Bagging with {n_estimators} trees")
    plt.legend()

plt.tight_layout()
plt.show()

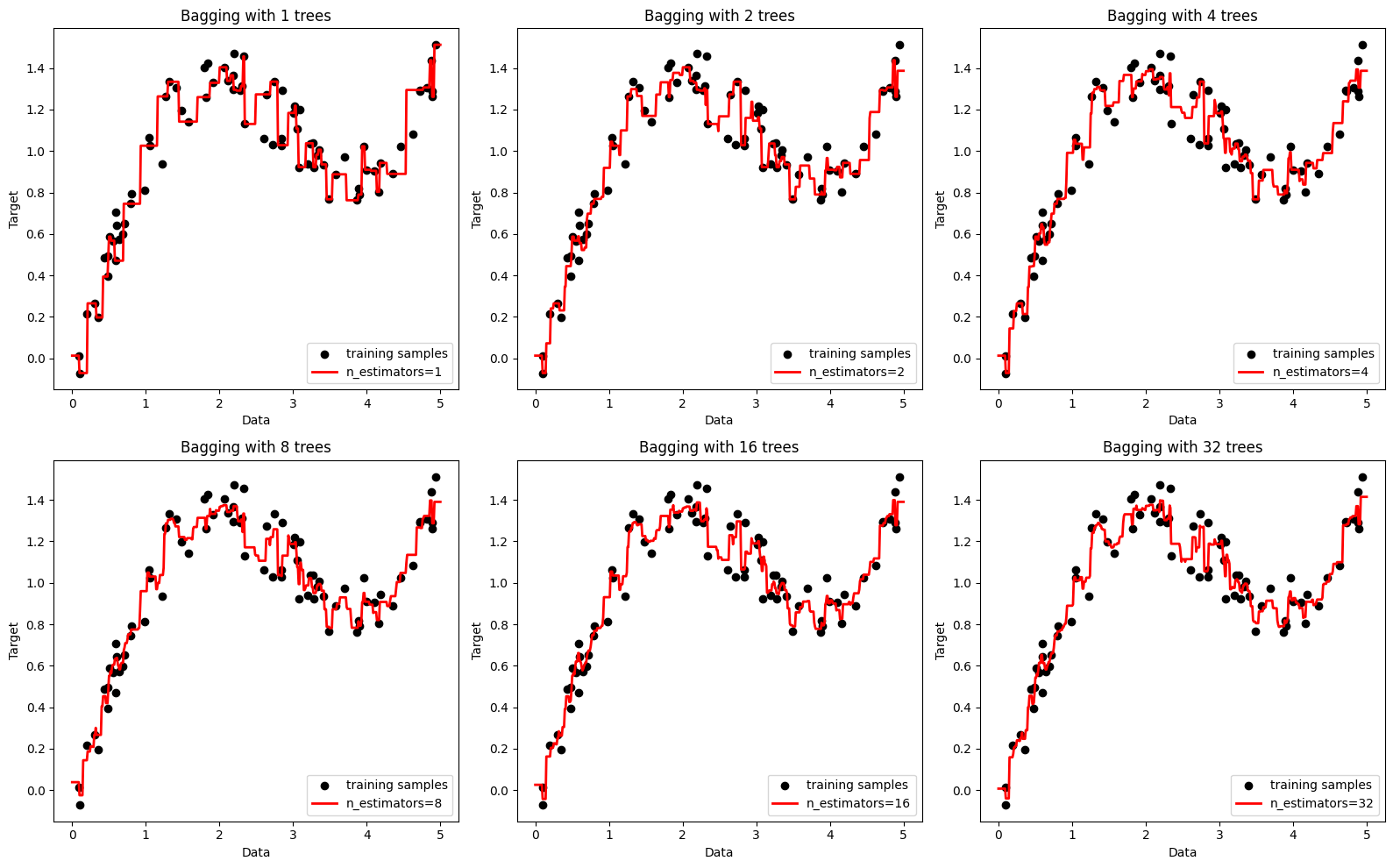
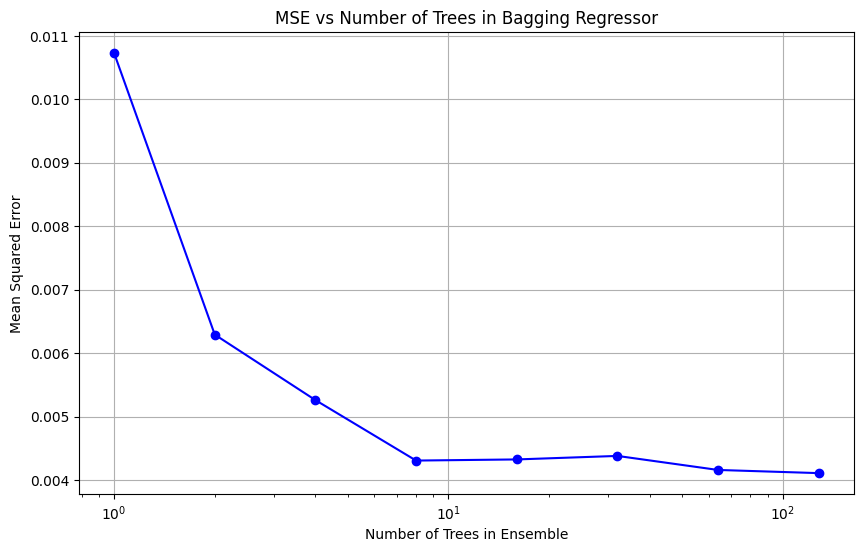
Lets take a look at the loss curve for the bagging regressor.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import mean_squared_error

# Generate synthetic data
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.power(X, 2).ravel() / 10 + 0.1 * np.random.randn(*X.shape).ravel()

# Test data for prediction and calculating MSE
X_test = np.linspace(0, 5, 500).reshape(-1, 1)
y_true = np.sin(X_test).ravel() + np.power(X_test, 2).ravel() / 10

# Number of trees in the ensemble
n_estimators_list = [1, 2, 4, 8, 16, 32, 64, 128]
mse_results = []

# Evaluate bagging ensemble with different numbers of trees
for n_estimators in n_estimators_list:
    bagging = BaggingRegressor(base_estimator=DecisionTreeRegressor(),
                               n_estimators=n_estimators,
                               random_state=0).fit(X, y)
    y_pred = bagging.predict(X_test)
    mse = mean_squared_error(y_true, y_pred)
    mse_results.append(mse)

# Plotting the results
plt.figure(figsize=(10, 6))
plt.plot(n_estimators_list, mse_results, marker='o', linestyle='-', color='b')
plt.xlabel('Number of Trees in Ensemble')
plt.ylabel('Mean Squared Error')
plt.title('MSE vs Number of Trees in Bagging Regressor')
plt.xscale('log')
plt.grid(True)
plt.show()

References

• Breiman, L. (1996). Bagging predictors. Machine Learning, 24(2), 123-140. Link