Machine learning models, particularly those operating in high-stakes environments such as medical diagnostics, need to offer not just predictions but also a measure of certainty about those predictions. Enter conformal prediction—a powerful, user-friendly approach that provides statistically rigorous confidence measures or intervals for predictions made by virtually any pre-trained model.

Conformal prediction stands out for its ability to generate valid prediction sets without the need for underlying distributional assumptions about the data or the model. This method integrates seamlessly with existing models, including neural networks, and offers guarantees that these prediction sets contain the true outcome with a specified probability. This is crucial in fields where the cost of errors is high, and understanding the degree of uncertainty in predictions can directly impact decision-making processes.

Harnessing Conformal Prediction for Robust Image Classification

Pragmatic Example: Image Classification

Let's begin with a concrete example. Consider a scenario where we have a neural network classifier, denoted as , which is trained to classify images into one of K possible classes. The classifier outputs a softmax score for each class, representing the estimated probability of each class given an input image.

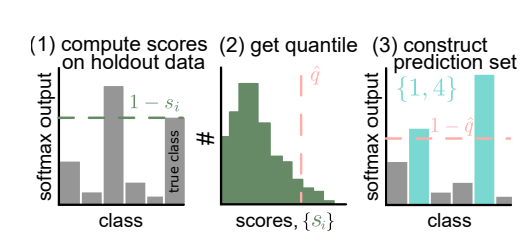
Calibration and Prediction Sets

To improve the reliability of our classifier, we utilize a set of calibration data, which consists of approximately 500 image-class pairs that were not seen during the initial training phase. This calibration step is crucial as it helps adjust and fine-tune our prediction sets.

Formally, the goal is to construct a prediction set for each test image such that the true class of falls within this set with a probability close to a pre-specified confidence level, . This interval is expressed mathematically as:

where n is the number of calibration samples and is the chosen error rate.

Calibration Process:

1. Compute Conformal Scores: First, calculate the conformal score for each calibration sample, defined as , where is the softmax output for the true class of the calibration image . This score is higher when the model's prediction is incorrect or uncertain.

2. Determine Quantile: Define as the empirical quantile of these scores at the level determined by , adjusting for the chosen error rate .

3. Construct Prediction Set: For each new test image , form the prediction set to include all classes y where . This means that any class with a softmax output above this threshold is considered plausible.

Generalization and Interpretation

Conformal prediction is not only limited to image classification. Its principles can be adapted to other machine learning problems, including regression. The flexibility of conformal prediction lies in its ability to produce sets of potential outcomes that are rigorously valid under the model's inherent uncertainties and the unknown distribution of test data.

The size of the prediction set serves as an indicator of the model’s certainty. Larger sets imply greater uncertainty about the image's classification, while smaller sets suggest higher confidence. This adaptive feature of conformal prediction is crucial for practical applications where decision thresholds vary based on the context or the cost of misclassification is high.

Role of Score function

The score function is crucial in conformal prediction, determining the size and effectiveness of the resulting prediction sets. It ranks inputs by the predicted magnitude of error, directly influencing the utility of the prediction sets.

Importance of the Score Function

• Robustness: A strong score function aligns prediction sets with the model's actual performance, enhancing their practical utility.
• Utility: Without a well-designed score function, prediction sets might satisfy statistical coverage criteria but fail to provide actionable insights.

Examples of Score Functions

1. For Classification: 1 - softmax probability of the true class
2. For Regression: Absolute error, |predicted value - actual value|
3. Residual-Based Scores: Using model residuals to dynamically adjust scores based on data statistics.
4. Machine Learning-Driven Scores: Utilizing secondary models to evaluate the reliability of predictions.

Design Considerations

• Model Dependence: The score function should leverage the characteristics of the specific model used.
• Task Relevance: It must be suited to the type of prediction task, whether classification or regression.
• Data Sensitivity: The function should respond to the data distribution and peculiarities.

The design of the score function is crucial, influencing the effectiveness of conformal prediction. Well-constructed score functions ensure that prediction sets are both statistically valid and practically useful.

Code

# 1: get conformal scores. n = calib_Y.shape[0]
cal_smx = model(calib_X).softmax(dim=1).numpy()
cal_scores = 1-cal_smx[np.arange(n),cal_labels]
# 2: get adjusted quantile
q_level = np.ceil((n+1)*(1-alpha))/n
qhat = np.quantile(cal_scores, q_level, method='higher')
val_smx = model(val_X).softmax(dim=1).numpy()
prediction_sets = val_smx >= (1-qhat) # 3: form prediction sets

Applying Conformal Prediction to Regression Tasks

Extending Conformal Prediction to Regression

While conformal prediction has been detailed in the context of image classification, its methodology is equally potent for regression tasks. Regression, which involves predicting continuous variables like house prices or patient health outcomes, benefits greatly from the accuracy and reliability that conformal prediction offers.

The Calibration Process in Regression

The calibration process in regression adapts to handle continuous outcomes. Here’s how it unfolds:

1. Compute Conformal Scores: Use absolute errors between the predicted values and actual values from the calibration data, . Larger scores indicate greater errors.

2. Determine Quantile: Calculate the empirical quantile of these errors, adjusted for the desired confidence level (e.g., 90% confidence would use the 0.1 quantile).

3. Construct Prediction Interval: For new data , construct an interval around the predicted value from to , where is the determined quantile. This interval is expected to contain the actual value with the specified confidence.

Practical Example: Real Estate Pricing

Consider a machine learning model trained to predict real estate prices based on location, size, and number of bedrooms. Using conformal prediction, we can provide prediction intervals that offer a realistic range of possible prices, reflecting the model's reliability.

Code Snippet for Regression

# Load calibration data and model predictions
calibration_predictions = model.predict(calibration_features)
calibration_errors = np.abs(calibration_predictions - calibration_targets)

# Determine the empirical quantile for the desired confidence level
confidence_level = 0.9
quantile = np.quantile(calibration_errors, 1 - confidence_level)

# Predict on new data and form the prediction interval
new_prediction = model.predict(new_features)
prediction_interval = [new_prediction - quantile, new_prediction + quantile]

Advantages in High-Stakes Decisions

In high-stakes environments like finance or healthcare, where the implications of predictions are significant, providing prediction intervals rather than single-point estimates can be crucial. These intervals allow for better risk assessment, offering a safeguard against potential inaccuracies.

Conclusion

Conformal prediction enriches the machine learning toolbox by providing a method that enhances the trust and reliability of model outputs across both classification and regression tasks. By carefully crafting the score function and rigorously applying the calibration process, we ensure that the prediction intervals are meaningful and statistically valid, catering to the nuanced needs of various applications.